Содержание
- 2. Два неравенства f1(x)>g1(x) и f2(x)>g2(x) или два уравнения f1(x) = g1(x) и f2(x) = g2(x) называются
- 3. Неравенства (уравнения) называются равносильными на Х, если множество решений этих неравенств (уравнений) совпадают
- 4. Определение 1. Уравнения, имеющие одно и то же множество корней, называются равносильными
- 5. Например: Уравнения 9x-5=5x+3 и 4x=8 равносильны, так как каждое из них имеет только один корень x=2.
- 6. Из определения равносильности уравнений следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем
- 7. Преобразования уравнений: Любой член уравнения можно переносить из одной части в другую, изменив его знак на
- 8. Однако, не при любом преобразовании уравнение заменяется на равносильное. Например: При возведении в квадрат обеих частей
- 9. Определение 2. Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием
- 10. Из этого определения и определения равносильности уравнений следует: Если два уравнения равносильны, то каждое из них
- 11. Примеры равносильных уравнений и неравенств
- 12. Перенос членов уравнения (неравенства) из одной части в другую Уравнения 4х – 3 = 2х +
- 13. Умножение или деление обеих частей уравнения(неравенства) на одно и то же число ,отличное от нуля. Уравнения
- 14. Замена части уравнения (неравенства) тождественно равным ему выражением Уравнения х2 +3х = 0 и х (х+3)
- 15. Решить уравнение √х = х – 2 (1) х = (х – 2)2 (2) х =
- 16. Установить, какое из двух уравнений является следствием другого уравнения
- 18. Скачать презентацию















 Л.10_Непрерывность функции
Л.10_Непрерывность функции Основное свойство дроби
Основное свойство дроби 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Происхождение неевклидовой геометрии
Происхождение неевклидовой геометрии Сложение и вычитание в пределах первого десятка. Интерактивная игра-соревнование Поиграем в баскетбол
Сложение и вычитание в пределах первого десятка. Интерактивная игра-соревнование Поиграем в баскетбол Теория пределов. Лекция 4
Теория пределов. Лекция 4 Презентация на тему Решение уравнений и неравенств, содержащих модуль
Презентация на тему Решение уравнений и неравенств, содержащих модуль  Сложение и вычитание чисел в пределах 20
Сложение и вычитание чисел в пределах 20 Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения Что? Где? Когда?
Что? Где? Когда? Урок-игра: Геометрические состязания
Урок-игра: Геометрические состязания Математический тренажер. Двузначное число
Математический тренажер. Двузначное число Презентация на тему Параллелограмм. Свойства параллелограмма
Презентация на тему Параллелограмм. Свойства параллелограмма  Презентация на тему Нужна ли в жизни координатная плоскость
Презентация на тему Нужна ли в жизни координатная плоскость  Виды треугольников
Виды треугольников Рототабельное планирование
Рототабельное планирование История появления тригонометрии
История появления тригонометрии Практика. Дискретная математика
Практика. Дискретная математика Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Решение систем неравенств первой степени с одним неизвестным
Решение систем неравенств первой степени с одним неизвестным Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7 Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Свойства функции (10 класс)
Свойства функции (10 класс) Результант. Литература
Результант. Литература Презентация на тему Понятие угла
Презентация на тему Понятие угла 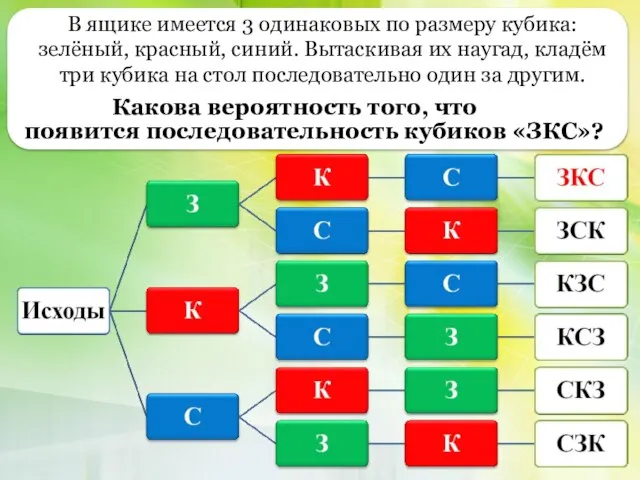 Решение вероятностных задач с помощью комбинаторики. 3-й вид задач
Решение вероятностных задач с помощью комбинаторики. 3-й вид задач Определенный интеграл. Формула
Определенный интеграл. Формула