Содержание
- 2. Плоскость, параллельная плоскости основания пирамиды и пересекающая пирамиду, отсекает от нее подобную пирамиду. Другая часть пирамиды
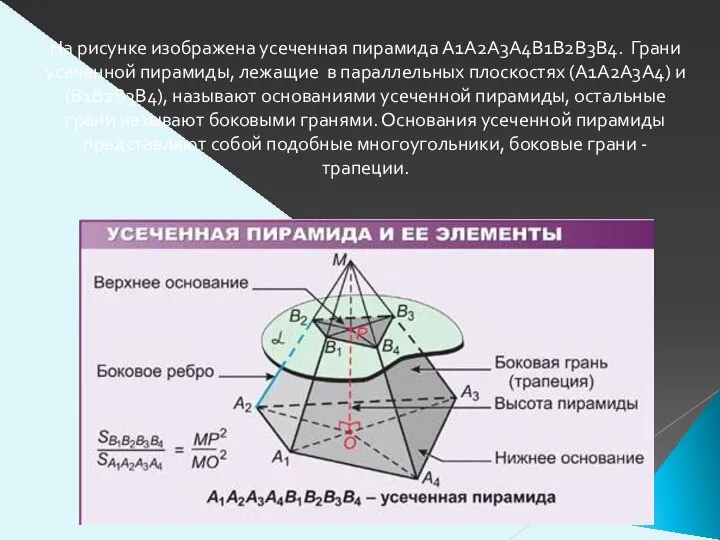
- 3. На рисунке изображена усеченная пирамида A1А2А3А4В1В2В3В4. Грани усеченной пирамиды, лежащие в параллельных плоскостях (A1А2А3А4) и (B1В2В3В4),
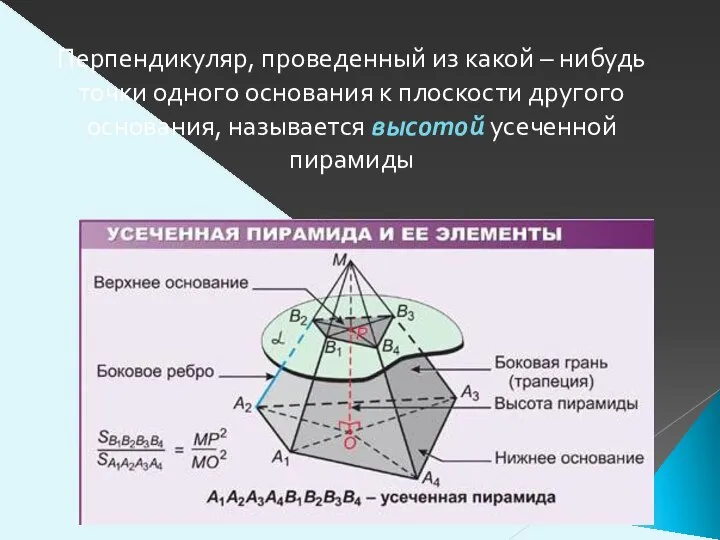
- 4. Перпендикуляр, проведенный из какой – нибудь точки одного основания к плоскости другого основания, называется высотой усеченной
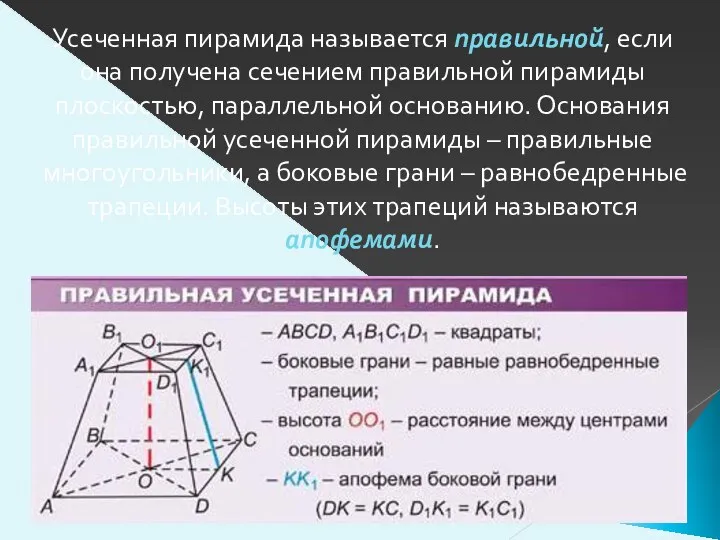
- 5. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной
- 6. Правильная усеченная пирамида также как и обычная правильная пирамида имеет особенности: В правильной усеченной n-угольной пирамиде
- 7. Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему S бок=½(P+P´)
- 9. Скачать презентацию



 Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Исследование функции с помощью производной и построение графика функции
Исследование функции с помощью производной и построение графика функции Акула. Примеры
Акула. Примеры Линейная функция
Линейная функция Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Презентация на тему Наибольший общий делитель, наименьшее общее кратное
Презентация на тему Наибольший общий делитель, наименьшее общее кратное  Построение графика функции
Построение графика функции Математическая раскраска
Математическая раскраска Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Математические приемы быстрого счета (лайфхаки)
Математические приемы быстрого счета (лайфхаки) Цикломатика графов
Цикломатика графов Профильная математика № 17
Профильная математика № 17 Производная степенной функции. Производная и её геометрический смысл
Производная степенной функции. Производная и её геометрический смысл Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Эволюционные этапы развития логистики
Эволюционные этапы развития логистики Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)
Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)  Аксиомы стереометрии
Аксиомы стереометрии Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Определитель второго порядка
Определитель второго порядка Пропорциональность величин
Пропорциональность величин Построение графика функции
Построение графика функции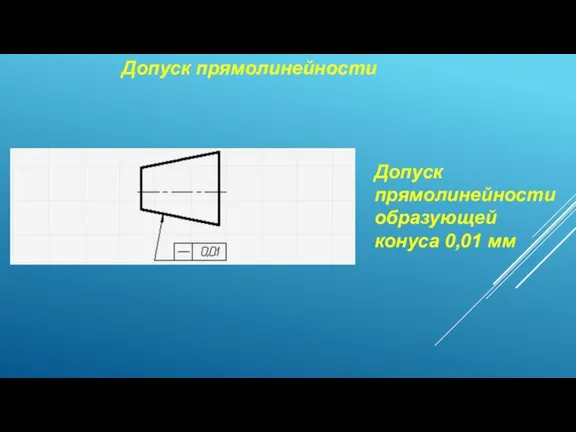 Допуск прямолинейности
Допуск прямолинейности Множення і ділення десяткових дробів. 5 клас
Множення і ділення десяткових дробів. 5 клас Что такое проекция вектора
Что такое проекция вектора У гостях у Цвіріньчика
У гостях у Цвіріньчика Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1)