Содержание
- 2. Содержание 1. Определение модуля 2. Виды уравнений 3. Методы решения уравнений 4. Задания для самостоятельного решения
- 3. Большинство уравнений с модулем можно решить исходя из определения модуля: Модулем или абсолютной величиной действи-тельного числа
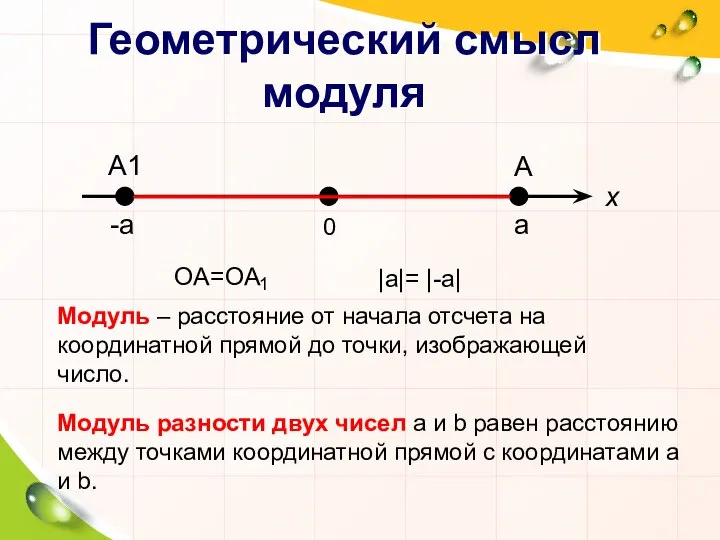
- 4. Геометрический смысл модуля -a a 0 A1 A x Модуль – расстояние от начала отсчета на
- 5. 1. |a|≥0 2. |a| = | − a|; 3.|a| ≥ a и |a| ≥ −a; или
- 6. Из определения и свойств модуля вытекают основные методы решения уравнений и неравенств с модулем: “раскрытие” модуля
- 7. Уравнение вида: Равносильно : МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ.
- 8. Заметим, что если бы мы решали уравнение по определению, то у нас возникли бы затруднения при
- 9. Такие уравнения можно решать двумя способами: I способ: Если f(x) имеет более простой вид, чем g(x),
- 10. Пример 2 Решение: Решить уравнение
- 11. Решим уравнение второй системы: Решим уравнение первой системы:
- 12. Вернемся к совокупности систем: Ответ:
- 13. II способ: Если g(x) имеет более простой вид, чем f(x). Если g(x) Если g(x)≥0, то
- 14. Решим первое уравнение совокупности: Пример 3 Решение: Решить уравнение
- 15. Решим второе уравнение совокупности: Вернемся к системе: Система решений не имеет, следовательно, уравнение решений не имеет.
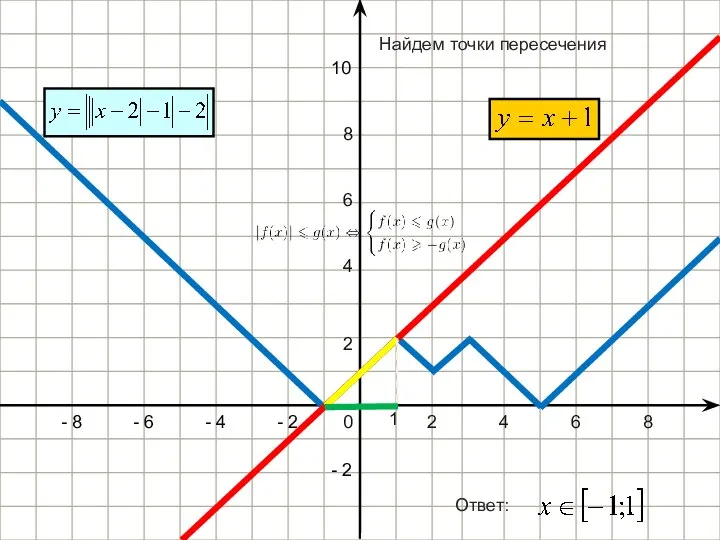
- 16. Так как обе части уравнения неотрицательны, то Рассмотрим уравнения вида И мы получаем следующую равносильность:
- 17. Решим первое уравнение совокупности: Пример 4 Решение: Решить уравнение
- 18. Решим второе уравнение совокупности: Ответ: Вернемся к совокупности:
- 19. Для решения уравнений такого вида удобно воспользоваться следующим алгоритмом: Найти нули подмодульных выражений; Провести столько параллельных
- 20. Пример 5 Решение: Решить уравнение -3 -1 2
- 21. Раскрывая модули на каждом интервале, получим совокупность систем: Ответ: -2; 8
- 22. В некоторых случаях удобнее использовать метод замены переменной. Пример 6 Решение: Ответ: Решить уравнение Данное уравнение
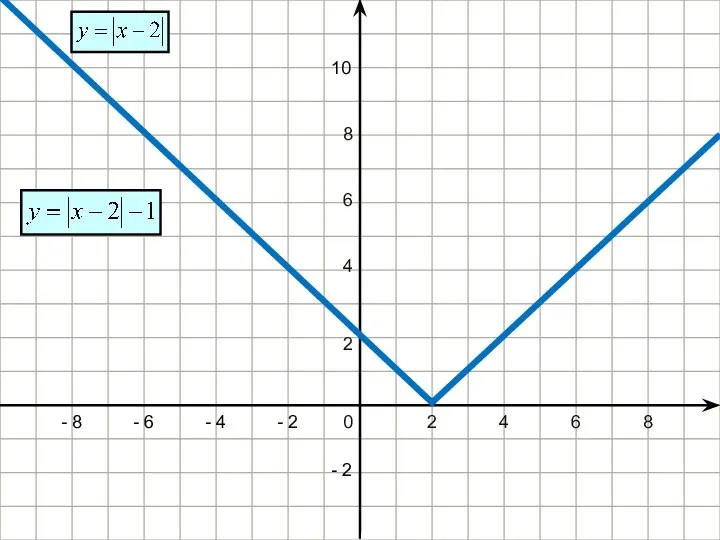
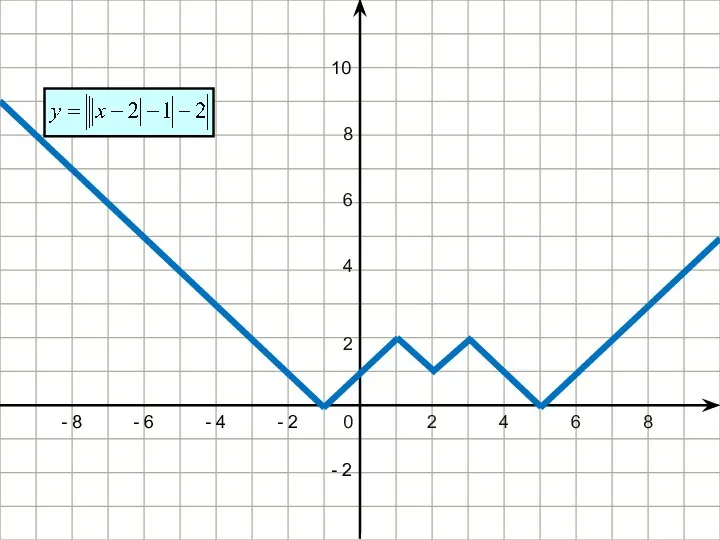
- 23. Бывает и так , что уравнение нельзя отнести ни к одному из рассмотренных типов, а так
- 24. 2 4 6 8 - 2 - 4 - 6 - 8 - 2 4 6
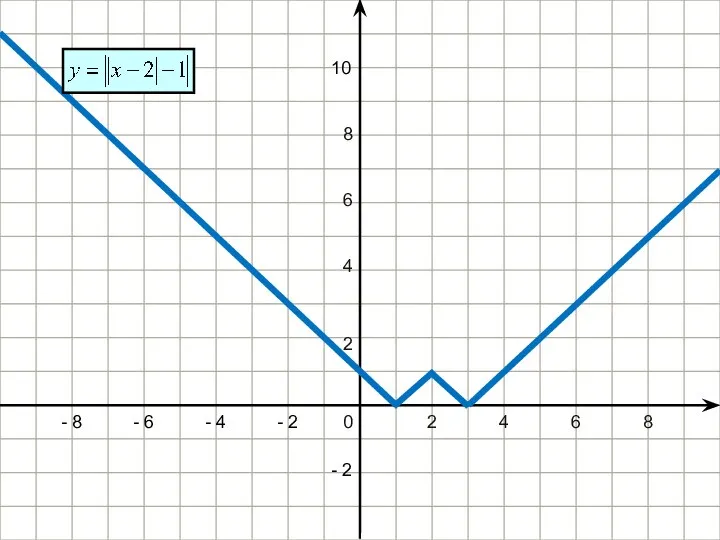
- 25. 2 4 6 8 - 2 - 4 - 6 - 8 - 2 4 6
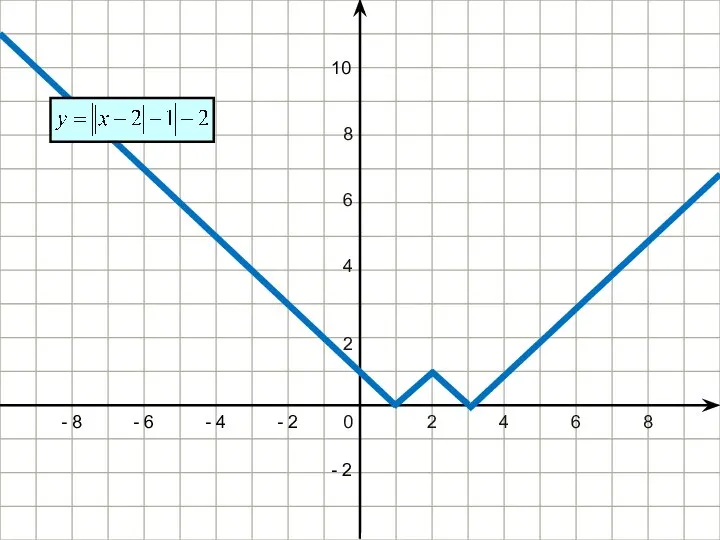
- 26. 2 4 6 8 - 2 - 4 - 6 - 8 - 2 4 6
- 27. 2 4 6 8 - 2 - 4 - 6 - 8 - 2 4 6
- 28. 2 4 6 8 - 2 - 4 - 6 - 8 - 2 4 6
- 29. Задания для самостоятельного решения:
- 30. Выводы 1. Виды уравнений: 2. Методы решения уравнений Аналитический: - по определению - использование равносильности -
- 32. Скачать презентацию























 Окружность. Вписанные и описанные углы
Окружность. Вписанные и описанные углы Матрицы
Матрицы Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Симметрия в окружающем нас мире
Симметрия в окружающем нас мире Площадь четырехугольника
Площадь четырехугольника Составление объемных фигур из отдельных элементов кубиков Сома
Составление объемных фигур из отдельных элементов кубиков Сома Перестановки. Размещения
Перестановки. Размещения chislo-pi
chislo-pi В мире чисел и цифр
В мире чисел и цифр ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тренировочные задания В2 (графическое представление данных)
Тренировочные задания В2 (графическое представление данных) Элементы комбинаторики
Элементы комбинаторики Подготовка к ГИА. Задачи
Подготовка к ГИА. Задачи Касательная к окружности
Касательная к окружности Расчет нормированных приоритетов
Расчет нормированных приоритетов Приемы письменных вычислений
Приемы письменных вычислений Векторы. Обобщающий урок
Векторы. Обобщающий урок Величины и их измерение. Длина
Величины и их измерение. Длина Понятие цилиндра
Понятие цилиндра Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Лекция 2
Лекция 2 Презентация Понономарев
Презентация Понономарев Геометрия (8 класс)
Геометрия (8 класс) Статистика и дизайн информации
Статистика и дизайн информации Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Определители матриц
Определители матриц Письмо от президента Клуба серьёзных математиков
Письмо от президента Клуба серьёзных математиков