Содержание
- 2. Понятие выборки Выборка – это последовательность наблюдений. Это могут быть наблюдения любой природы: некоторой физической величины
- 3. Характеристики выборки Среднее значение: Это наиболее распространенная характеристика центра выборки. Обычно, когда говорят «средний», подразумевают «типичный»,
- 4. Характеристики выборки Медиана (от лат. mediāna — середина). Медиана — это такое число, что половина из
- 5. Характеристики выборки Предположим, что в одной комнате оказалось 19 бедняков и один миллионер. У каждого бедняка
- 6. Характеристики выборки Мода — значение во множестве наблюдений, которое встречается наиболее часто. Таким образом, мода –
- 7. Характеристики рассеяния, разброса, изменения выборки Размах: R=xmax-xmin Не самая лучшая характеристика рассеяния выборки. Например, Она одинакова
- 8. Выборочная дисперсия: Характеристики рассеяния, разброса, изменения выборки Дисперсия характеризует среднее отклонение (разброс, рассеяние, изменение, вариацию) наблюдений
- 9. В теории вероятностей доказывается формула: Характеристики рассеяния, разброса, изменения выборки Если использовать обозначения, принятые в лекции
- 10. Единицы измерения Dx – это единицы измерения x в квадрате. Чтобы рассеяние измерялось в тех же
- 11. Зависимость двух выборок Пусть мы проводим наблюдения так, что в одном наблюдении определяем сразу два параметра
- 12. Числовые характеристики зависимости двух выборок Выборочная ковариация выборок x и y: Из теории вероятностей известно: если
- 13. В теории вероятностей доказывается формула: Если использовать обозначения, принятые в лекции 9 (слайд 9), то получим:
- 14. Величина Kx,y зависит от единиц измерения x и y. Например, пусть x – рост человека, и
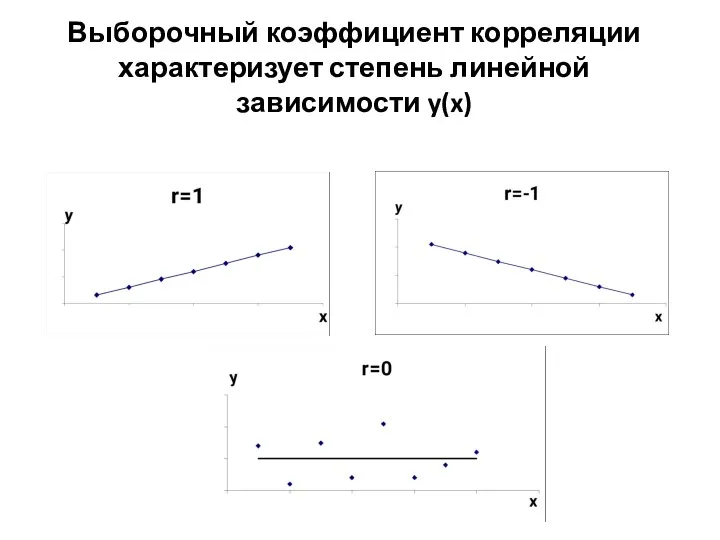
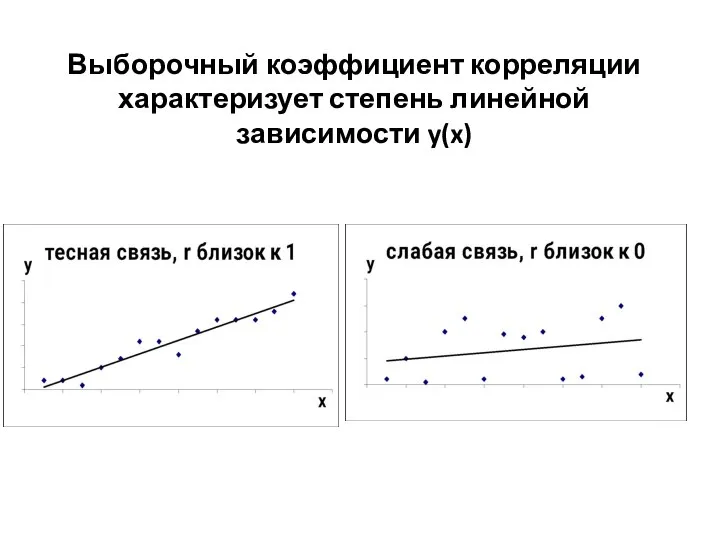
- 15. Свойства выборочного коэффициента корреляции (доказываются в теории вероятностей): -1≤r≤1. Чем ближе ⏐r⏐ к 1, тем сильнее
- 16. Выборочный коэффициент корреляции характеризует степень линейной зависимости y(x)
- 17. Выборочный коэффициент корреляции характеризует степень линейной зависимости y(x)
- 18. Определение параметров функции y=mx+b по наблюдениям ее значений методом наименьших квадратов Вспомним формулу для оценок параметров
- 19. Определение параметров функции y=mx+b по наблюдениям ее значений методом наименьших квадратов Из формул (2), (4) и
- 20. Встроенные функции Matlab для вычисления характеристик выборок mean (x) – возвращает среднее значение выборки; median(x) –
- 22. Скачать презентацию

















 Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Веселый паровоз. Мультимедийное пособие по математике
Веселый паровоз. Мультимедийное пособие по математике Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел 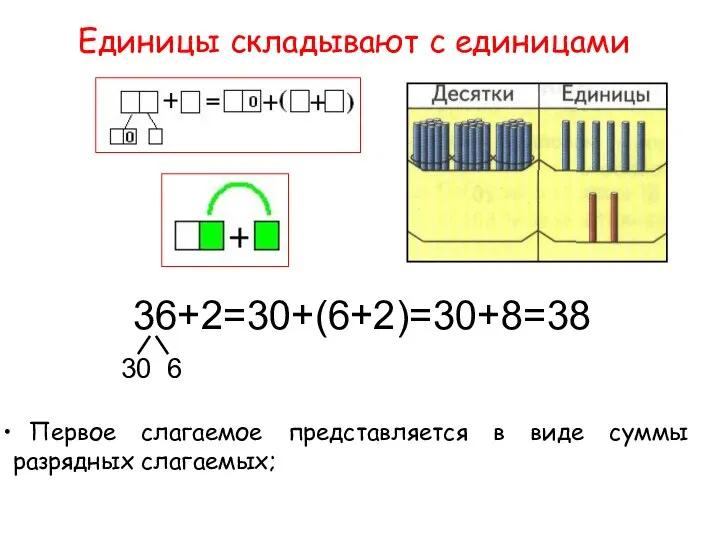 Алгоритм вычислений
Алгоритм вычислений Логика
Логика Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Пирамида. Виды пирамид
Пирамида. Виды пирамид Игра-тренажёр Округление чисел
Игра-тренажёр Округление чисел Вычисление одномерных, двумерных и интегралов c переменным верхним пределом
Вычисление одномерных, двумерных и интегралов c переменным верхним пределом Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) Правильные многогранники
Правильные многогранники Алгебраические выражения
Алгебраические выражения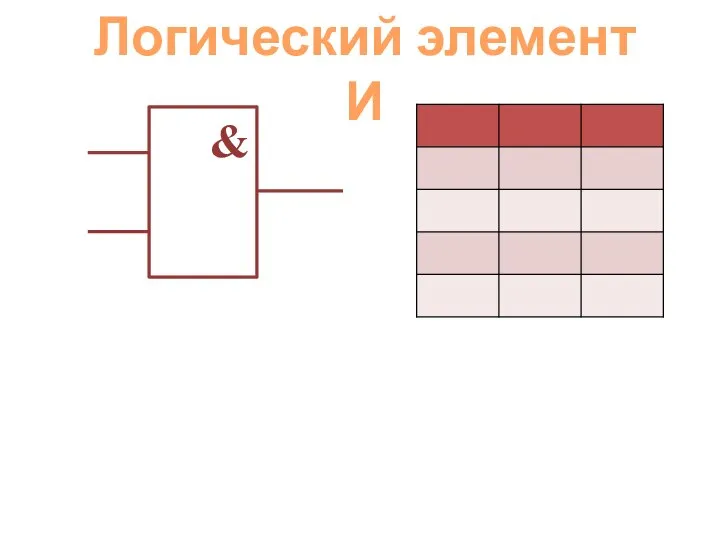 Логический элемент
Логический элемент Презентация на тему Вектор
Презентация на тему Вектор  Правила с двумя решениями. Подход Неймана – Пирсона
Правила с двумя решениями. Подход Неймана – Пирсона Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2» Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Окружность. 5 класс
Окружность. 5 класс Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)
Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс) Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013