Содержание
- 2. Понятие вектора Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом,
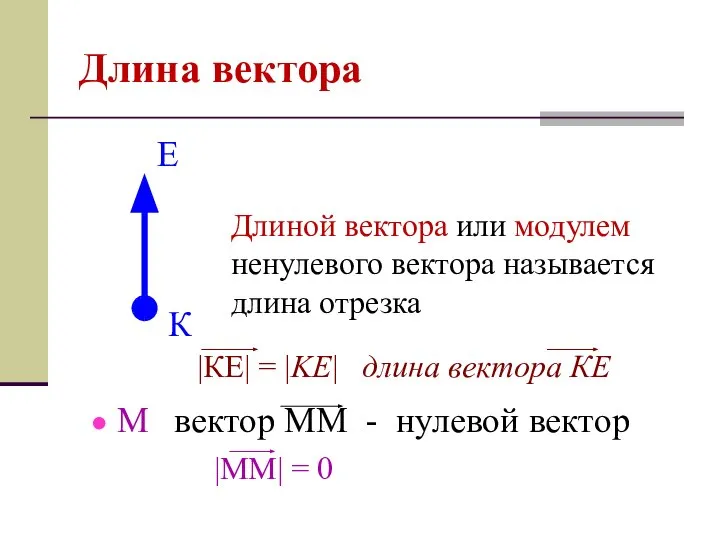
- 3. Длина вектора Длиной вектора или модулем ненулевого вектора называется длина отрезка
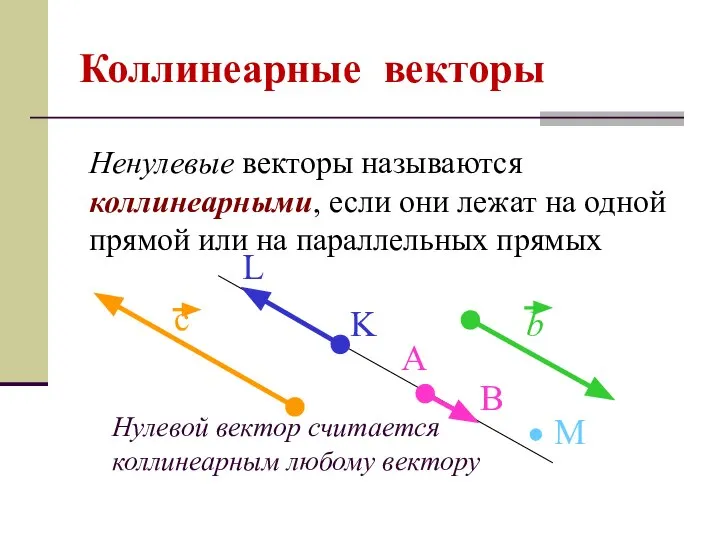
- 4. Нулевой вектор считается коллинеарным любому вектору Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат на
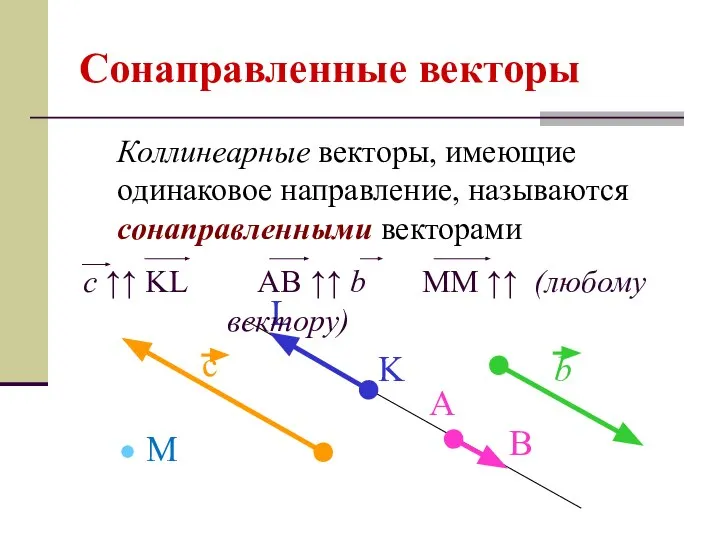
- 5. Сонаправленные векторы Коллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
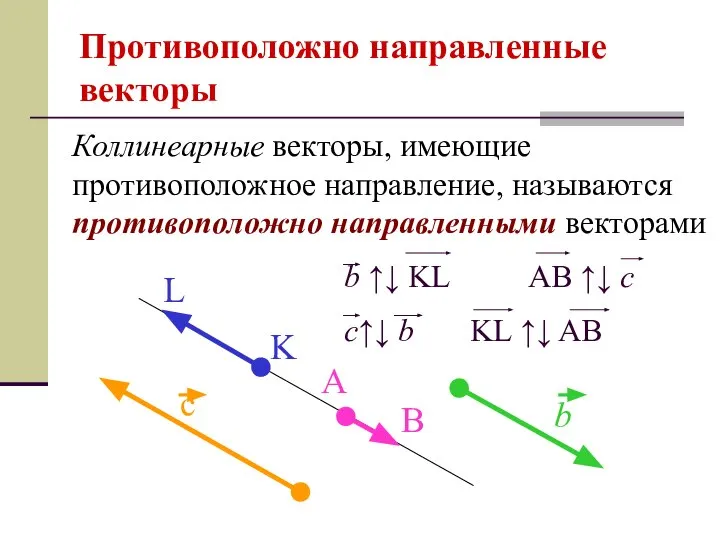
- 6. Противоположно направленные векторы Коллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
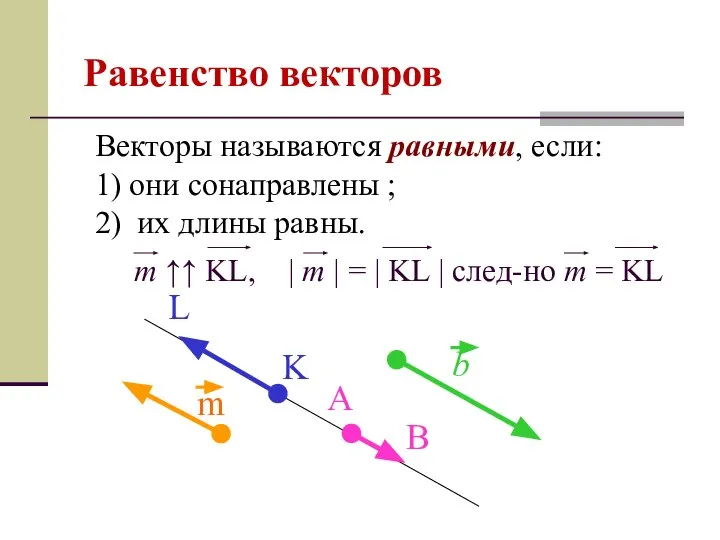
- 7. Равенство векторов Векторы называются равными, если: 1) они сонаправлены ; 2) их длины равны. m
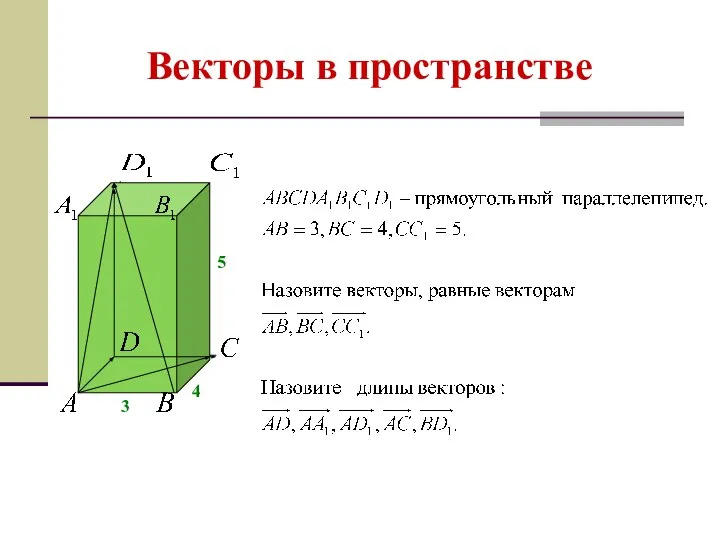
- 8. Векторы в пространстве
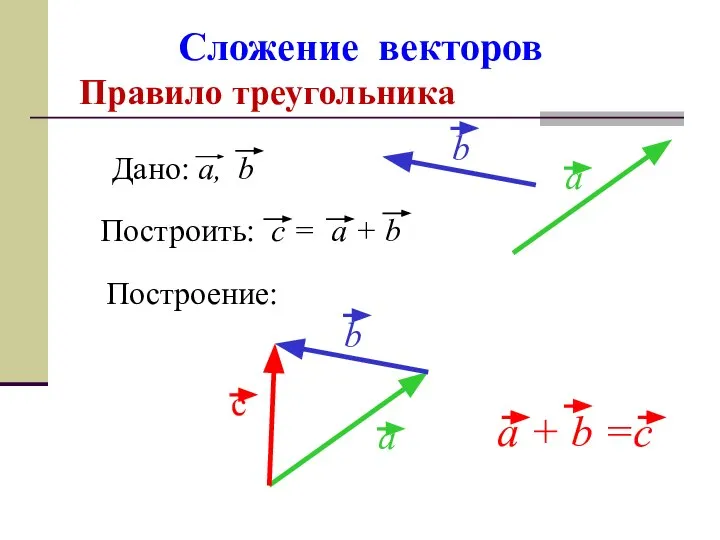
- 9. Сложение векторов Правило треугольника Построение:
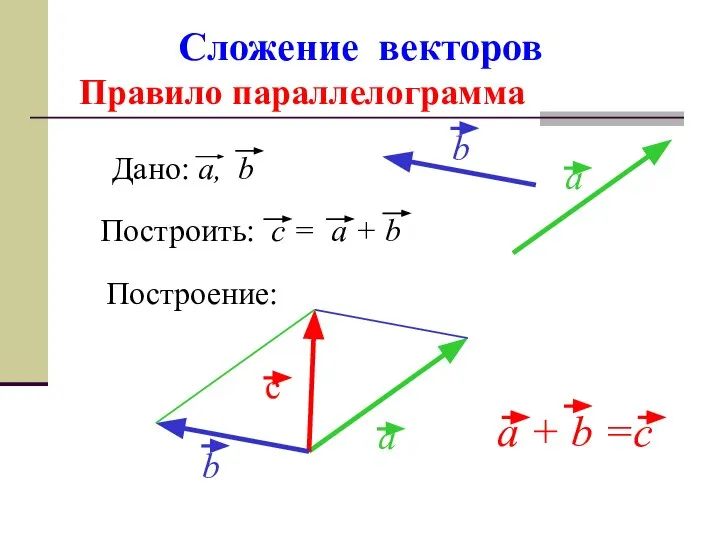
- 10. Сложение векторов Правило параллелограмма Построение:
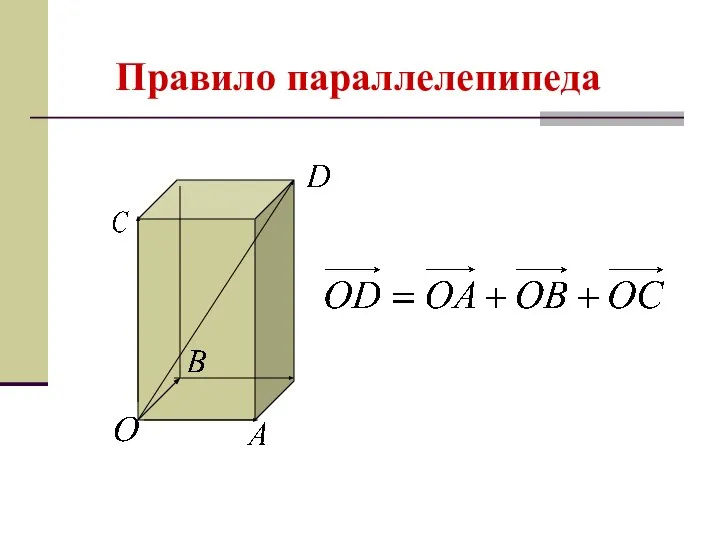
- 11. Правило параллелепипеда
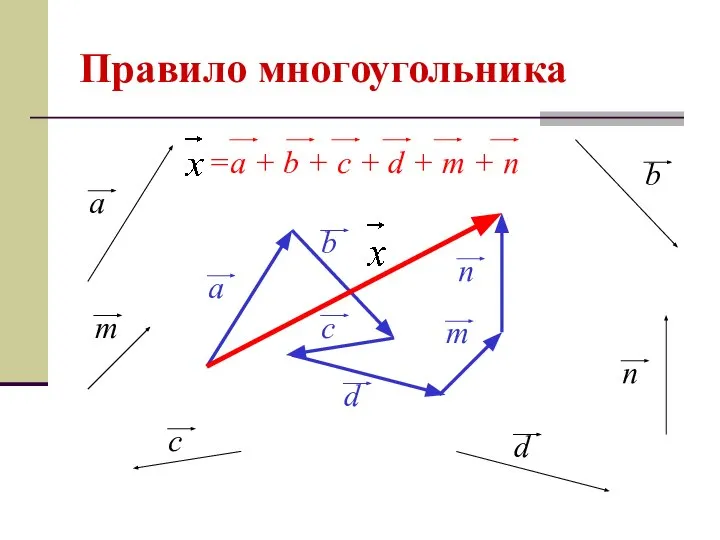
- 12. Правило многоугольника
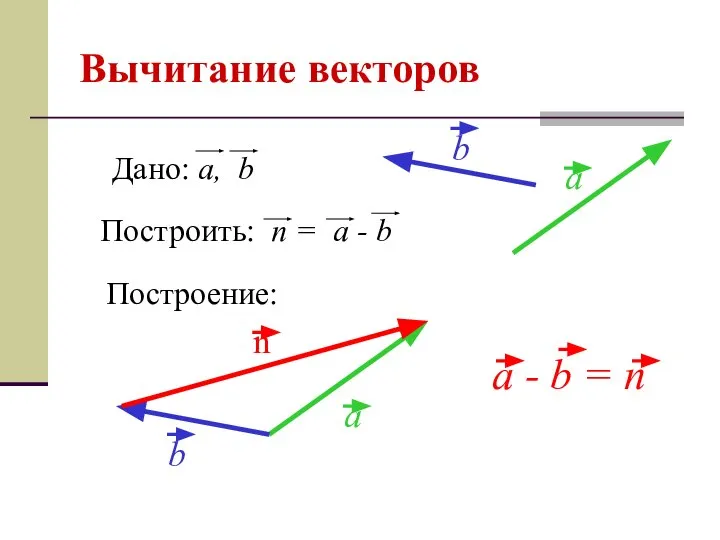
- 13. Вычитание векторов Построение:
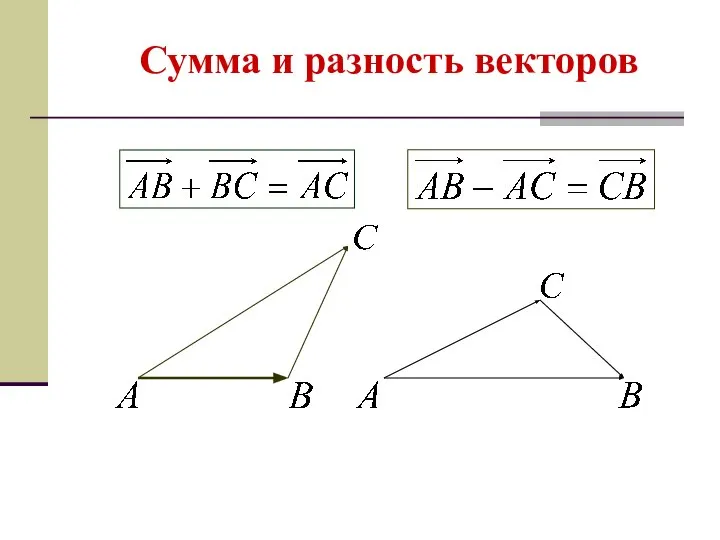
- 14. Сумма и разность векторов
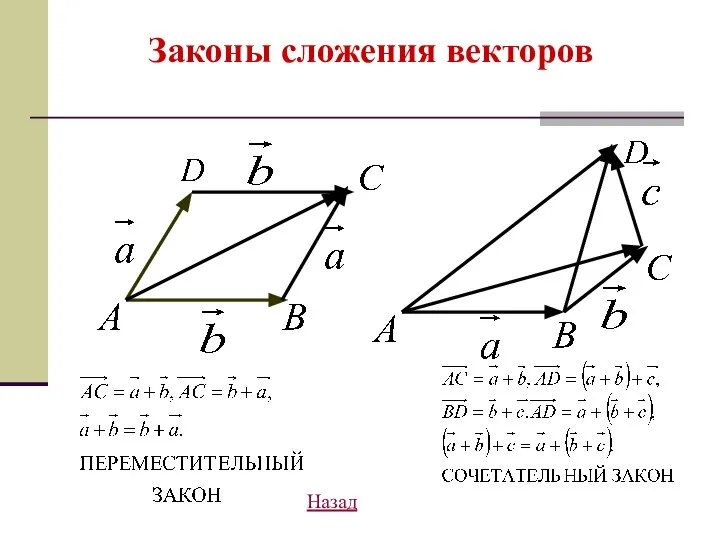
- 15. Законы сложения векторов Назад
- 16. Умножение вектора a на число k k·a = b, |a| ≠ 0, k – произвольное число
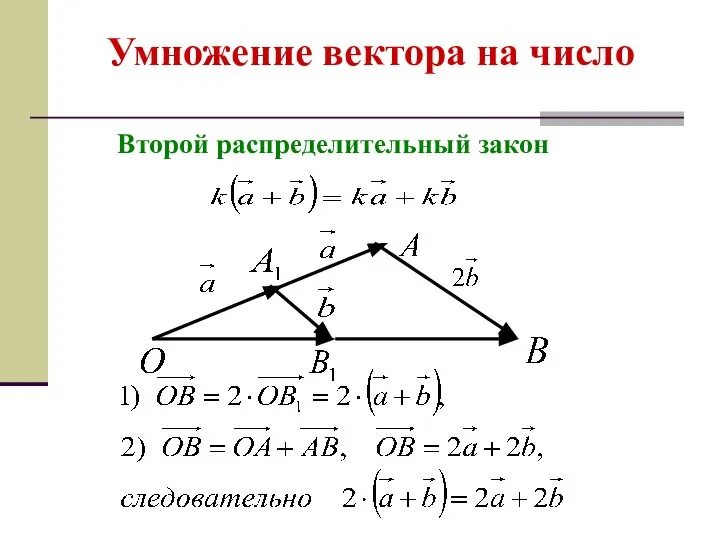
- 17. Умножение вектора на число
- 18. Умножение вектора на число
- 19. Умножение вектора на число
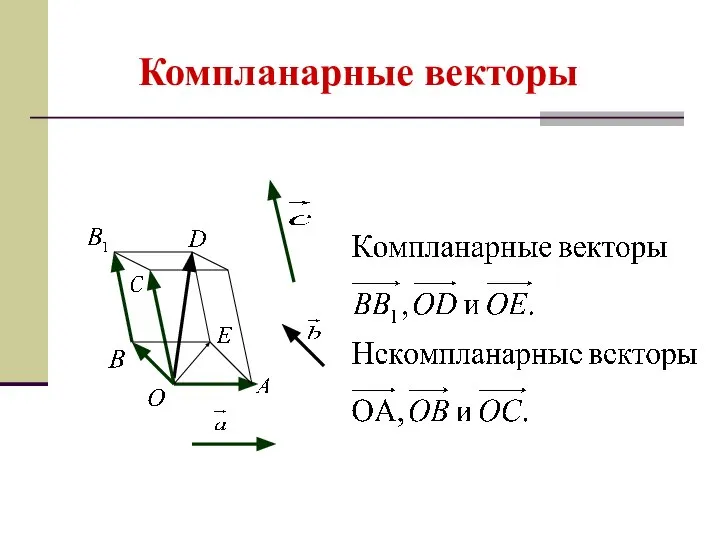
- 20. Компланарные векторы Векторы называются компланарными, если при откладывании их от одной точки они будут лежать в
- 21. Компланарные векторы
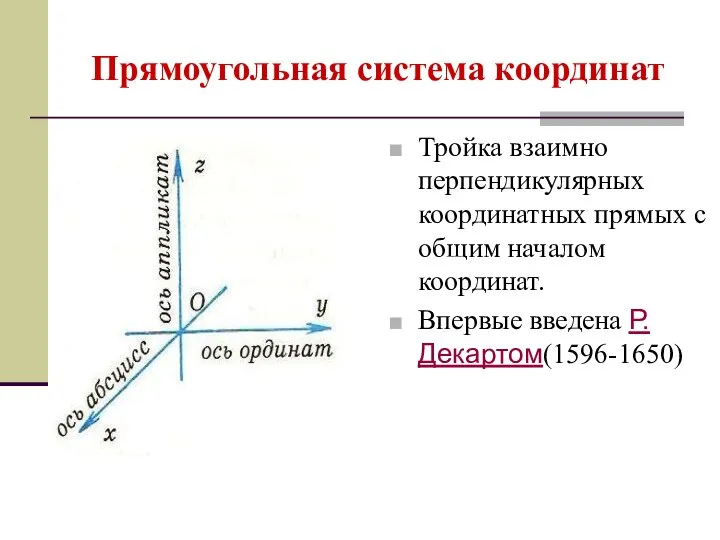
- 22. Прямоугольная система координат Тройка взаимно перпендикулярных координатных прямых с общим началом координат. Впервые введена Р.Декартом(1596-1650)
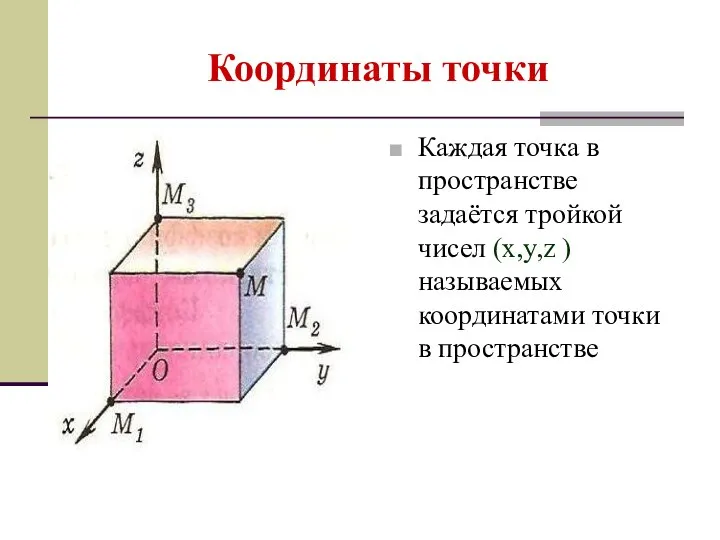
- 23. Координаты точки Каждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых координатами точки в пространстве
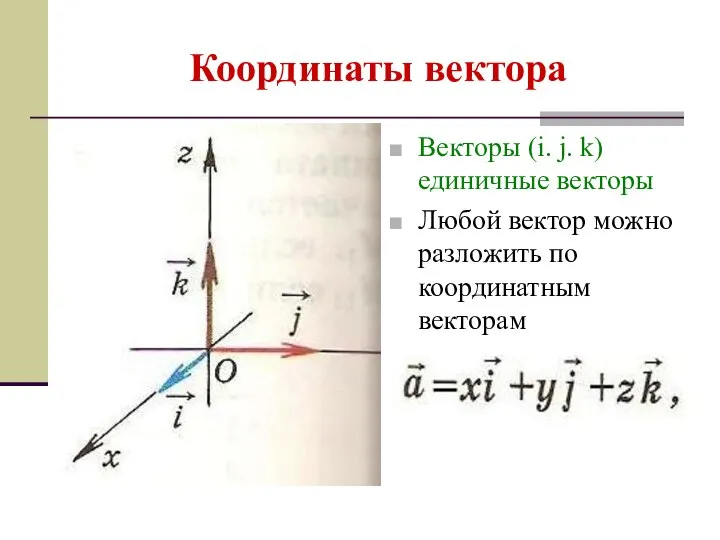
- 24. Координаты вектора Векторы (i. j. k) единичные векторы Любой вектор можно разложить по координатным векторам
- 25. Длина вектора
- 26. Скалярное произведение векторов
- 28. Скачать презентацию







 Решение задач ЕГЭ по тригонометрии
Решение задач ЕГЭ по тригонометрии Движения
Движения Виды векторов
Виды векторов Тренажёр Яблоки по теме Сложение с переходом через десяток. 1 класс
Тренажёр Яблоки по теме Сложение с переходом через десяток. 1 класс Статистика знает всё
Статистика знает всё Решение заданий №17 ЕГЭ профильной математики (задания с параметром)
Решение заданий №17 ЕГЭ профильной математики (задания с параметром) Самостоятельная работа. Геометрия
Самостоятельная работа. Геометрия Первый признак равенства треугольников
Первый признак равенства треугольников Системы линейных уравнений. Метод Гаусса
Системы линейных уравнений. Метод Гаусса Урок геометрии в 7 классе Искусство рассуждать
Урок геометрии в 7 классе Искусство рассуждать Швидкість вітру у вільній атмосфері
Швидкість вітру у вільній атмосфері Модуль числа
Модуль числа Урок-экскурсия по Родному краю
Урок-экскурсия по Родному краю Презентация на тему Десятичные дроби (6 класс)
Презентация на тему Десятичные дроби (6 класс)  Практическое применение подобия треугольников
Практическое применение подобия треугольников Решение задач с помощью уравнений
Решение задач с помощью уравнений Реализация статистических методов оценки параметров динамической случайной величины
Реализация статистических методов оценки параметров динамической случайной величины Производная и первообразная
Производная и первообразная Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Число и цифра 2
Число и цифра 2 Геометрия египетских пирамид
Геометрия египетских пирамид Презентация на тему Проценты 5 класс
Презентация на тему Проценты 5 класс  Число и цифра 9
Число и цифра 9 Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Возведение в степень. Куб и квадрат числа
Возведение в степень. Куб и квадрат числа Лабораторная работа №2. Вычисление геодезических координат по прямоугольным координатам Гаусса-Крюгера
Лабораторная работа №2. Вычисление геодезических координат по прямоугольным координатам Гаусса-Крюгера Задача по математике (1 класс, задание 13.2)
Задача по математике (1 класс, задание 13.2) Геометрический смысл производной
Геометрический смысл производной