Содержание
- 2. А. Нивен Математику нельзя изучать, наблюдая как это делает сосед. А. Нивен
- 3. Запомним Решить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств
- 4. Запомним Если надо решить систему неравенств, то: решаем каждое неравенство системы отдельно изображаем полученные решения на
- 5. Содержание Решение систем линейных неравенств Решение двойных неравенств Решение систем, содержащих квадратные неравенства
- 6. Решим систему неравенств (состоящую из линейных неравенств) 5х + 1 > 6 2х – 4 Решение:
- 7. Решим систему неравенств 5х + 12 ≤ 3х+ 20 х 2х + 7 ≥ 0 Решение:
- 8. Работа в парах: Решить систему неравенств: 1) 3х – 2 ≥ х + 1 4 –
- 9. Примеры двойных неравенств Прочитайте неравенства: -6 -1,2 ≤ х 0
- 10. Решение двойных неравенств Решить неравенство: 0 Решение: составим систему: 4х + 2 > 0 4х +
- 11. Решите неравенства, работая в парах Решить неравенства: -6 ≤ - 3х ≤ 3 4 -2 ≤
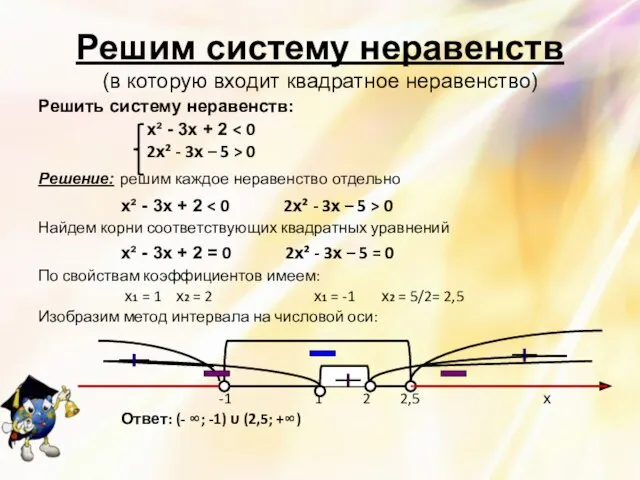
- 12. Решим систему неравенств (в которую входит квадратное неравенство) Решить систему неравенств: х² - 5х + 4
- 13. Решить систему неравенств: х² - 3х + 2 2х² - 3х – 5 > 0 Решение:
- 14. Решим системы неравенств, работая вместе 1) 6х² - 5х + 1 > 0 4х – 1
- 15. Решите системы неравенств, работая самостоятельно 1) х² - 10х + 9 ≥ 0 12 – 3х
- 17. Скачать презентацию













 Векторы. 9 класс
Векторы. 9 класс Формула объема пирамиды
Формула объема пирамиды Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Все действия с рациональными дробями. Подготовка к контрольной работе
Все действия с рациональными дробями. Подготовка к контрольной работе Формула у=х2
Формула у=х2 Многочлен. Стандартный вид многочлена. Степень многочлена
Многочлен. Стандартный вид многочлена. Степень многочлена Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Геометрия. Построение
Геометрия. Построение Евклидова геометрия
Евклидова геометрия Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем Измерение площади с помощью палетки. 4 класс
Измерение площади с помощью палетки. 4 класс Вторая производная и ее физический смысл
Вторая производная и ее физический смысл Отношения и пропорция
Отношения и пропорция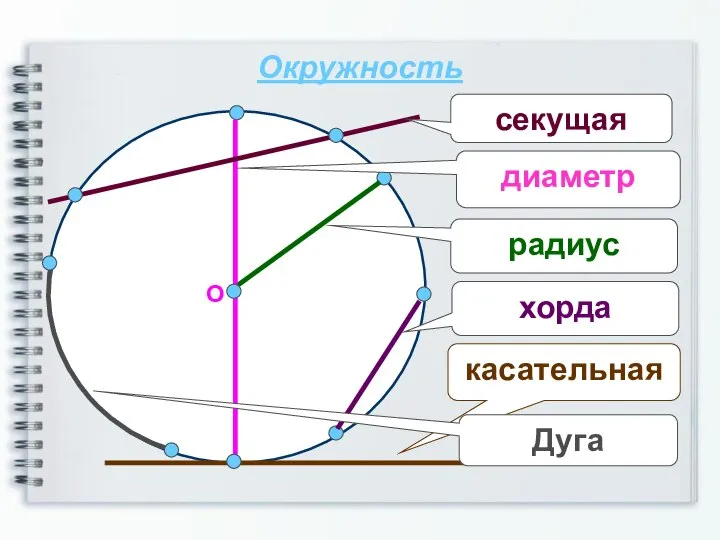 Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1)
Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1) Теорема о площади треугольников
Теорема о площади треугольников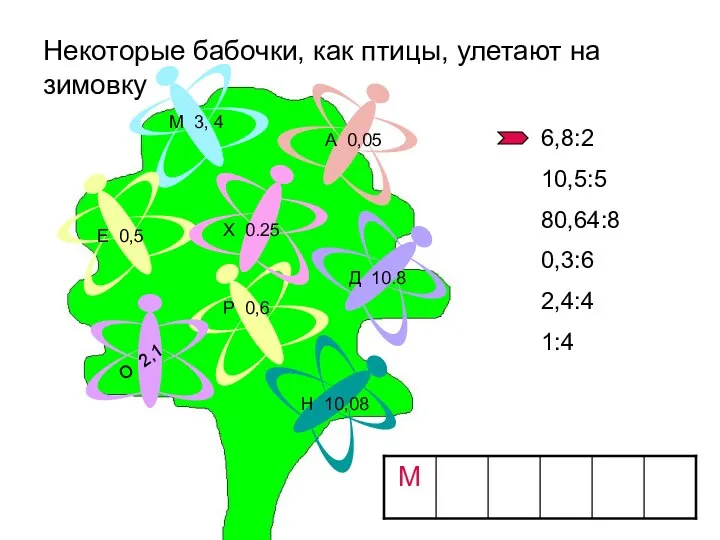 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Тела вращения. Урок 142
Тела вращения. Урок 142 Веселая математика. Головоломки
Веселая математика. Головоломки Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Методы расчета КИХ-фильтров
Методы расчета КИХ-фильтров Коррекция нелинейных систем
Коррекция нелинейных систем Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са
Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са Решение неполных квадратных уравнений
Решение неполных квадратных уравнений Планирование эксперимента
Планирование эксперимента Консультация ДУ
Консультация ДУ