Слайд 2 Числові функції
Якщо кожному значенню змінної Х з деякої множини D

відповідає єдине значення змінної У, то таку відповідність називають функцією.
При цьому Х називають незалежною змінною, або аргументом, У – залежною змінною, або функцією.
Слайд 3
Аналітичний або за допомогою формули
y = x – 2; y

= (x + 10)/x.
За таблицею
Графіком
Словесний спосіб
Способи задання функції
Слайд 4 Дослідження функції
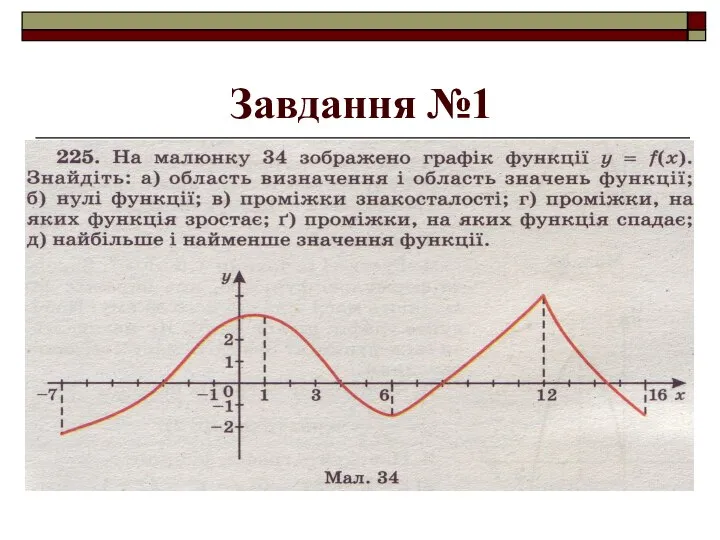
Дослідити функцію – це означає виявити її найважливіші властивості:
1)

вказати область визначення;
2) вказати область значень;
3) з'ясувати, чи є дана функція парною або непарною;
4) знайти точку перетину графіка функції з віссю У;
5) знайти нулі функції та проміжки знакосталості;
6) визначити проміжки зростання чи спадання функції.
Узагальнивши все, слід побудувати графік функції.
Слайд 5 Властивості функції
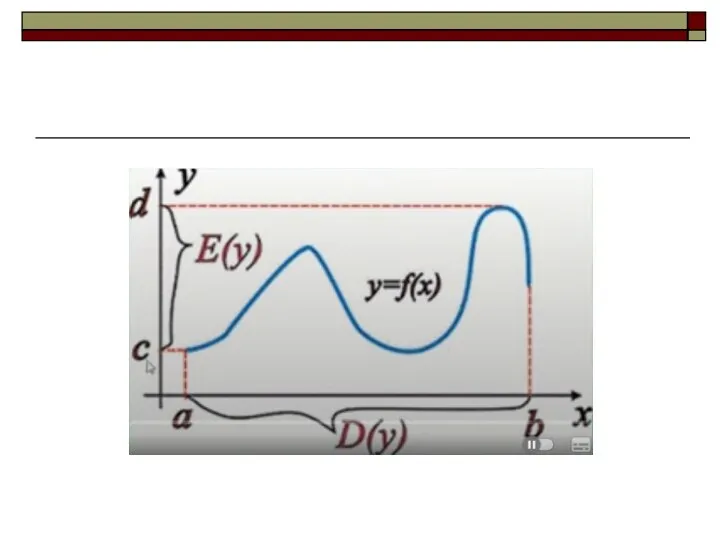
Усі значення, які може набувати аргумент функції, називають областю визначення

даної функції і позначають літерою D.
Множину всіх значень у, яких може набувати функція, називають її областю значень і позначають літерою Е.
Слайд 7 Види функцій, їх області визначення
та множини значень

Слайд 8 Парність
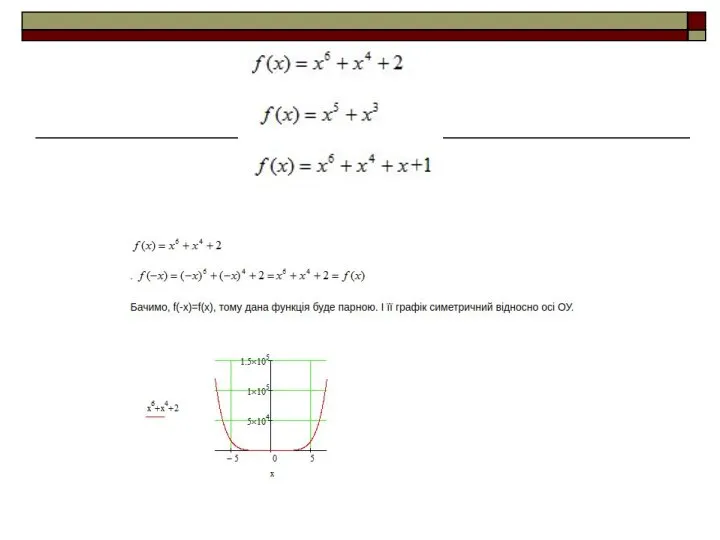
Функція y = f (x) називається парною, якщо її область

визначення симетрична відносно нуля і для кожного значення х з області визначення f(-x) = f(x).
Графік парної функції симетричний відносно осі У.
Функція y = f (x) називається непарною, якщо її область визначення симетрична відносно нуля і для кожного значення х із області визначення f(-x) = - f(x).
Графік непарної функції симетричний відносно початку координат.
Слайд 13 Нулі функції та проміжки
знакосталості
Значення аргументу, при яких значення функції

дорівнює нулю, називають нулями функції. Щоб знайти нулі функції y = f (x), потрібно розв'язати рівняння f (x) = 0.
Проміжки області визначення функції, на яких функція не змінює знака (тобто має тільки додатні або тільки від'ємні значення), називають проміжками знакосталості. Щоб знайти проміжки знакосталості, потрібно розв'язати нерівності f (x)>0 і f (x)<0. Розв’язки нерівності f (x)>0 – це значення аргументу, при яких функція набуває додатних значень.
Слайд 14 Монотонність
Функцію називають зростаючою на деякому проміжку, якщо кожному більшому значенню аргументу

із цього проміжку відповідає більше значення функції.
Функцію називають спадною на деякому проміжку, якщо кожному більшому значенню аргументу із цього проміжку відповідає менше значення функції.
Якщо функція на всій області визначення зростає або на всій області визначення спадає, її називають монотонною.
Слайд 15 Неперервність
Якщо графіком функції є неперервна лінія (її можна провести, не

відриваючи олівець від паперу), то таку функцію називають неперервною функцією.















 Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів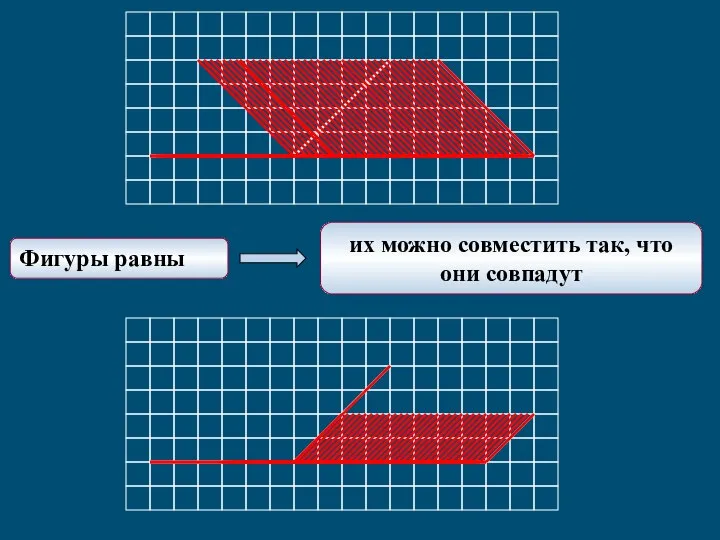 Равенство углов наложением
Равенство углов наложением Описательная статистика
Описательная статистика Применение производной к исследованию функции и построению графика
Применение производной к исследованию функции и построению графика mnozhestva_i_operatsii_nad_nimi (2)
mnozhestva_i_operatsii_nad_nimi (2) Решение заданий
Решение заданий Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение графика производной методом касательных
Построение графика производной методом касательных Ключевые задачи по теме пирамида
Ключевые задачи по теме пирамида Понятие множество и способы задания. 2 класс
Понятие множество и способы задания. 2 класс Древнеяпонские числительные. Задачи
Древнеяпонские числительные. Задачи Правильные многогранники
Правильные многогранники Можно ли без шаблона разметить круг?
Можно ли без шаблона разметить круг? Число потоков в графе
Число потоков в графе Логарифмы
Логарифмы Как не забыть математику за лето советы методиста
Как не забыть математику за лето советы методиста Отношение. Пропорция
Отношение. Пропорция Вероятность и статистика
Вероятность и статистика formuly_privedenia
formuly_privedenia Квадратные уравнения
Квадратные уравнения Сочетания. 9 класс
Сочетания. 9 класс Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Функциональная грамотность школьников на уроках математики
Функциональная грамотность школьников на уроках математики Движение
Движение Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г
Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников