Содержание
- 2. 2. Определители
- 3. Вильгельм Готфрид Лейбниц (1646-1716) — саксонский философ(1646-1716) — саксонский философ, логик(1646-1716) — саксонский философ, логик, математик,
- 4. Обозначения определителя матрицы А: |A|, det A, Δ. Определитель (детерминант) – числовая характеристика квадратной матрицы.
- 5. Невырожденная матрица Квадратная матрица А называется невырожденной, если её определитель det А≠0. В противном случае (det
- 6. Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем, следующим образом: 1.
- 7. 3. n = 3. Для вычислении определителя 3-го порядка используют правило треугольников (Саррюса).
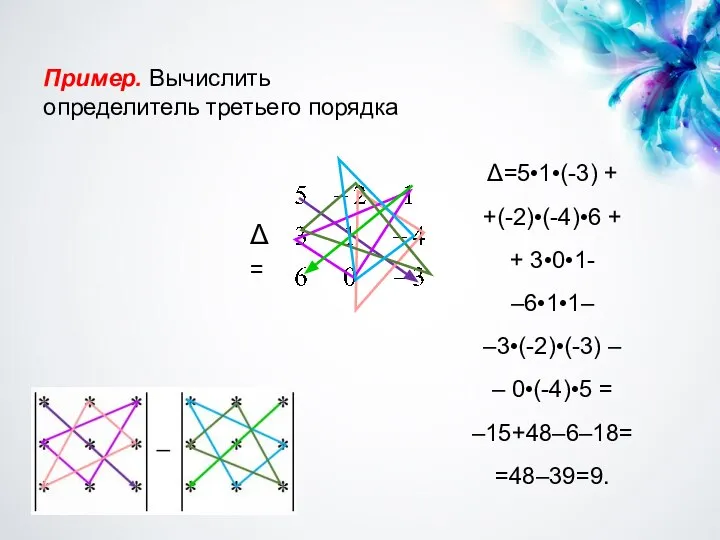
- 9. Пример. Вычислить определитель третьего порядка Δ=5•1•(-3) + +(-2)•(-4)•6 + + 3•0•1- –6•1•1– –3•(-2)•(-3) – – 0•(-4)•5
- 10. Пример. Вычислить определитель с помощью правила диагоналей - - - + + + Δ=5•1•(-3) + +(-2)•(-4)•6
- 11. Определитель произвольной треугольной матрицы равен произведению элементов главной диагонали
- 12. Минор элемента аi j Минором некоторого элемента aij квадратной матрицы А n-го порядка называется определитель n
- 13. Алгебраическое дополнение Aik Алгебраическим дополнением элемента aik квадратной матрицы А называется число Аik : Для предыдущего
- 14. ФОРМУЛА ЛАПЛАСА Теорема. Определитель матрицы равен сумме произведений элементов любого ее ряда на соответствующие им алгебраические
- 16. ПРАВИЛО ЧУЖИХ ДОПОЛНЕНИЙ Сумма произведений элементов любого ряда кв. матрицы на алгебраические дополнения соответствующих элементов другого
- 17. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ 1. Транспонирование матрицы не меняет значения ее определителя.
- 18. Свойства определителей 2. При перестановке двух параллельных рядов определитель меняет знак. 3. Если соответствующие элементы двух
- 19. 9. Если элементы какой-либо ряда квадратной матрицы А состоят из двух слагаемых, то определитель А равен
- 21. Скачать презентацию






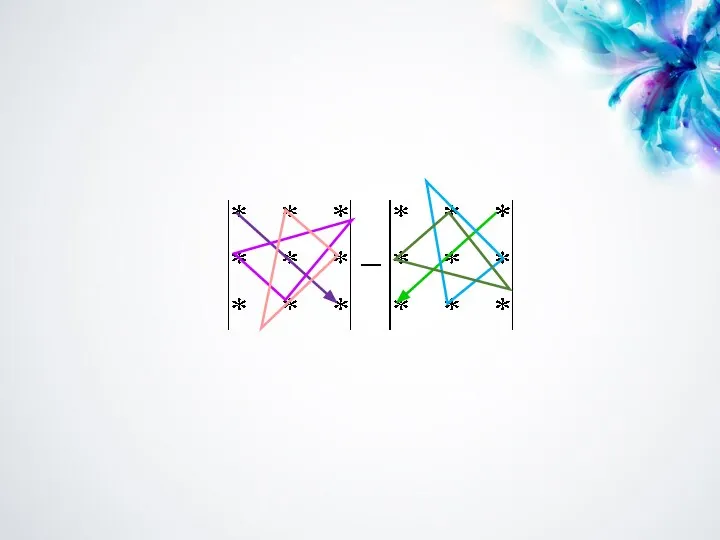





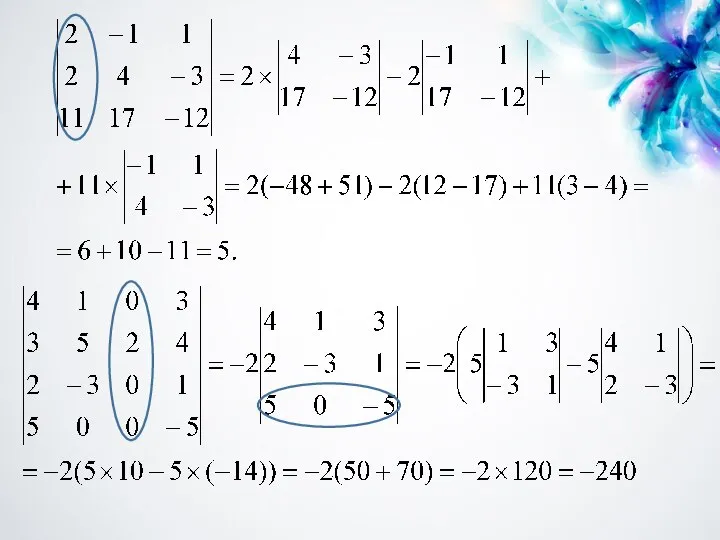




 Морской бой
Морской бой Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Таблица умножения
Таблица умножения Pervoobraznaya
Pervoobraznaya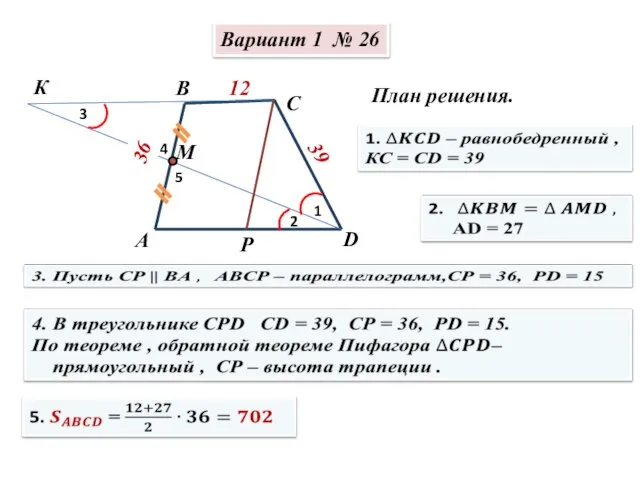 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Парадокс раздела ставки
Парадокс раздела ставки Теорема Пифагора
Теорема Пифагора Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями
Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Компетентность
Компетентность Логические задачи. 1 класс
Логические задачи. 1 класс Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Теорема Фалеса
Теорема Фалеса Умники и умницы. Викторина по математике
Умники и умницы. Викторина по математике Занимательные задачи
Занимательные задачи Лингвистика в математике
Лингвистика в математике Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Второй признак подобия треугольников
Второй признак подобия треугольников Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 L_3_U
L_3_U Повторение курса 5 класса
Повторение курса 5 класса Задачи с дробями
Задачи с дробями Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Решение задач с помощью геометрии
Решение задач с помощью геометрии