Содержание
- 2. Порядок роста и убывания функции Функция – это основной математический инструмент для изучения связей, зависимостей между
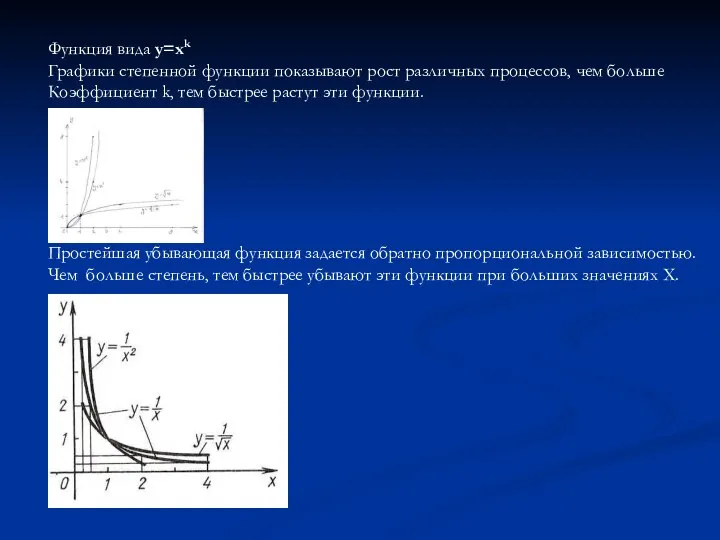
- 3. Функция вида y=xk Графики степенной функции показывают рост различных процессов, чем больше Коэффициент k, тем быстрее
- 4. В естествознании и технике встречаются процессы, рост или затухание которых происходят быстрее, чем у любой степенной
- 5. Показательные функции обладают замечательными свойствами: скорость их роста пропорциональна значению самой функции. Они как костёр, который,
- 6. Показательная функция Исследование показательных уравнений Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают
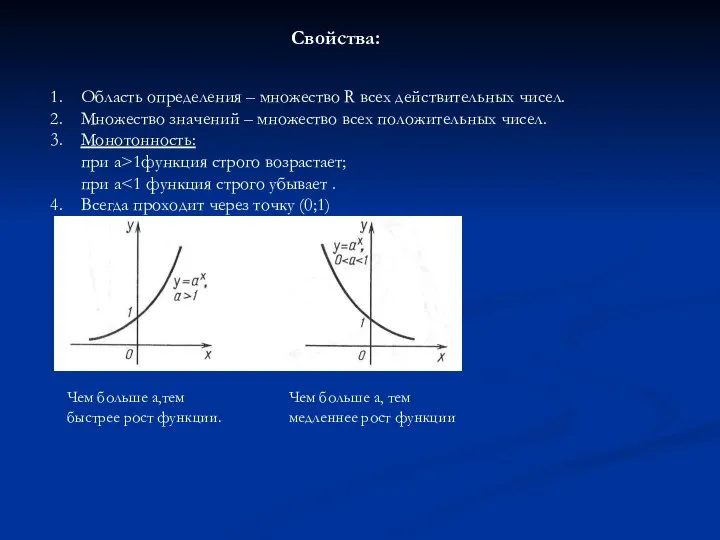
- 7. Свойства: Область определения – множество R всех действительных чисел. Множество значений – множество всех положительных чисел.
- 8. Число ℮ ℮ - иррациональное, трансцендентное число (не алгебраическое) Число ℮ можно представить как сумму: ℮=1+1/1+1/1∙
- 9. Джон Непер (16-17 вв.) Шотландский математик, изобретатель логарифмов. Учился в Эденбургском университете. В построении «Удивительной таблицы
- 11. Скачать презентацию






 Арифметические операции над матрицами
Арифметические операции над матрицами Формулы сокращённого умножения
Формулы сокращённого умножения Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Биномиальное распределение
Биномиальное распределение Треугольники
Треугольники Раздели на две части разными способами
Раздели на две части разными способами Построение равнобедренного треугольника
Построение равнобедренного треугольника Коллекция игр. 1 класс
Коллекция игр. 1 класс Презентация на тему Виды движения
Презентация на тему Виды движения  Математика. 2 класс. Задачи
Математика. 2 класс. Задачи Одночлен. 7 класс
Одночлен. 7 класс Линейные пространства и линейные операторы. Лекция 4
Линейные пространства и линейные операторы. Лекция 4 Математика. 1 класс
Математика. 1 класс Теорема косинусов
Теорема косинусов Проектирование точки на плоскости
Проектирование точки на плоскости Вопросы собеседования по математике для лиц, поступающих на базе среднего профессионального образования
Вопросы собеседования по математике для лиц, поступающих на базе среднего профессионального образования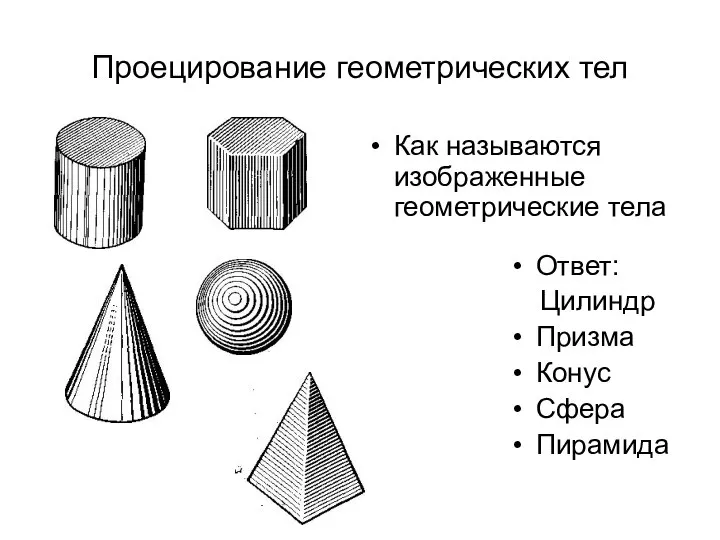 Построение геометрических тел
Построение геометрических тел График функции. Задания
График функции. Задания Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності
Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності Деление обыкновенных дробей
Деление обыкновенных дробей Межпредметные связи в реализации естественно-математического цикла в средней школе
Межпредметные связи в реализации естественно-математического цикла в средней школе Системы массового обслуживания с отказом
Системы массового обслуживания с отказом Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Площадь фигур. Единицы площади
Площадь фигур. Единицы площади Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей matematika_6_kl_04_10
matematika_6_kl_04_10 Центральная симметрия
Центральная симметрия Декартова прямоугольная система координат на плоскости
Декартова прямоугольная система координат на плоскости