Содержание
- 2. Цель: Изучить функцию y = cos x Задачи: 1. Изучить свойства функции у = cos x.
- 3. Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок
- 4. Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π] В координатной плоскости На числовой окружности
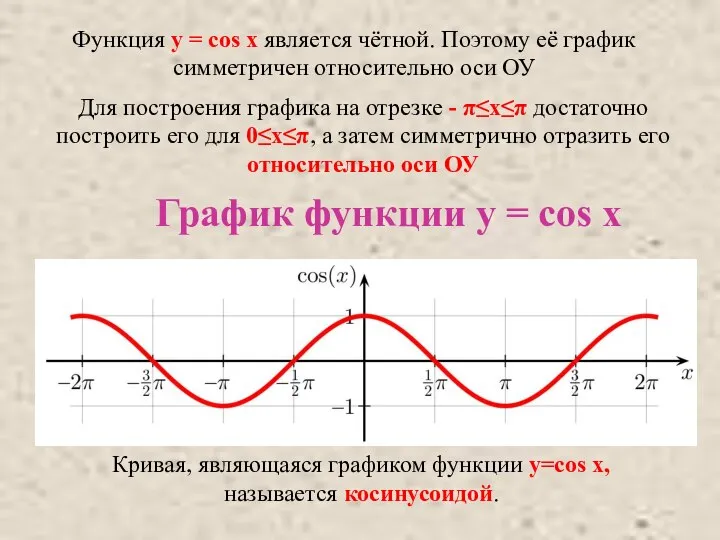
- 5. Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ Для построения
- 6. Свойства функции y = cos x 1. Область определения — множество R всех действительных чисел. D(y)
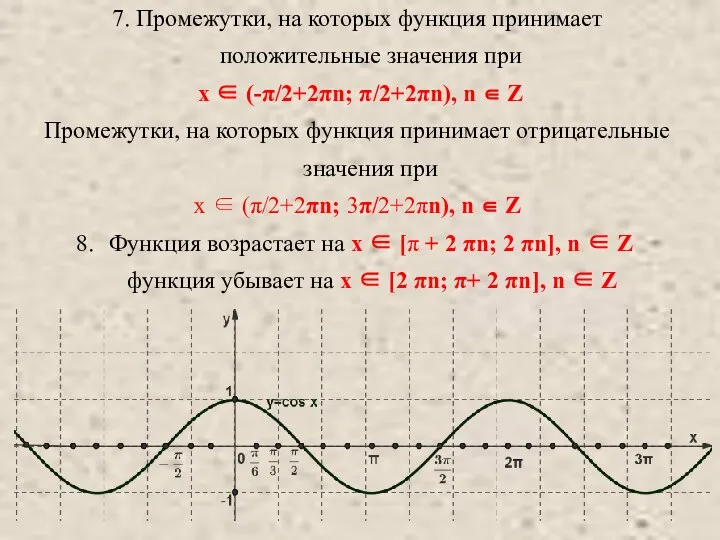
- 7. 7. Промежутки, на которых функция принимает положительные значения при x ∈ (-π/2+2πn; π/2+2πn), n ∈ Z
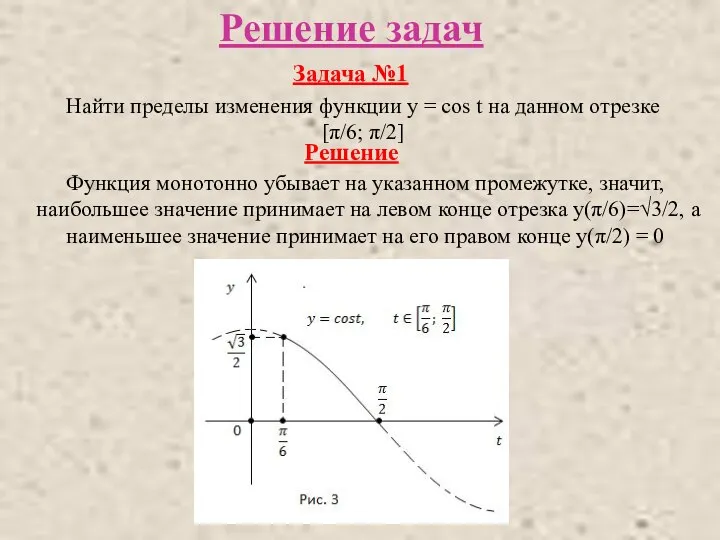
- 8. Решение задач Задача №1 Найти пределы изменения функции y = cos t на данном отрезке [π/6;
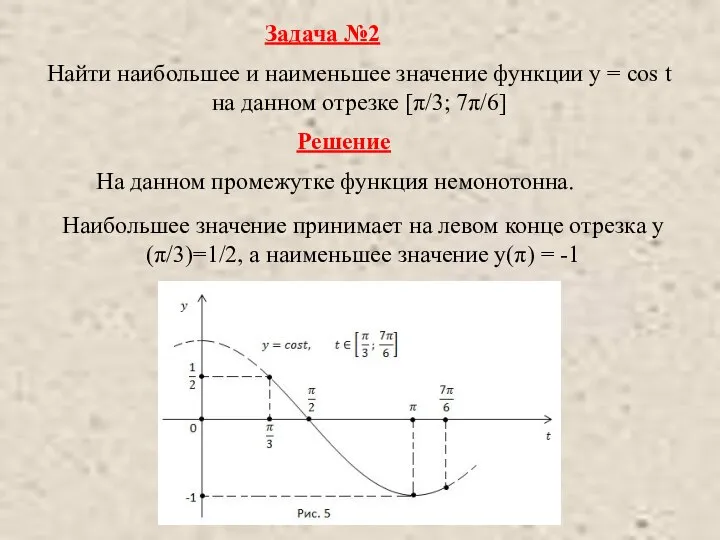
- 9. Задача №2 Найти наибольшее и наименьшее значение функции y = cos t на данном отрезке [π/3;
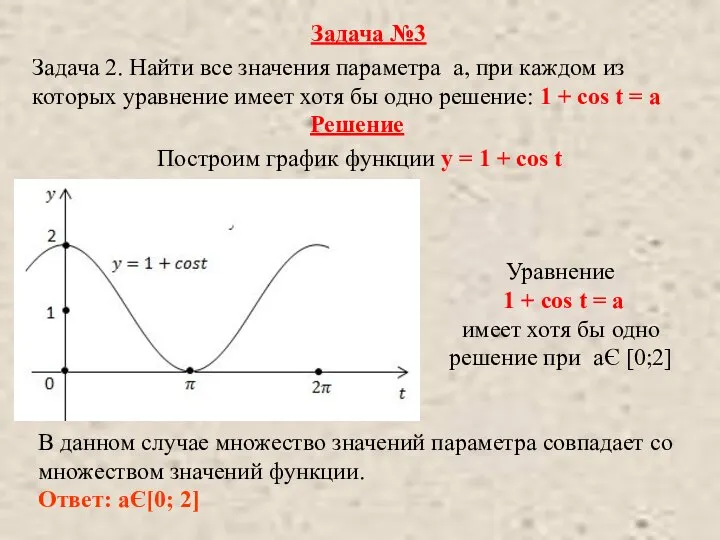
- 10. Задача 2. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы одно
- 11. Задача №4 Решить уравнение Построим в одних координатных осях графики функций Решение Графики имеют только одну
- 12. Задача №5 Найти число корней уравнения Решение На промежутке [-π; 0] функция у=cosx монотонно возрастает, функция
- 13. Построить график функции y=cos3x Задача №5 Косинус – четная функция, строим график на участке [0; π/3],
- 14. Задания для самостоятельного решения 1) Постройте графики функций 1) у = cosx + 1; 2) у
- 15. 3) Определить область значений функции y=−8cosx+3. 4) Определить чётность или нечётность функции: f(x)=x5⋅cos6x. 5) Определить, возрастает
- 17. Скачать презентацию


![Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π] В координатной плоскости На числовой окружности](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1164140/slide-3.jpg)


![Задача №5 Найти число корней уравнения Решение На промежутке [-π; 0] функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1164140/slide-11.jpg)



 Произведение многочленов
Произведение многочленов Презентация на тему Небесная геометрия - снежинки
Презентация на тему Небесная геометрия - снежинки  Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств презентация к уроку по теме_ _Трапеция_ (8 класс, Атанасян)
презентация к уроку по теме_ _Трапеция_ (8 класс, Атанасян) Деление на натуральное число и деление на десятичную дробь
Деление на натуральное число и деление на десятичную дробь Деление десятичных дробей
Деление десятичных дробей Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год Комбинаторика. Курс лекций Дискретная математика
Комбинаторика. Курс лекций Дискретная математика Комбинаторика
Комбинаторика Карточки-задания по теме Конус. Содержат алгоритм решения
Карточки-задания по теме Конус. Содержат алгоритм решения Приближенные вычисления
Приближенные вычисления Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Презентация на тему Упрощение выражений (6 класс)
Презентация на тему Упрощение выражений (6 класс)  Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Семейство четырехугольников
Семейство четырехугольников ЛЕКЦИЯ_7
ЛЕКЦИЯ_7 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Деление дробей
Деление дробей Векторы в пространстве
Векторы в пространстве Умножение и деление десятичной дроби на 10, 100, 1000
Умножение и деление десятичной дроби на 10, 100, 1000 Подготовка к ВПР (8 класс)
Подготовка к ВПР (8 класс)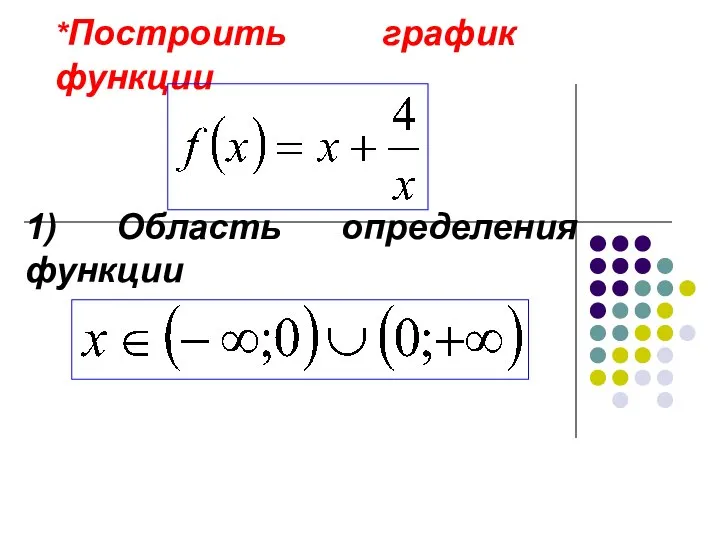 Построение графиков функций
Построение графиков функций Презентация на тему Деление десятичных дробей
Презентация на тему Деление десятичных дробей  Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Призма. Площадь полной поверхности прямой призмы
Призма. Площадь полной поверхности прямой призмы Дифференциальные уравнения
Дифференциальные уравнения