Задания ЕГЭ

1-1
Для каж­до­го из пе­ре­чис­лен­ных ниже чисел по­стро­и­ли дво­ич­ную за­пись. Ука­жи­те число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит ровно два зна­ча­щих нуля. Если таких чисел не­сколь­ко, ука­жи­те наи­боль­шее из них.
7
8
9
10

1-2
Ука­жи­те наи­мень­шее четырёхзнач­ное шест­на­дца­те­рич­ное число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит ровно 5 нулей. В от­ве­те за­пи­ши­те толь­ко само шест­на­дца­те­рич­ное число, ос­но­ва­ние си­сте­мы счис­ле­ния ука­зы­вать не нужно.

1-3
Ука­жи­те наи­мень­шее четырёхзнач­ное вось­ме­рич­ное число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит 5 еди­ниц. В от­ве­те за­пи­ши­те толь­ко само вось­ме­рич­ное число, ос­но­ва­ние си­сте­мы счис­ле­ния ука­зы­вать не нужно.

1-4
Ука­жи­те наи­мень­шее четырёхзнач­ное вось­ме­рич­ное число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит ровно 4 нуля. В от­ве­те за­пи­ши­те толь­ко само вось­ме­рич­ное число, ос­но­ва­ние си­сте­мы счис­ле­ния ука­зы­вать не нужно.

1-5

1-6

1-7

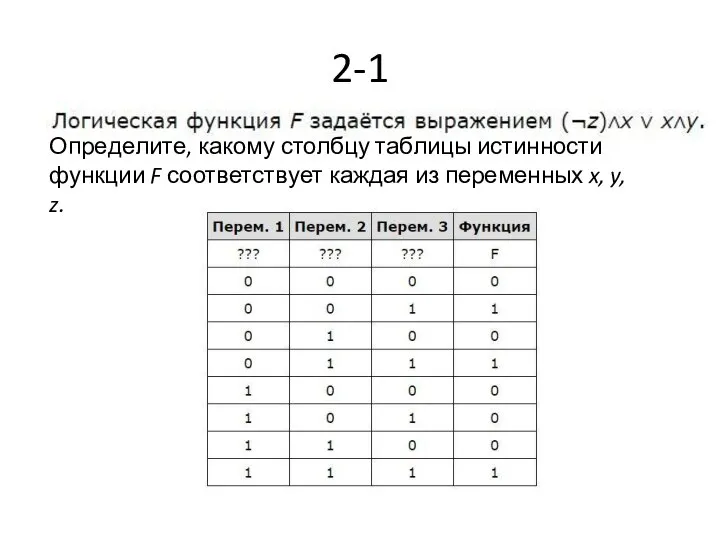
2-1
Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­дая из пе­ре­мен­ных x, y, z.

Ответ: zyx

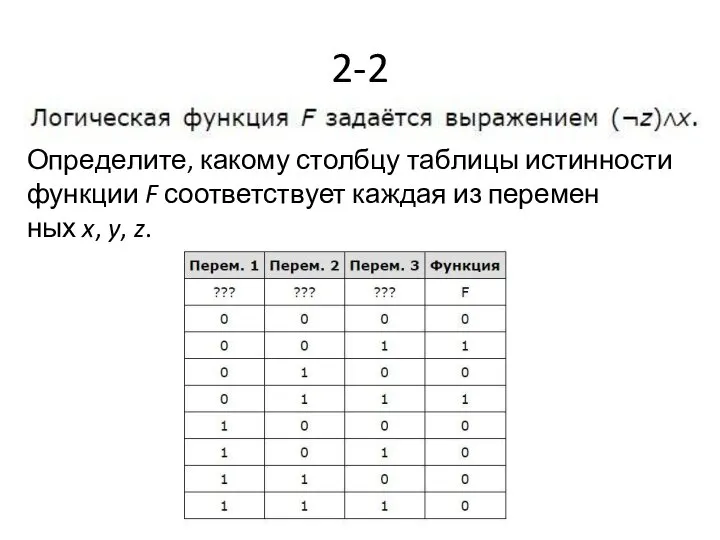
2-2
Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­дая из пе­ре­мен­ных x, y, z.

Ответ: zyx.

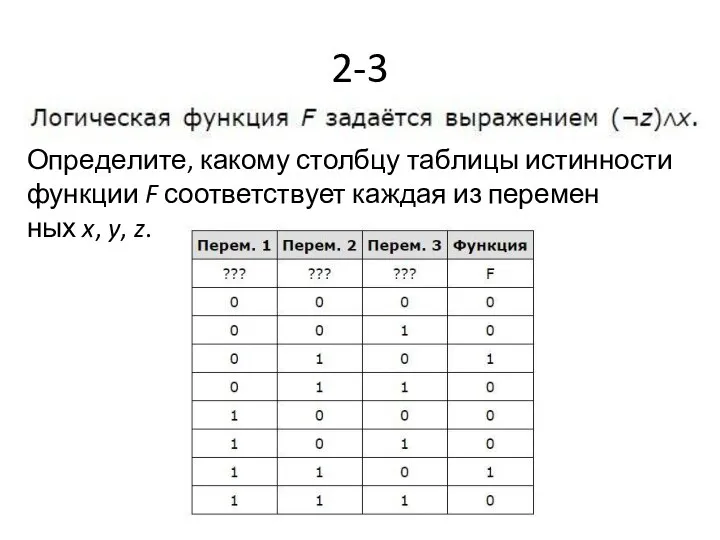
2-3
Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­дая из пе­ре­мен­ных x, y, z.

Ответ: yxz.

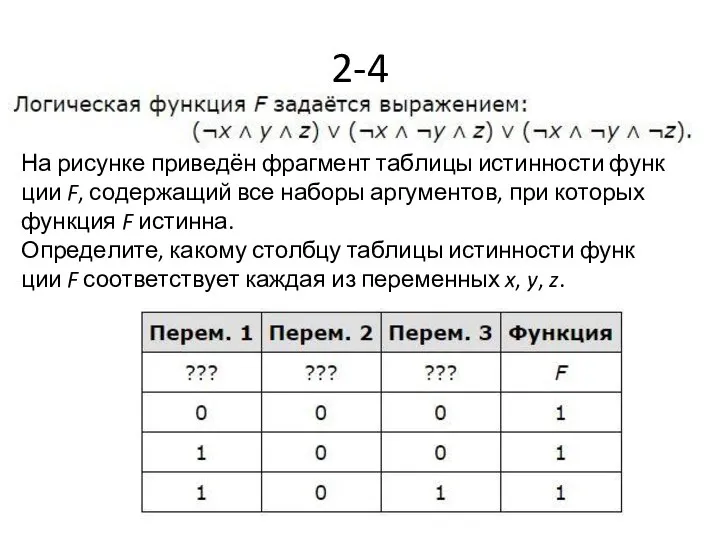
2-4
На ри­сун­ке при­ведён фраг­мент таб­ли­цы ис­тин­но­сти функ­ции F, со­дер­жа­щий все на­бо­ры ар­гу­мен­тов, при ко­то­рых функ­ция F ис­тин­на.
Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­дая из пе­ре­мен­ных x, y, z.

Ответ: zxy.

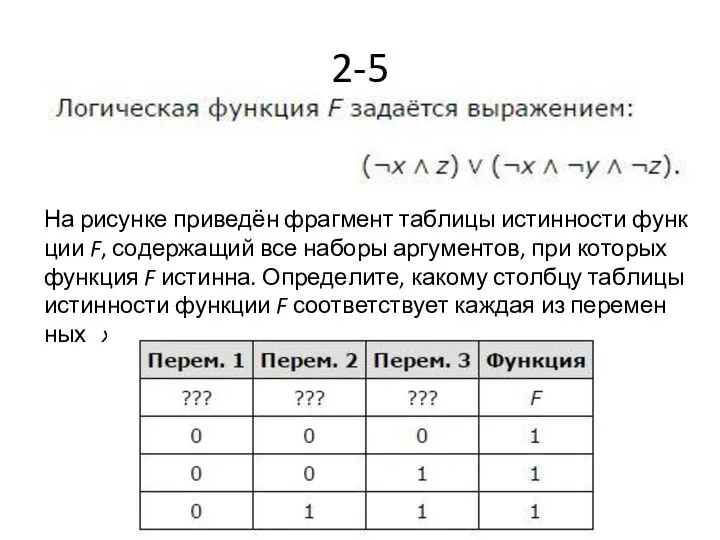
2-5
На ри­сун­ке при­ведён фраг­мент таб­ли­цы ис­тин­но­сти функ­ции F, со­дер­жа­щий все на­бо­ры ар­гу­мен­тов, при ко­то­рых функ­ция F ис­тин­на. Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­дая из пе­ре­мен­ных x, y, z.

Ответ: xyz.

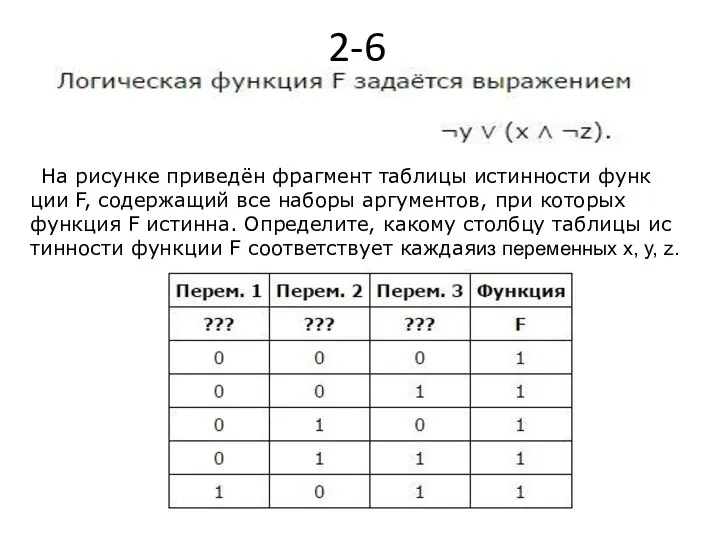
2-6
На ри­сун­ке при­ведён фраг­мент таб­ли­цы ис­тин­но­сти функ­ции F, со­дер­жа­щий все на­бо­ры ар­гу­мен­тов, при ко­то­рых функ­ция F ис­тин­на. Опре­де­ли­те, ка­ко­му столб­цу таб­ли­цы ис­тин­но­сти функ­ции F со­от­вет­ству­ет каж­даяиз пе­ре­мен­ных x, y, z.

Ответ: yzx.

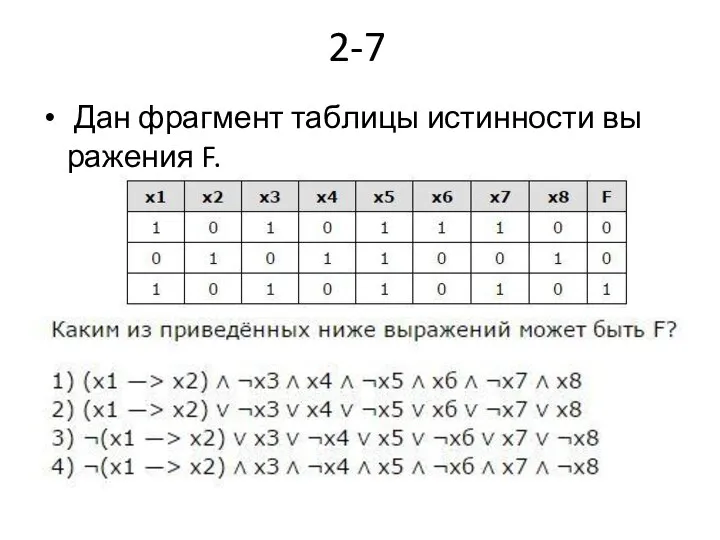
2-7
Дан фраг­мент таб­ли­цы ис­тин­но­сти вы­ра­же­ния F.

Правильный ответ — 4.

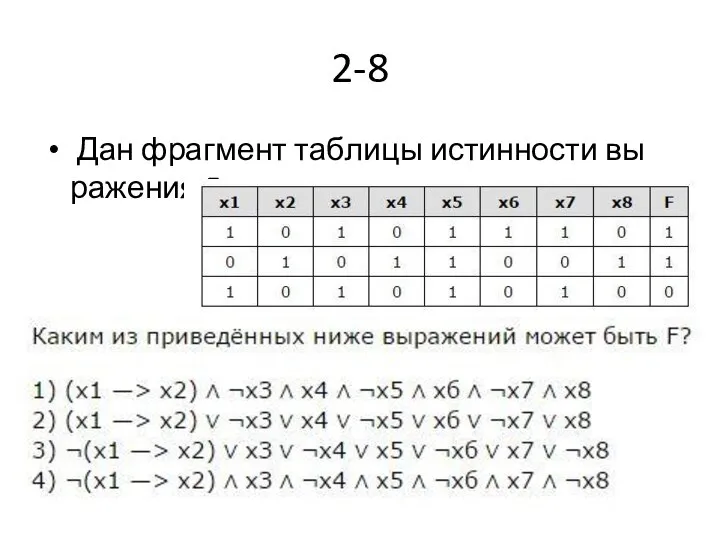
2-8
Дан фраг­мент таб­ли­цы ис­тин­но­сти вы­ра­же­ния F.

Правильный ответ — 2.

2-9
Сим­во­лом F обо­зна­че­но одно из ука­зан­ных ниже ло­ги­че­ских вы­ра­же­ний от трех ар­гу­мен­тов: X, Y, Z. Дан фраг­мент таб­ли­цы ис­тин­но­сти вы­ра­же­ния F:

вариант 2 является ответом к данной задаче.

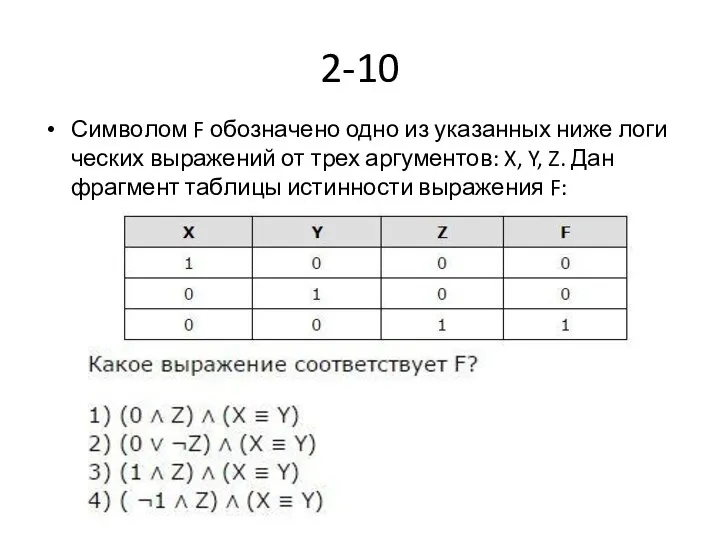
2-10
Сим­во­лом F обо­зна­че­но одно из ука­зан­ных ниже ло­ги­че­ских вы­ра­же­ний от трех ар­гу­мен­тов: X, Y, Z. Дан фраг­мент таб­ли­цы ис­тин­но­сти вы­ра­же­ния F:

вариант 3 является ответом к данной задаче .

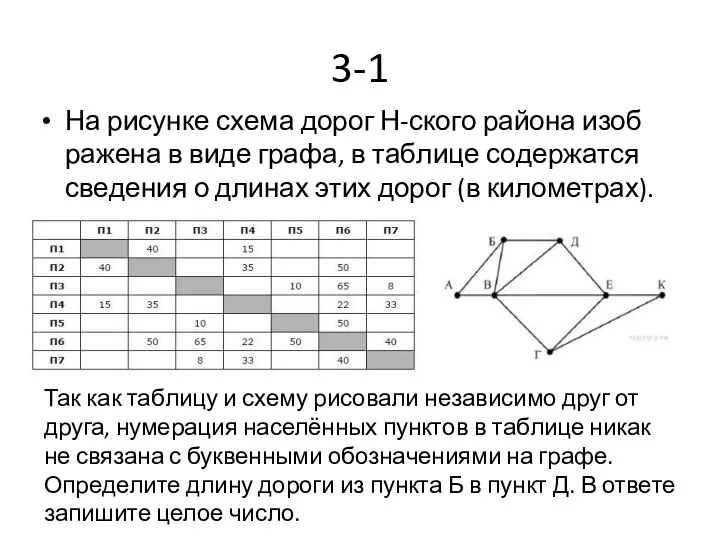
3-1
На ри­сун­ке схема дорог Н-ского рай­о­на изоб­ра­же­на в виде графа, в таб­ли­це со­дер­жат­ся све­де­ния о дли­нах этих дорог (в ки­ло­мет­рах).
Так как таб­ли­цу и схему ри­со­ва­ли не­за­ви­си­мо друг от друга, ну­ме­ра­ция населённых пунк­тов в таб­ли­це никак не свя­за­на с бук­вен­ны­ми обо­зна­че­ни­я­ми на графе. Опре­де­ли­те длину до­ро­ги из пунк­та Б в пункт Д. В от­ве­те за­пи­ши­те целое число.

3-1 Решение
Есть толь­ко один пункт, из ко­то­ро­го ведёт 5 дорог - это В, а в таб­ли­це - П6.
Из А ведёт две до­ро­ги и одна из них в В. В таб­ли­це та­ко­му со­от­вет­ству­ет П5.
Из Б ведёт 3 до­ро­ги, причём есть до­ро­ги в А и в В, в таб­ли­це под такое под­хо­дит толь­ко П3.
Из Д три до­ро­ги, две из ко­то­рых в Б и в В, в таб­ли­це толь­ко один пункт та­ко­му со­от­вет­ству­ет - П7.
Таким об­ра­зом, Б - это П3, а Д - П7. Длина до­ро­ги между П3 и П7 - 8.

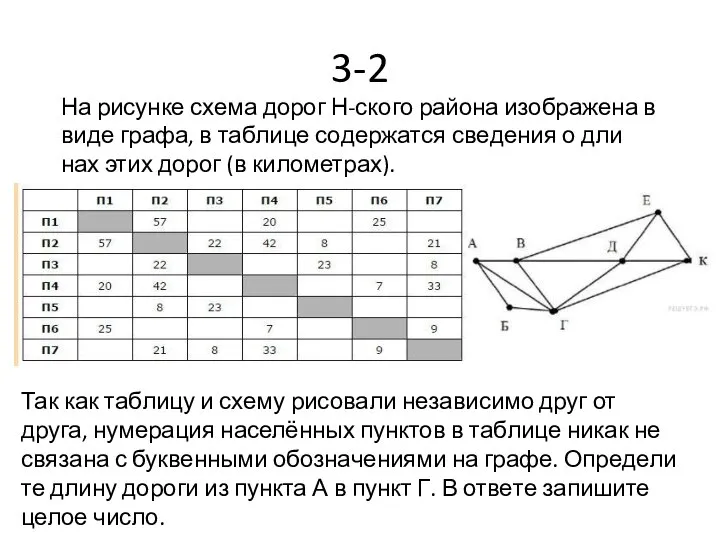
3-2
На ри­сун­ке схема дорог Н-ского рай­о­на изоб­ра­же­на в виде графа, в таб­ли­це со­дер­жат­ся све­де­ния о дли­нах этих дорог (в ки­ло­мет­рах).
Так как таб­ли­цу и схему ри­со­ва­ли не­за­ви­си­мо друг от друга, ну­ме­ра­ция населённых пунк­тов в таб­ли­це никак не свя­за­на с бук­вен­ны­ми обо­зна­че­ни­я­ми на графе. Опре­де­ли­те длину до­ро­ги из пунк­та А в пункт Г. В от­ве­те за­пи­ши­те целое число.

3-2 решение
На карте есть толь­ко один пункт с 5 до­ро­га­ми, это Г. В таб­ли­це же это П2.
На карте есть толь­ко один пункт с 2 до­ро­га­ми, это Б. В таб­ли­це же это П5.
А - пункт, из ко­то­ро­го вы­хо­дит 3 до­ро­ги, ко­то­рый свя­зан и с Г, и с Б. Из всех пунк­тов в таб­ли­це толь­ко П3 под это под­хо­дит.
Таким об­ра­зом, Г = П2, А = П3. Длина до­ро­ги между П2 и П3 - 22.

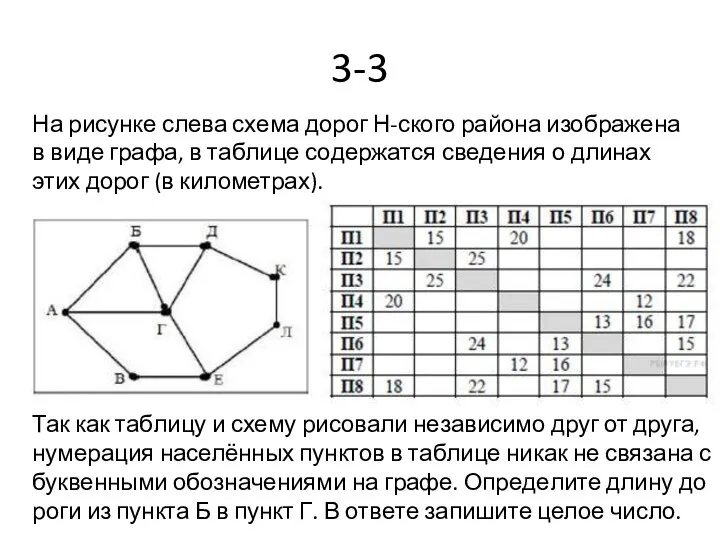
3-3
На ри­сун­ке слева схема дорог Н-ского рай­о­на изоб­ра­же­на в виде графа, в таб­ли­це со­дер­жат­ся све­де­ния о дли­нах этих дорог (в ки­ло­мет­рах).
Так как таб­ли­цу и схему ри­со­ва­ли не­за­ви­си­мо друг от друга, ну­ме­ра­ция населённых пунк­тов в таб­ли­це никак не свя­за­на с бук­вен­ны­ми обо­зна­че­ни­я­ми на графе. Опре­де­ли­те длину до­ро­ги из пунк­та Б в пункт Г. В от­ве­те за­пи­ши­те целое число.

3-3 решение
Со­по­ста­вим населённые пунк­ты графа и населённые пунк­ты в таб­ли­це.
Из Б ведут три до­ро­ги. Из пунк­тов П1, П3, П5, П6 также ведут три до­ро­ги. За­ме­тим, что из Б до­ро­ги идут в пунк­ты с тремя, че­тырь­мя и тремя до­ро­га­ми. Со­по­став­ляя с таб­ли­цей, по­лу­чим, что Б со­от­вет­ству­ет пунк­ту П6.
Из Г ведут че­ты­ре до­ро­ги. Толь­ко из пунк­та П8 ведут че­ты­ре до­ро­ги, сле­до­ва­тель­но, пункт П8 — это и есть Г.
Длина до­ро­ги из П6 в П8 равна 15.
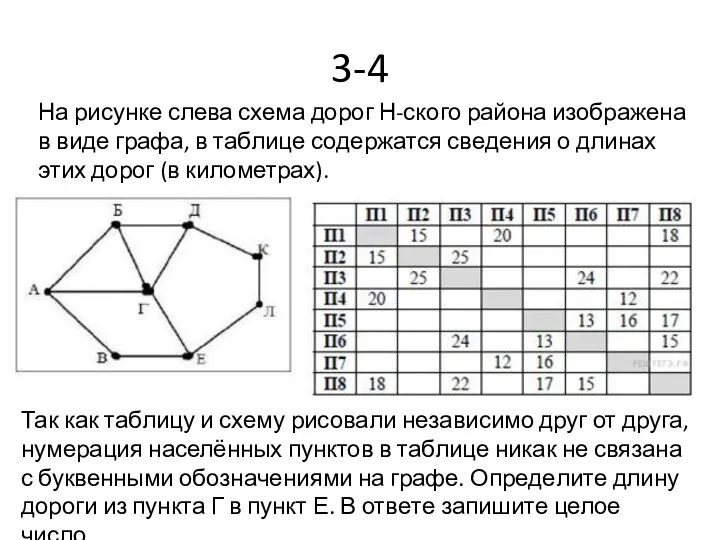
Ответ: 15.

3-4
На ри­сун­ке слева схема дорог Н-ского рай­о­на изоб­ра­же­на в виде графа, в таб­ли­це со­дер­жат­ся све­де­ния о дли­нах этих дорог (в ки­ло­мет­рах).
Так как таб­ли­цу и схему ри­со­ва­ли не­за­ви­си­мо друг от друга, ну­ме­ра­ция населённых пунк­тов в таб­ли­це никак не свя­за­на с бук­вен­ны­ми обо­зна­че­ни­я­ми на графе. Опре­де­ли­те длину до­ро­ги из пунк­та Г в пункт Е. В от­ве­те за­пи­ши­те целое число.

Сопоставим населённые пунк­ты графа и населённые пунк­ты в таблице.
Из Г ведут че­ты­ре дороги. Толь­ко из пунк­та П8 ведут че­ты­ре дороги, следовательно, пункт П8 — это и есть Г.
Из Е ведут три дороги. Из пунк­тов П1, П3, П5, П6 также ведут три дороги. Заметим, что из Е до­ро­ги идут в пунк­ты с двумя, че­тырь­мя и двумя дорогами. Со­по­став­ляя с таблицей, получим, что Е со­от­вет­ству­ет пунк­ту П1.
Длина до­ро­ги из П1 в П8 равна 18.
Ответ: 18.

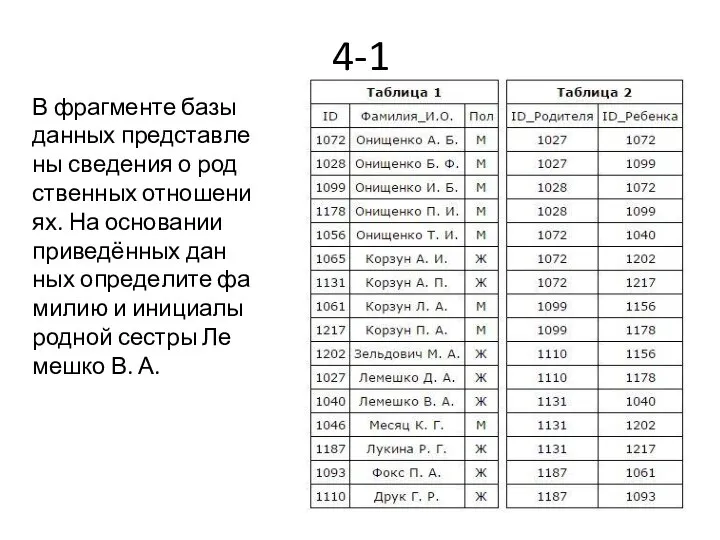
4-1
В фраг­мен­те базы дан­ных пред­став­ле­ны све­де­ния о род­ствен­ных от­но­ше­ни­ях. На ос­но­ва­нии при­ведённых дан­ных опре­де­ли­те фа­ми­лию и ини­ци­а­лы род­ной сест­ры Ле­меш­ко В. А.

1) ID Ле­меш­ко В. А.: 1040.
2) Из таб­ли­цы 2 определяем, что ID ро­ди­те­лей Ле­меш­ко В. А.: 1072, 1131.
3) Из таб­ли­цы 2 определяем, что ID бра­тьев и се­стер Ле­меш­ко В. А.: 1202, 1217.
4) Из таб­ли­цы 1 определяем, что сест­ра Ле­меш­ко В. А. — Зель­до­вич М. А.
Ответ: 1202.

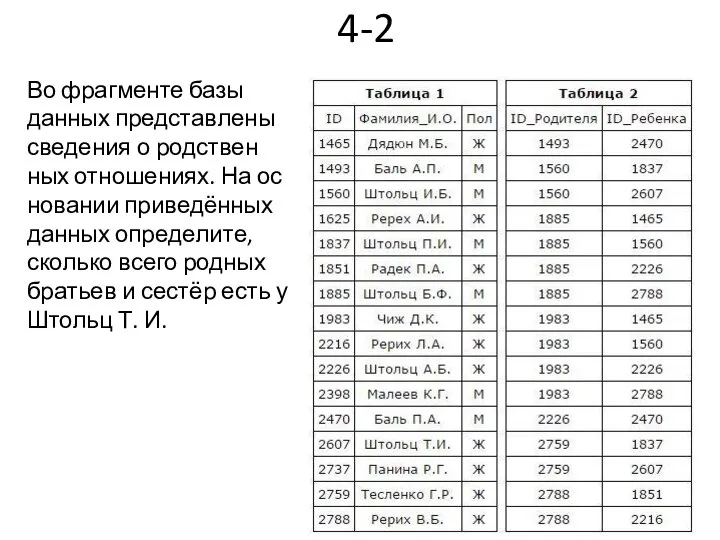
4-2
Во фраг­мен­те базы дан­ных пред­став­ле­ны све­де­ния о род­ствен­ных от­но­ше­ни­ях. На ос­но­ва­нии при­ведённых дан­ных опре­де­ли­те, сколь­ко всего род­ных бра­тьев и сестёр есть у Штольц Т. И.

По первой таблице видно, что ID Штольц Т. И. равен 2607. Найдем во второй таблице в графе «ID_ребенка» номер Штольц Т. И. Видно, что его родители имеют ID 2759 и 1560. Теперь найдем в графе «ID_ребенка» братьев и сестер Штольц Т. И. Это человек с ID 1837.

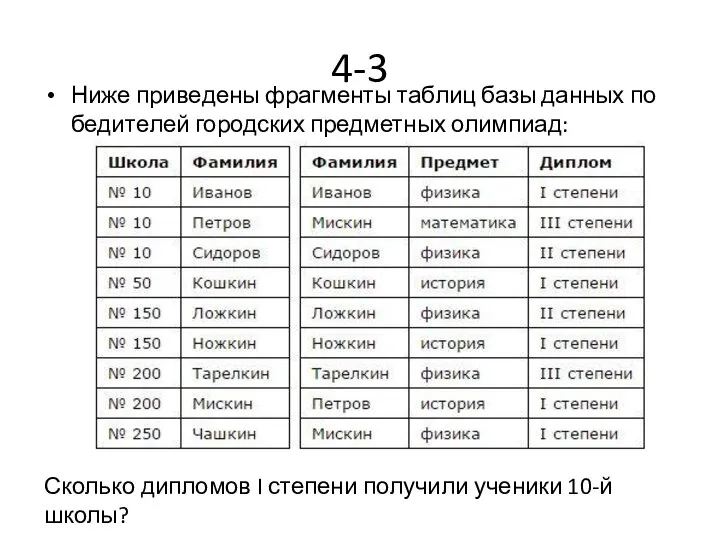
4-3
Ниже при­ве­де­ны фраг­мен­ты таб­лиц базы дан­ных по­бе­ди­те­лей го­род­ских пред­мет­ных олим­пи­ад:
Сколь­ко ди­пло­мов I сте­пе­ни по­лу­чи­ли уче­ни­ки 10-й школы?

3. Ди­пло­мы первой сте­пе­ни получили толь­ко Иванов и Петров, т.е. два ученика.

5-1
Для ко­ди­ро­ва­ния букв И, Д, Т, О, X ре­ши­ли ис­поль­зо­вать дво­ич­ное пред­став­ле­ние чисел 0, 1, 2, 3 и 4 со­от­вет­ствен­но (с со­хра­не­ни­ем од­но­го не­зна­ча­ще­го нуля в слу­чае од­но­раз­ряд­но­го пред­став­ле­ния). Если за­ко­ди­ро­вать по­сле­до­ва­тель­ность букв ТИ­ХО­ХОД таким спо­со­бом и ре­зуль­тат за­пи­сать шест­на­дца­те­рич­ным кодом, то по­лу­чит­ся

1000 1001 1100 1101 — 8 9 12 13 — 89СD.

5-2
Для ко­ди­ро­ва­ния букв Р, С, Н, О, Г ре­ши­ли ис­поль­зо­вать дво­ич­ное пред­став­ле­ние чисел 0, 1, 2, 3 и 4 со­от­вет­ствен­но (с со­хра­не­ни­ем од­но­го не­зна­ча­ще­го нуля в слу­чае од­но­раз­ряд­но­го пред­став­ле­ния). Если за­ко­ди­ро­вать по­сле­до­ва­тель­ность букв НО­СО­РОГ таким спо­со­бом и ре­зуль­тат за­пи­сать вось­ме­рич­ным кодом, то по­лу­чит­ся

101 101 110 011 100 — 55634.

5-3
Для 6 букв ла­тин­ско­го ал­фа­ви­та за­да­ны их дво­ич­ные коды (для не­ко­то­рых букв из двух бит, для не­ко­то­рых – из трех). Эти коды пред­став­ле­ны в таб­ли­це:
Опре­де­ли­те, какая по­сле­до­ва­тель­ность из 6 букв за­ко­ди­ро­ва­на дво­ич­ной стро­кой 011111000101100.

Окончательно получили ответ: DECAFB.

5-4
Для ко­ди­ро­ва­ния не­ко­то­рой по­сле­до­ва­тель­но­сти, со­сто­я­щей из букв И, К, Л, М, Н, ре­ши­ли ис­поль­зо­вать не­рав­но­мер­ный дво­ич­ный код, удо­вле­тво­ря­ю­щий усло­вию Фано. Для буквы Л ис­поль­зо­ва­ли ко­до­вое слово 1, для буквы М – ко­до­вое слово 01. Ка­ко­ва наи­мень­шая воз­мож­ная сум­мар­ная длина всех пяти ко­до­вых слов?
При­ме­ча­ние. Усло­вие Фано озна­ча­ет, что ни­ка­кое ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го ко­до­во­го слова. Это обес­пе­чи­ва­ет воз­мож­ность од­но­знач­ной рас­шиф­ров­ки за­ко­ди­ро­ван­ных со­об­ще­ний.

5-4 решение
Усло­вие Фано — ни­ка­кое ко­до­вое слово не может быть на­ча­лом дру­го­го ко­до­во­го слова. Так как уже име­ет­ся ко­до­вое слово 1, то ни­ка­кое дру­гое не может на­чи­нать­ся с 1. Толь­ко с 0.
Также не может на­чи­нать­ся с 01, по­сколь­ку у нас уже есть 01. То есть любое новое ко­до­вое слово будет на­чи­нать­ся с 00. Но это не может быть 00, так как иначе мы не смо­жем взять боль­ше ни од­но­го ко­до­во­го слова, по­сколь­ку все более длин­ные слова на­чи­на­ют­ся либо с 1, либо с 00, либо с 01.
Мы можем взять либо 000, либо 001. Но не оба сразу, по­сколь­ку опять же в таком слу­чае мы боль­ше не смо­жем взять ни од­но­го но­во­го кода. Тогда возьмём 001. И так как нам оста­лось всего два кода, то можем взять 0000 и 0001. Итого имеем: 1, 01, 001, 0000, 0001. Всего 14 сим­во­лов.

5-5
Для ко­ди­ро­ва­ния не­ко­то­рой по­сле­до­ва­тель­но­сти, со­сто­я­щей из букв И, К, Л, М, Н, ре­ши­ли ис­поль­зо­вать не­рав­но­мер­ный дво­ич­ный код, удо­вле­тво­ря­ю­щий усло­вию Фано. Для буквы Н ис­поль­зо­ва­ли ко­до­вое слово 0, для буквы К – ко­до­вое слово 10. Ка­ко­ва наи­мень­шая воз­мож­ная сум­мар­ная длина всех пяти ко­до­вых слов?
При­ме­ча­ние. Усло­вие Фано озна­ча­ет, что ни­ка­кое ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го ко­до­во­го слова. Это обес­пе­чи­ва­ет воз­мож­ность од­но­знач­ной рас­шиф­ров­ки за­ко­ди­ро­ван­ных со­об­ще­ний.

5-6
По ка­на­лу связи пе­ре­да­ют­ся со­об­ще­ния, со­дер­жа­щие толь­ко шесть букв: А, B, C, D, E, F. Для пе­ре­да­чи ис­поль­зу­ет­ся не­рав­но­мер­ный дво­ич­ный код, удо­вле­тво­ря­ю­щий усло­вию Фано. Для букв A, B, C ис­поль­зу­ют­ся такие ко­до­вые слова: А – 00, B – 010, C – 1. Ка­ко­ва наи­мень­шая воз­мож­ная сум­мар­ная длина всех ко­до­вых слов?
При­ме­ча­ние. Усло­вие Фано озна­ча­ет, что ни одно ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го ко­до­во­го слова. Коды, удо­вле­тво­ря­ю­щие усло­вию Фано, до­пус­ка­ют од­но­знач­ное де­ко­ди­ро­ва­ние.

5-6 решение
За­ме­тим, что для ал­фа­ви­та из трёх букв, код с наи­мень­шей сум­мар­ной дли­ной ко­до­вых слов, удо­вле­тво­ря­ю­щий усло­вию Фано имел бы длину 1 + 2 + 2 = 5. Для ал­фа­ви­та из четырёх букв: 1 + 2 + 3 + 3 = 9. Ана­ло­гич­но можно по­лу­чить ми­ни­маль­ную длину сум­мар­ную длину ко­до­вых слов для ал­фа­ви­та, со­дер­жа­ще­го про­из­воль­ное число сим­во­лов.
Удо­сто­ве­рим­ся, что, ис­поль­зуя ко­до­вые слова, при­ведённые в усло­вии можно по­стро­ить код, удо­вле­тво­ря­ю­щий усло­вию Фано и име­ю­щий наи­мень­шую сум­мар­ную длину. Будем ис­поль­зо­вать для буквы D ко­до­вое слово 0110, для буквы E ко­до­вое слово 01110, для буквы F 01111.
Сум­мар­ная длина та­ко­го кода 1 + 2 + 3 + 4 + 5 + 5 = 20.
Ответ: 20.