- Главная
- Математика
- Случайные величины

Содержание
- 2. Непрерывные случайные величины. Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел,
- 3. Равномерное распределение функции распределения График функции . Заметим, что в точках a и b функция терпит
- 4. Нормальное распределение Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса, если ее плотность
- 6. Скачать презентацию
Слайд 2Непрерывные случайные величины.
Кроме дискретных случайных величин, возможные значения которых образуют конечную
Непрерывные случайные величины. Кроме дискретных случайных величин, возможные значения которых образуют конечную

или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х).
Эта функция определяется точно так же, как и в случае дискретной случайной величины:
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству
Эта функция определяется точно так же, как и в случае дискретной случайной величины:
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству
Слайд 3Равномерное распределение
функции распределения
График функции . Заметим, что в точках a и
Равномерное распределение
функции распределения
График функции . Заметим, что в точках a и
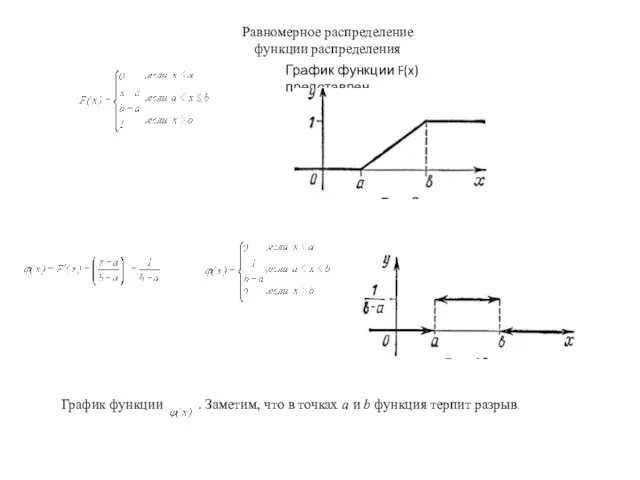
b функция терпит разрыв.
График функции F(x) представлен
Слайд 4Нормальное распределение
Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса,
Нормальное распределение
Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса,
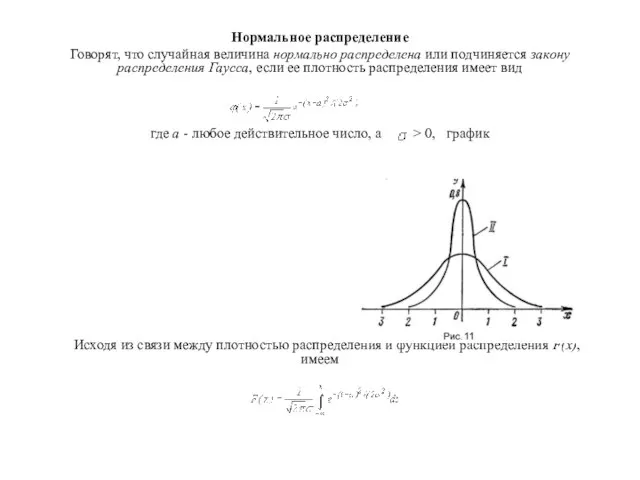
если ее плотность распределения имеет вид
где a - любое действительное число, а > 0, график
Исходя из связи между плотностью распределения и функцией распределения F(x), имеем
где a - любое действительное число, а > 0, график
Исходя из связи между плотностью распределения и функцией распределения F(x), имеем
Следующая -
День семьи. Выставка книг Признаки параллельности прямых
Признаки параллельности прямых Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Простейшие векторные операции и их реализация на языке MATLAB
Простейшие векторные операции и их реализация на языке MATLAB Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) График линейной функции
График линейной функции 20e
20e Координатная плоскость (урок 3)
Координатная плоскость (урок 3) Карточки по математике. Состав числа
Карточки по математике. Состав числа Векторы в пространстве
Векторы в пространстве Математический кроссворд
Математический кроссворд Бутылка Клейна
Бутылка Клейна Статистика. Занятие 4
Статистика. Занятие 4 Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ  Интервальное оценивание параметров распределения случайных величин. Доверительный интервал
Интервальное оценивание параметров распределения случайных величин. Доверительный интервал формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Гармония хаоса или хаотичная реальность
Гармония хаоса или хаотичная реальность Решение квадратных уравнений выделением квадрата двучлена
Решение квадратных уравнений выделением квадрата двучлена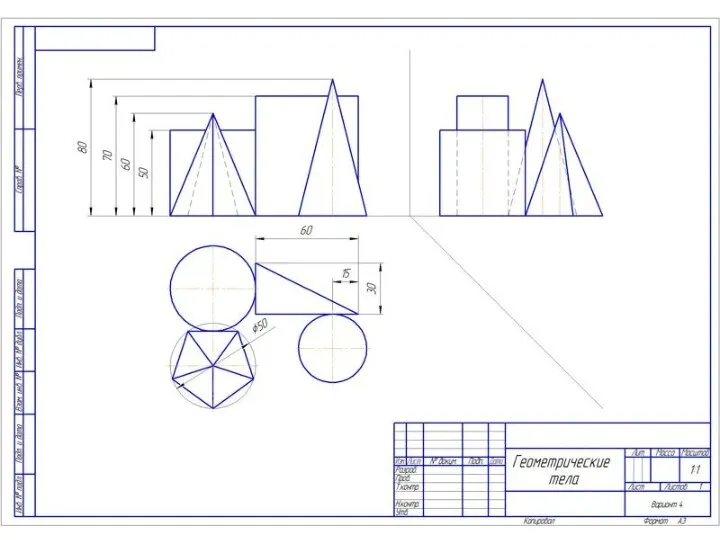 Геометрические тела. 9 класс
Геометрические тела. 9 класс Соединения с повторениями
Соединения с повторениями Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций Процент - это одна сотая часть
Процент - это одна сотая часть Определенный интеграл. Формула Ньютона - Лейбница
Определенный интеграл. Формула Ньютона - Лейбница Функции нескольких переменных. Предел и непрерывность
Функции нескольких переменных. Предел и непрерывность Параметрическая стандартизация. Ряды предпочтительных чисел
Параметрическая стандартизация. Ряды предпочтительных чисел