Многофакторный дисперсионный анализ. Многомерный дисперсионный анализ. Трактовка результатов. Линейные модели

Адекватное планирование исследовательской работы – явление редкое => проблема множественности сравнений как для 1 комбинации переменных для подгрупп, так и в целом по исследованию! Проблема взаимодействия факторов!
Р=0,05 – в одном случае из 20 различия будут значимыми СЛУЧАЙНО!!! => Если различий больше 1 – получаемое «сырое» значение р не является «истинным»!
Если независимых переменных больше 1 => статистический анализ сразу становится небанальной задачей! Две группы + стадия из 3 уровней – попарными сравнениями эту задачу УЖЕ НЕ РЕШИТЬ!
В литературе (даже высокого уровня) это учитывают редко (ДО СИХ ПОР!); + медицинские публикации подвержены «моде» на сложные методы, трактовка которых сложнее, а чувствительность меньше => тем не менее их результаты часто трактуют однозначно
ЛИТЕРАТУРУ НАДО АНАЛИЗИРОВАТЬ КРАЙНЕ АККУРАТНО!

ИССЛЕДОВАНИЕ НОВОГО СРЕДСТВА, УМЕНЬШАЮЩЕГО УРОВЕНЬ ГЛЮКОЗЫ КРОВИ ПРИ САХАРНОМ ДИАБЕТЕ
Цель: оценить эффективность нового лекарственного средства
Дизайн: рандомизированное исследование в 3 группах – плацебо, инсулин, инсулин+препарат. n1=10, n2=12, n3=40. Сравнение групп по концентрации глюкозы в крови, по частоте сердечно-сосудистых осложнений (инсульты, инфаркты, гангрены), по качеству жизни.
Результаты: Концентрация глюкозы в крови составила в группе плацебо 13(10, 16) {указана медиана и квартили}, в группе инсулина 6 (4, 8), в группе инсулин+ препарат 4 (5, 6). При попарном сравнении по Манну-Уитни значимости были такими: р(плацебо-инсулин) = 0,009, р(инсулин – инсулин+препарат) = 0,05; р(плацебо – инсулин+препарат) = 0,001.
Частота сердечно-сосудистых осложнений в группе плацебо составила 3 случая за время наблюдения, в группе инсулина – 1 случай, в группе инсулин+препарат – 5 случаев. Различия между группами не значимы (хи-квадрат р=0,38)
Результаты по опроснику качества жизни составили в группе плацебо 6±1,34 {чем больше тем лучше, шкала от 1 до 10}, в группе инсулина 9±2,15, в группе инсулин+препарат 9±0,94. При попарном сравнении t-критерием Стьюдента значимости были такими: р(плацебо-инсулин) = 0,03, р(инсулин – инсулин+препарат) = 0,6; р(плацебо – инсулин+препарат) = 0,01.
Дополнительно в исследовании приведены данные концентрации глюкозы до начала терапии в группе комбинированной терапии – 11(10, 12), и результаты сравнения по Манну-Уитни с окончанием исследования (р=0,005).

Хорош ли препарат???
Оцениваем цель и ее соответствие дизайну
Полнота описания групп исследования, популяции исследования
Конечные точки?
По каждому из сравнений:
Оценить тип зависимой переменной
Оценить ее распределение (если возможно)
Адекватна ли описательная статистика?
Адекватны ли графики?
Тот ли метод сравнения использован?
Учтена ли множественность сравнений (если есть)?
Верно ли интерпретировано?

ИССЛЕДОВАНИЕ НОВОГО СРЕДСТВА, УМЕНЬШАЮЩЕГО УРОВЕНЬ ГЛЮКОЗЫ КРОВИ ПРИ САХАРНОМ ДИАБЕТЕ
Цель: оценить эффективность нового лекарственного средства
Дизайн: рандомизированное исследование в 3 группах – плацебо, инсулин, инсулин+препарат. n1=10, n2=12, n3=40. Сравнение групп по концентрации глюкозы в крови, по частоте сердечно-сосудистых осложнений (инсульты, инфаркты, гангрены), по качеству жизни.
Результаты: Концентрация глюкозы в крови составила в группе плацебо 13(10, 16) {указана медиана и квартили}, в группе инсулина 6 (4, 8), в группе инсулин+ препарат 4 (5, 6). При попарном сравнении по Манну-Уитни значимости были такими: р(плацебо-инсулин) = 0,009, р(инсулин – инсулин+препарат) = 0,05; р(плацебо – инсулин+препарат) = 0,001.
Частота сердечно-сосудистых осложнений в группе плацебо составила 3 случая за время наблюдения, в группе инсулина – 1 случай, в группе инсулин+препарат – 5 случаев. Различия между группами не значимы (хи-квадрат р=0,38)
Результаты по опроснику качества жизни составили в группе плацебо 6±1,34 {чем больше тем лучше, шкала от 1 до 10}, в группе инсулина 9±2,15, в группе инсулин+препарат 9±0,94. При попарном сравнении t-критерием Стьюдента значимости были такими: р(плацебо-инсулин) = 0,03, р(инсулин – инсулин+препарат) = 0,6; р(плацебо – инсулин+препарат) = 0,01.
Дополнительно в исследовании приведены данные концентрации глюкозы до начала терапии в группе комбинированной терапии – 11(10, 12), и результаты сравнения по Манну-Уитни с окончанием исследования (р=0,005).

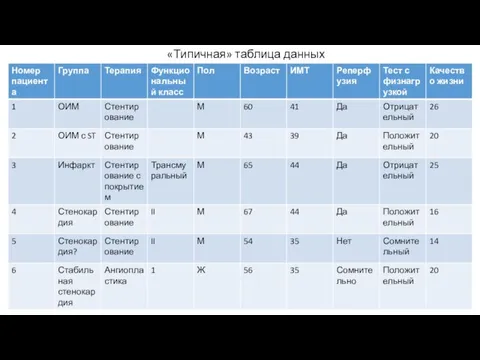
«Типичная» таблица данных

ПКТ – качество жизни после разных типов ангиопастики;
Качество жизни – основная зависимая переменная
Сколько факторов влияет?
Как сравнивать?
А еще – есть качество жизни через полгода и год, и рестенозы…

Дисперсионный анализ
Одномерный, однофакторный
Многофакторный
(оценивается соотношение дисперсий для каждого фактора и их взаимодействия)
Многомерный
(если зависимые переменные взаимодействуют)
Общая линейная модель!
Зависимая переменная – переменная отклика, измеряемая переменная, отражает исследуемое явление;
Независимая переменная – прочие переменные (факторы и ковариаты);
Фиксированный (постоянный) фактор – качественная или порядковая переменная изначально запланированная в исследовании;
Случайный фактор – измеренный/оцененный попутно в ходе исследования;
Ковариата – количественная переменная оказывающая влияние на зависимую переменную.

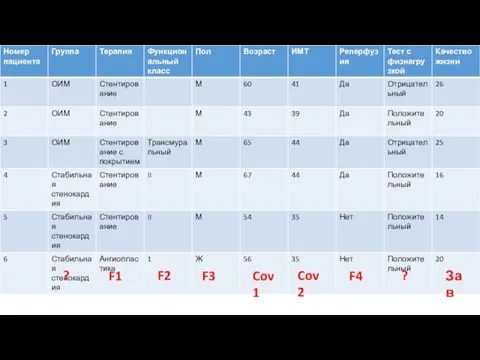
F1
F2
F3
F4
?
?
Зав
Cov 1
Cov 2

Общая линейная модель
где Y есть матрица, включающая описываемые измерения, В — матрица, включающая параметры, представляющие интерес для исследования, Х — матрица, включающая постоянные коэффициенты, и U — матрица случайных ошибок. Модели, в которых каждая координата вектора Х является целым числом (0 или 1) и обозначает групповую принадлежность, применяются при дисперсионном анализе. Модели, в которых Х является непрерывной числовой переменной, применяются при регрессионном анализе. Модели, в которых присутствуют оба вида значений Х, применяются при ковариационном анализе.
Смешанная линейная модель (включает в модель случайные факторы и вложенные измерения (nested data));
Обобщенная линейная модель (система уравнений включающая все возможные варианты переменных и взаимодействий.
Мало чувствительны к непараметричности данных! (интегрирование)
Непараметрических многофакторных методов НЕТ.

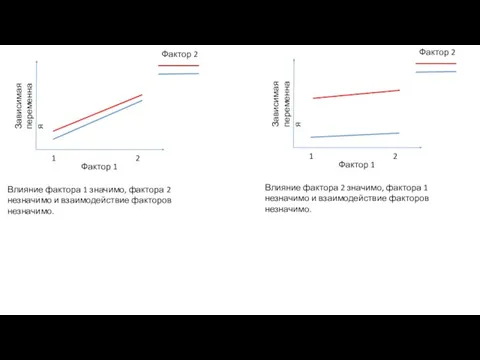
Фактор 1
Зависимая переменная
1
2
Фактор 2
Влияние фактора 1 значимо, фактора 2 незначимо и взаимодействие факторов незначимо.
Фактор 1
Зависимая переменная
1
2
Фактор 2
Влияние фактора 2 значимо, фактора 1 незначимо и взаимодействие факторов незначимо.

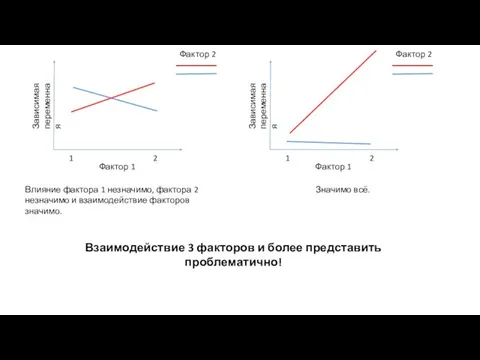
Фактор 1
Зависимая переменная
1
2
Фактор 2
Влияние фактора 1 незначимо, фактора 2 незначимо и взаимодействие факторов значимо.
Фактор 1
Зависимая переменная
1
2
Фактор 2
Значимо всё.
Взаимодействие 3 факторов и более представить проблематично!

Если в исследовании много различных параметров влияние которых на количественный показатель(-и) руководитель просит «посмотреть» – надо применять общую линейную модель в варианте многофакторного дисперсионного анализа
Если зависимых переменных много и получены они одним и тем же методом – надо провести между ними корреляционный анализ и если корреляция будет - надо применять общую линейную модель в варианте многомерного дисперсионного анализа
Если зависимую переменную измеряли в нескольких временных точках - надо применять общую линейную модель в варианте дисперсионного анализа с повторными измерениями
Если для каждого субьекта исследования нет точного числа, а есть оценка по нескольким измерениям (микрофотографии – для оценки количества неких клеток) – надо применять смешанную линейную модель со «вложением» данных (nested data – официального русского перевода нет!)
Если при всем этом число случаев в выборке мало, а зависимая переменная явно распределена непараметрически – надо молиться