Сферическая теория артикуляции Монсона

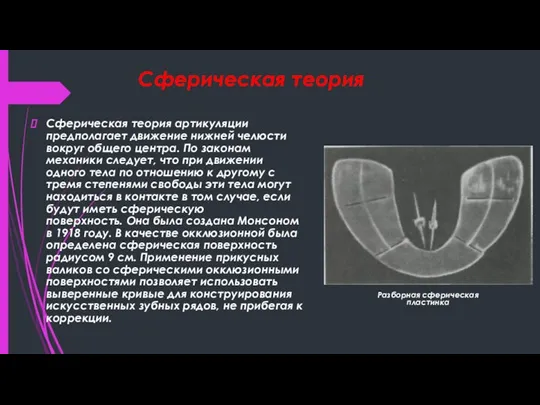
Сферическая теория
Сферическая теория артикуляции предполагает движение нижней челюсти вокруг общего центра. По законам механики следует, что при движении одного тела no отношению к другому с тремя степенями свободы эти тела могут находиться в контакте в том случае, если будут иметь сферическую поверхность. Она была создана Монсоном в 1918 году. В качестве окклюзионной была определена сферическая поверхность радиусом 9 см. Применение прикусных валиков со сферическими окклюзионными поверхностями позволяет использовать выверенные кривые для конструирования искусственных зубных рядов, не прибегая к коррекции.
Разборная сферическая пластинка

Требования теории
Общим требованием теории артикуляции является обеспечение множественного скользящего контакта между искусственными зубами в фазе жевательных движений. Из этой точки зрения наиболее правильная сферическая теория артикуляции разработанная в 1918 г. Монсоном. Она была подтверждена в трудах Gabera (1960), Hampel (1980), Б.Т.Черних и С.И.Хмелевского (1965) и пр.
Эти авторы применили при изучении строения жевательного аппарата и черепа данные точных наук (физики и математики) и установили, что сферическая теория артикуляции наиболее полно сравнительно с другими теориями, отображает сферические особенности строения зубочелюстной системы и всего черепа, а также сложные движения нижней челюсти. Представители сферической теории прежде всего отмечают, что по сферическим поверхностям легче проводить постановку искусственных зубов.

ОККЛЮЗИОННАЯ ПОВЕРХНОСТЬ
Проведенные клинические исследования доказали, что поверхностный контакт между прикусными шаблонами при перетирании пищи возможный, если их окклюзионные поверхности имеют сферическую форму, при этом для каждого пациента существует целый ряд диапазонов сферических поверхностей, которые обеспечивают контакты валиков.
Наличие этого диапазона указывает на то, что нет необходимости в определении радиусов индивидуальных окклюзионных поверхностей и дает возможность пациенту адаптироваться к протезам сконструированным в некоторой мере неверно. Ширина этого диапазона соответствует, адаптационным возможностям жевательного аппарата.

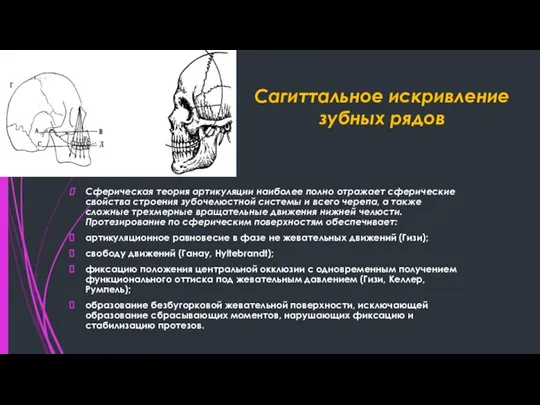
Сагиттальное искривление зубных рядов
Сферическая теория артикуляции наиболее полно отражает сферические свойства строения зубочелюстной системы и всего черепа, а также сложные трехмерные вращательные движения нижней челюсти. Протезирование по сферическим поверхностям обеспечивает:
артикуляционное равновесие в фазе не жевательных движений (Гизи);
свободу движений (Ганау, Hyltebrandt);
фиксацию положения центральной окклюзии с одновременным получе­нием функционального оттиска под жевательным давлением (Гизи, Келлер, Румпель);
образование безбугорковой жевательной поверхности, исключающей образование сбрасывающих моментов, нарушающих фиксацию и стабилизацию протезов.

ПРИ ПОЛНОМ ОТСУТСТВИИ ЗУБОВ
Протезирование больных с полной потерей зубьев необходимо проводить таким образом, чтобы не нарушать связей, которые образовались к потере зубов.
Если при определении центрального соотношения челюстей вместо протетической плоскости формировать сферические поверхности можно значительно повысить качество протезов у беззубых больных. Появляются возможности проверить контакты между прикусными валиками, а значит между искусственными зубами при перетирании пищи.
Применение прикусных валиков со сферическими поверхностями позволяют проверить контакты между валиками на этапе определения центральной окклюзии и использовать выверенные окклюзионные кривые для конструирования искусственных зубных рядов, которые не требуют коррекции.

ПРЕИМУЩЕСТВА СФЕРИЧЕСКОЙ ТЕОРИИ
Конструирование искусственных зубных рядов по сферическим поверхностям обеспечивает создание оптимального поля сил жевательного давления, что не вызывает быстрой атрофии твердых и мягких тканей протезного ложа. Протезирование по сферическим поверхностям обеспечивает:
артикуляционное равновесие в фазе не жевательных движений (Gysi); свободу движений (Hanau, Hyltebrandt);
фиксацию положения центральной окклюзии с одновременным получением функционального оттиска под жевательным давлением (Gysi, Keller, Rumpel);
образование безбугорковой жевательной поверхности (Fehr, Eichner и др.), исключающей образование сбрасывающих моментов, нарушающих фиксацию и стабилизацию протезов.

Поэтому протезирование по сферической поверхности рационально и показано:
при протезировании беззубых челюстей;
при наличии одного или нескольких естественных зубов; с целью изготовления шин при пародонтозе;
при коррекции окклюзионной поверхности естественных зубов для создания правильных артикуляционных взаимоотношений с искусственными зубами на противоположной челюсти;
для целенаправленного лечения при заболеваниях суставов.
Сторонники сферической теории прежде всего отмечают, что по сфере легче производить постановку искусственных зубов.

НЕДОСТАТКИ СФЕРИЧЕСКОЙ ТЕОРИИ
Изготовление стеновых шаблонов и валиков более трудоемко, чем восковых. Применение данной методики невозможно при наличии одиночных естественных зубов Основной недостаток методики заключается в том, что авторы стремились по в каждом отдельном случае получить индивидуальные окклюзионные кривые. Исследования Б. Р. Вайнштейна (1949) о применении сферических пластинок различных радиусов свидетельствуют о целесообразности использования сферической поверхности радиусом 148,2 см для оформления окклюзионных поверхностей прикусных валиков и последующей постановки искусственных зубов. Это значительно облегчило бы применение методики, гораздо легче проверять правильность формирования прикусных валиков, чем при наличии феномена формировать индивидуальные окклюзионные кривые, во-вторых, отпала бы необходимости пользоваться стеновыми прикусными валиками, в-третьих, формирование окклюзионных поверхностей, прикусных валиков можно было бы производить при наличии одиночных естественных зубов.

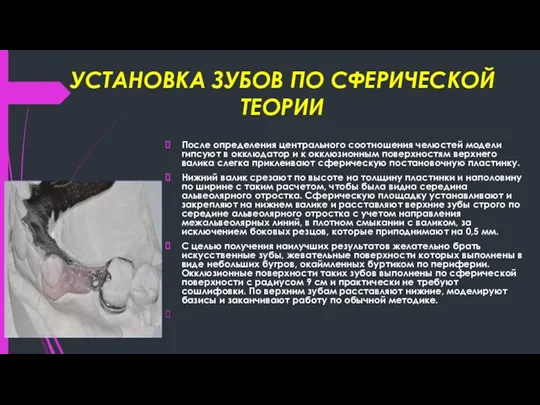
УСТАНОВКА ЗУБОВ ПО СФЕРИЧЕСКОЙ ТЕОРИИ
Постановка зубов по сферическим поверхностям улучшает фиксацию протезов, обеспечивает свободу жевательных движений, замедляет атрофические процессы в тканях протезного ложа.
После получения моделей готовят прикусные шаблоны. Валики со сферическими поверхностями делают из смеси расплавленного воска с песком, заливая смесь в эластичную форму, полученную по гипсовым столбикам. Считают, что больше контактов между зубами бывает при радиусе сферы, равной 9 см. Такой радиус создают и на окклюзионных валиках. В переднем участке, равном по ширине четырем резцам, формируют горизонтальную постановочную площадку, параллельную зрачковой линии. При симметричном наклоне межальвеолярных линий применяют разборную пластинку, состоящую из трех частей: двух сферических боковых и фронтальной горизонтальной площадки, которая устанавливается между линиями клыков, или цельную, если наклон межальвеолярных линий незначительный.

УСТАНОВКА ЗУБОВ ПО СФЕРИЧЕСКОЙ ТЕОРИИ
После определения центрального соотношения челюстей модели гипсуют в окклюдатор и к окклюзионным поверхностям верхнего валика слегка приклеивают сферическую постановочную пластинку.
Нижний валик срезают по высоте на толщину пластинки и наполовину по ширине с таким расчетом, чтобы была видна середина альвеолярного отростка. Сферическую площадку устанавливают и закрепляют на нижнем валике и расставляют верхние зубы строго по середине альвеолярного отростка с учетом направления межальвеолярных линий, в плотном смыкании с валиком, за исключением боковых резцов, которые приподнимают на 0,5 мм.
С целью получения наилучших результатов желательно брать искусственные зубы, жевательные поверхности которых выполнены в виде небольших бугров, окаймленных буртиком по периферии. Окклюзионные поверхности таких зубов выполнены по сферической поверхности с радиусом 9 см и практически не требуют сошлифовки. По верхним зубам расставляют нижние, моделируют базисы и заканчивают работу по обычной методике.

ЛИЦЕВАЯ ДУГА
Для оформления окклюзионных поверхностей на восковых валиках и определения правильной протетической сферической поверхности Б.Т. Черных и С.И. Хмелевским (1965) предложено специальное устройство – лицевая дуга, состоящая из внеротовой дуги – линейки и внутриротовых съемных формирующих пластинок, фронтальная часть которых плоская, а дистальные отделы имеют сферическую поверхность различных радиусов.
Лицевая дуга позволяет оформлять окклюзионные валики со сферическими поверхностями различной кривизны, с соответствием расположения по носоушной и зрачковой линии.