Почему компьютер считает?

Обоснуйте возможность записи чисел в двоичной форме?
Обоснуйте возможность записи символов в двоичной форме?
Почему сложение является уникальной операцией в двоичной арифметике?
Проблемные вопросы

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
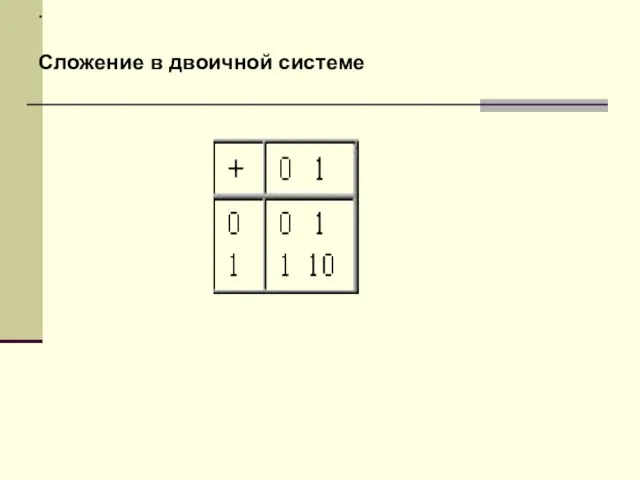
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Почему люди пользуются десятичной системой, а компьютеры — двоичной?

Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю.
Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения

Пример: Переведем число 75 из десятичной системы в двоичную:
Ответ: 7510 = 1 001 0112

Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?
Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе.
Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой.

Пример. Переведем число 0,36 из десятичной системы в двоичную:
Для чисел, имеющих как целую, так и дробную
части, перевод из десятичной системы счисления
в другую осуществляется отдельно для целой и
дробной частей по правилам, указанным выше.

Запись символов в двоичной форме
Существуют специальные таблицы в которых каждый символ имеет десятичный код.
Например, лат. А имеет код 65
Для записи символов в десятичной форме
Необходимо его десятичный код записать в двоичной форме:
65 = 010000012

.
Сложение в двоичной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.

ВЫЧИТАНИЕ в двоичной системе
Пример: Выполнить вычитание 10-5 в двоичной арифметике:
10=10102
5=1012=01012 →10102+1=10112
10102+10112=101012
В результате старший разряд отбрасываем.
Ответ: 1012

Умножение и деление
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Пример 7. Перемножим числа 5 и 6.
Ответ: 5*6 = 3010 = 111102.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30;

Разделим число 35 на число 14.
Ответ: 35 : 14 = 2,510 = 10,12
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5; Деление двоичных чисел сводится к вычитанию двоичных чисел,
а вычитание двоичных чисел можно выполнить через сложение.