Содержание
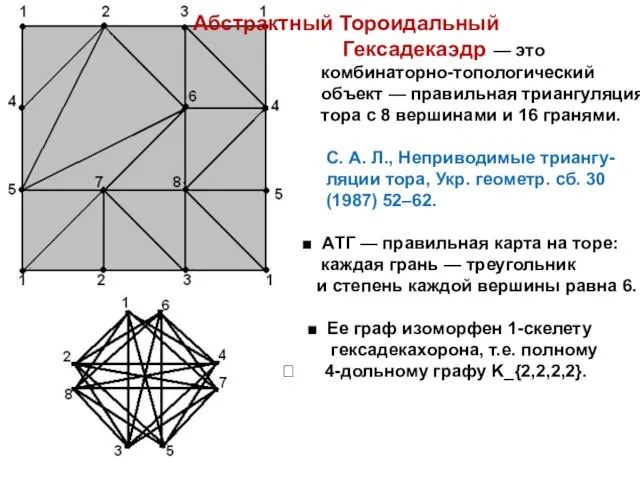
- 2. Абстрактный Тороидальный Гексадекаэдр — это комбинаторно-топологический объект — правильная триангуляция тора с 8 вершинами и 16
- 3. Все ее автоморфизмы найдены при помощи компьютера: С. А. Л., Перечисление в явном виде всех автоморфизмов
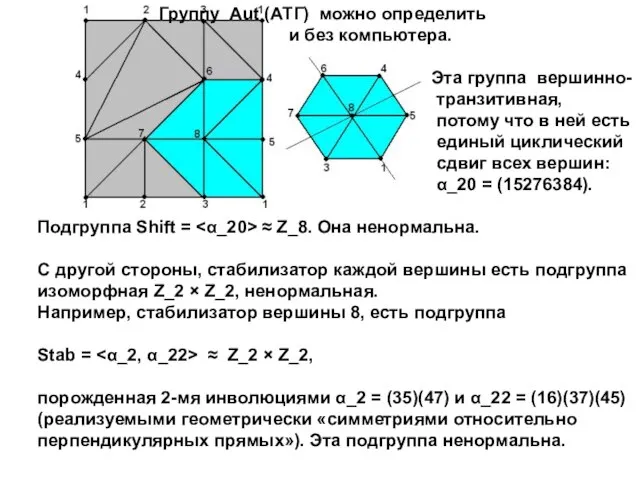
- 4. Группу Aut (АТГ) можно определить и без компьютера. Эта группа вершинно- транзитивная, потому что в ней
- 5. Таким образом, группа Aut (АТГ) может быть порождена так: Aut (АТГ) = = (Z_2 × Z_2)
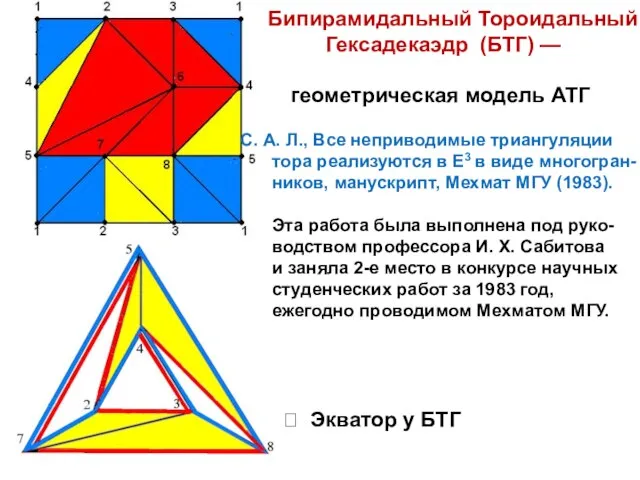
- 6. Бипирамидальный Тороидальный Гексадекаэдр (БТГ) — геометрическая модель АТГ С. А. Л., Все неприводимые триангуляции тора реализуются
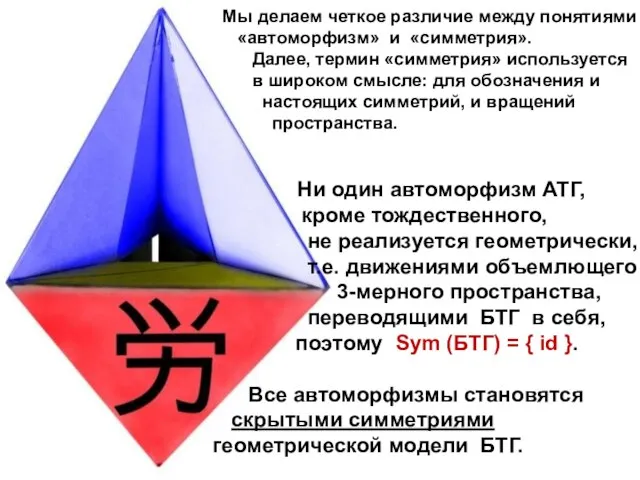
- 8. Мы делаем четкое различие между понятиями «автоморфизм» и «симметрия». Далее, термин «симметрия» используется в широком смысле:
- 9. Хáролд Скотт МакДóналд («Доналд») Кокстер (1907—2003). Парадигма Кокстера Парадигма Кокстера «групп и геометрии» — это целостная
- 10. Борьба со скрытыми симметриями — путь претворения в жизнь парадигмы Кокстера. Многогранные реализации групп правильных карт
- 11. Борьба со скрытыми симметриями — путь претворения в жизнь парадигмы Кокстера. Новая идея: Но что, если
- 12. Тор Клиффорда: (x_1)² + (x_2)² = 1 = (x_3) ² + (x_4)². Для 2-мерного тора более
- 13. С. А. Л., Polyhedral suspensions of arbitrary genus, Graphs & Combinatorics, 26 (2010), в печати. Теорема
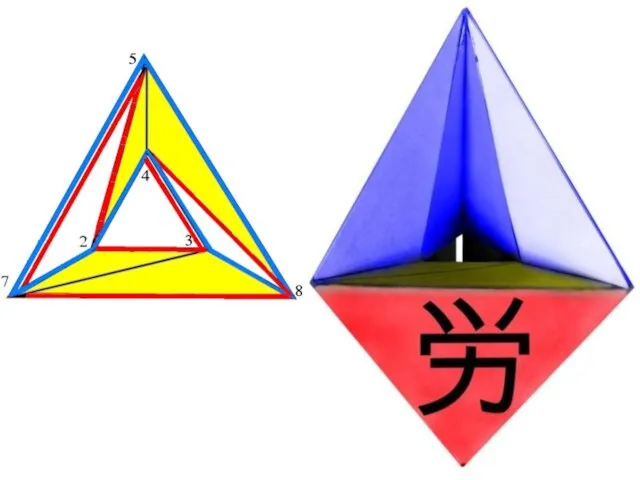
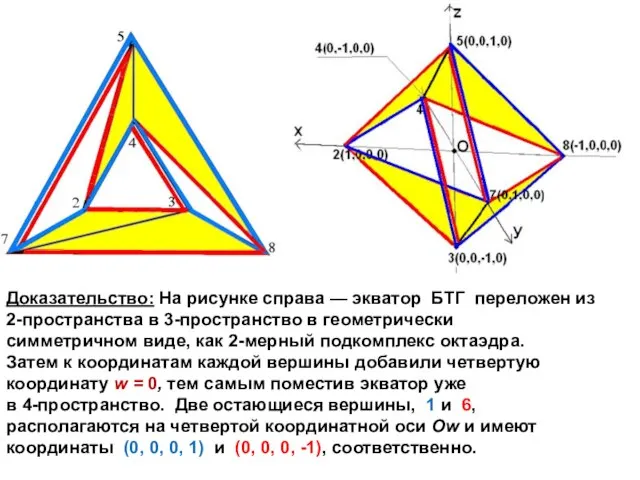
- 14. Доказательство: На рисунке справа — экватор БТГ переложен из 2-пространства в 3-пространство в геометрически симметричном виде,
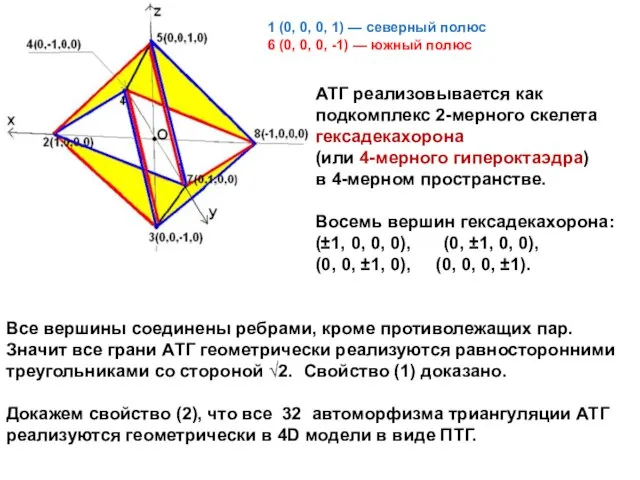
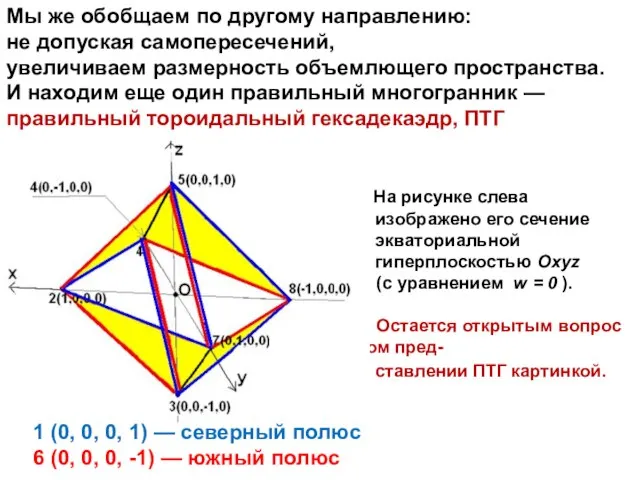
- 15. 1 (0, 0, 0, 1) — северный полюс 6 (0, 0, 0, -1) — южный полюс
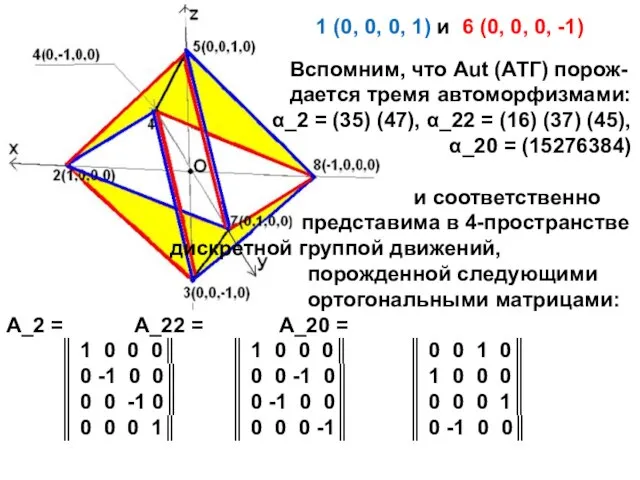
- 16. 1 (0, 0, 0, 1) и 6 (0, 0, 0, -1) Вспомним, что Aut (АТГ) порож-
- 17. Таким образом, получено точное представление группы Aut (АТГ) степени 4. Где —специальная ортогональная группа степени 4,
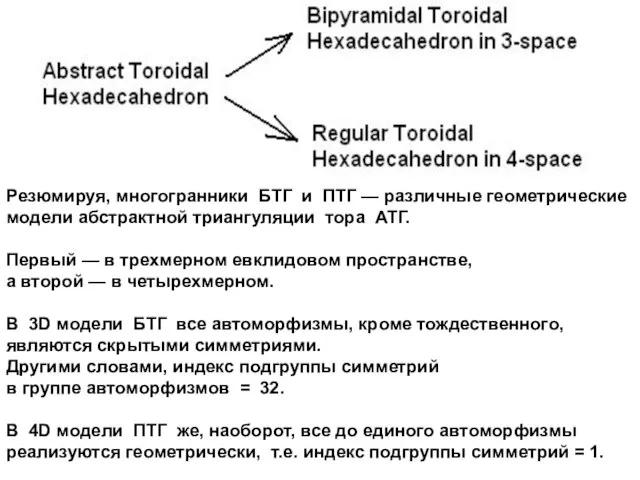
- 18. Резюмируя, многогранники БТГ и ПТГ — различные геометрические модели абстрактной триангуляции тора АТГ. Первый — в
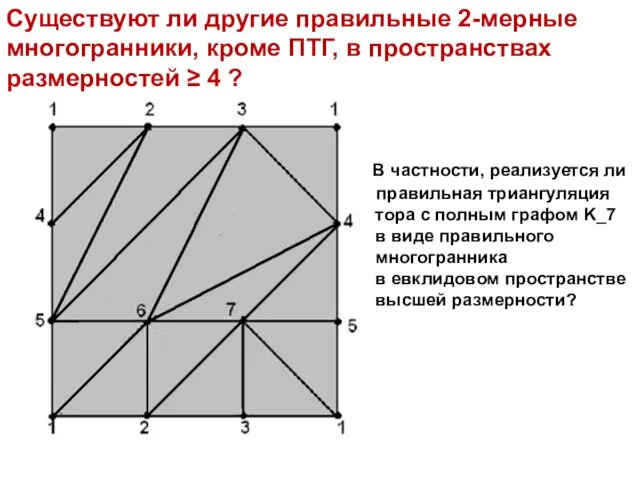
- 19. Открытые вопросы ■ Существуют ли другие правильные 2-мерные многогранники, кроме ПТГ, в (евклидовом) пространстве размерности 4
- 20. Существуют ли другие правильные 2-мерные многогранники, кроме ПТГ, в пространствах размерностей ≥ 4 ? В частности,
- 21. Теорема (Рингель и Янгс): Для каждого целого положительного n такого, что (n–3)(n–4) делится нацело на 12,
- 22. Реализуются ли при этом геометрически все автоморфизмы триангуляции? Оказывается, будет вершинно-транзитивной группа автоморфизмов любой триангуляции тора,
- 23. Итак, что же такое правильный многогранник?? Что касается 2-мерных многогранников в евклидовом n-мерном пространстве, тот заслуживает
- 24. Такое определение правильного многогранника предполагает более широкий класс многогранников, чем в классическом смысле. Исторически, когда ограничивались
- 25. 6 марта, 2009 г. Запуск ракеты Дельта II с Кеплером на поиск планет, в некотором отношении
- 26. Многогранники Кеплера-Пуансо (не типа сферы!) Малый звездчатый додекаэдр Большой звездчатый додекаэдр Большой додекаэдр Большой икосаэдр В
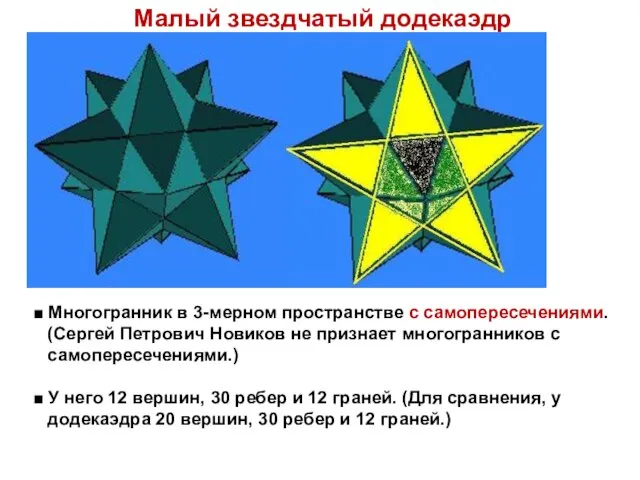
- 27. Малый звездчатый додекаэдр ■ Многогранник в 3-мерном пространстве с самопересечениями. (Сергей Петрович Новиков не признает многогранников
- 28. Мы же обобщаем по другому направлению: не допуская самопересечений, увеличиваем размерность объемлющего пространства. И находим еще
- 30. Скачать презентацию















 Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике
Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике England
England Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер»
Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер» Культура и традиции мордовского народа
Культура и традиции мордовского народа Почему нельзя не проветривать кабинет?
Почему нельзя не проветривать кабинет? Новый взгляд на экономическую географию
Новый взгляд на экономическую географию Презентация на тему Внутреннее строение млекопитающих
Презентация на тему Внутреннее строение млекопитающих Оживший Бог войны Арес - неукротимый бог войны
Оживший Бог войны Арес - неукротимый бог войны Гендерная статистика ЕГЭ по техническим предметам
Гендерная статистика ЕГЭ по техническим предметам Законы сохранения в механике
Законы сохранения в механике РДУ-99. Его значение и применение
РДУ-99. Его значение и применение India - English Transit
India - English Transit Презентация на тему Драгоценные камни
Презентация на тему Драгоценные камни 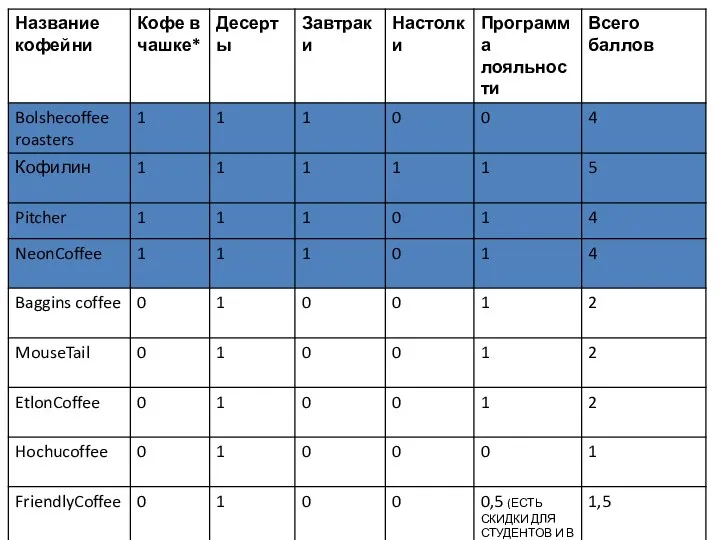 4. карта позиционирования, конкуренты_Шашина_3ГИВ13
4. карта позиционирования, конкуренты_Шашина_3ГИВ13 Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов
Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн
Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн Конкурс среди молодых семей «Семь Я»
Конкурс среди молодых семей «Семь Я» Ваше название
Ваше название Изготовление аксессуара Цветок
Изготовление аксессуара Цветок Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений
Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ»
Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ» Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения
Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения Специальность «Режиссер шоу-программ и театрализованных представлений»
Специальность «Режиссер шоу-программ и театрализованных представлений» Врачебный диагноз
Врачебный диагноз Привлечение средств от приносящей доход деятельности
Привлечение средств от приносящей доход деятельности Кукольный театр
Кукольный театр Большой, красивый, уютный.
Большой, красивый, уютный. Париж
Париж