Содержание
- 2. ЗАДАЧА ИЗ ДРЕВНЕГО ЕГИПТА « Найти стороны поля, имеющего форму прямоугольника, если его площадь 12, а
- 3. В ОДНОЙ ИЗ ВАВИЛОНСКИХ ЗАДАЧ ТАК ЖЕ ТРЕБОВАЛОСЬ ОПРЕДЕЛИТЬ ДЛИНУ ПРЯ-МОУГОЛЬНОГО ПОЛЯ И ЕГО ШИРИНУ :
- 4. СОСТАВИМ СИСТЕМУ УРАВНЕНИЙ
- 5. Теперь уравнение можно записать так: Мы пришли к квадратному уравнению, которое умели решать и египтяне. Не
- 6. Бхаскара Агарья (1114-1185) Индийский математик и астроном. Занимался вопросами алгебры, тригонометрии, геометрии и комбинаторики. В его
- 7. ЗАДАЧА БХАСКАРЫ На две партии разбившись, Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело
- 8. РЕШЕНИЕ: Ответ: 48 или 16 обезьян
- 9. АЛЬ-ХОРЕЗМИ. Наибольших успехов в математике достиг согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом из Хорезма
- 10. Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы
- 11. - дискриминант квадратного уравнения Возможны 3 случая: - корней нет - один корень
- 12. №1. Решите уравнения: - два корня Ответ:
- 13. Ответ: корней нет корней нет. Ответ:
- 14. Ответ: нет корней Решите квадратное уравнение:
- 16. ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ С ЧЕТНЫМ ВТОРЫМ КОЭФФИЦИЕНТОМ Решаем упражнения из учебника: №534 (а, г, е,
- 17. УСТАНОВИТЕ СВЯЗЬ МЕЖДУ КВАДРАТНЫМ УРАВНЕНИЕМ И СПОСОБАМИ ЕГО РЕШЕНИЯ
- 18. КРОССВОРД 1. Уравнение вида ах²+вх+с=о 2.Квадратные уравнения, у которых первый коэффициент равен 1. 3. Уравнения с
- 20. Скачать презентацию

















 Межнациональные отношения
Межнациональные отношения Тест по теме: трудовой договор
Тест по теме: трудовой договор Преподаватель физкультуры: Киселева Светлана Викторовна МОУ СОШ 9.
Преподаватель физкультуры: Киселева Светлана Викторовна МОУ СОШ 9. Приемы компрессии текста
Приемы компрессии текста  Декоративные георгины
Декоративные георгины «Разработка и апробация моделей центров сертификации профессиональных квалификаций и экспертно-методического центра в отрасли м
«Разработка и апробация моделей центров сертификации профессиональных квалификаций и экспертно-методического центра в отрасли м Значение лесов
Значение лесов Презентация+_Локально_нормативные+акты+организации_
Презентация+_Локально_нормативные+акты+организации_ Электронные таблицы 10 класс
Электронные таблицы 10 класс Статья 5. Никто не должен подвергаться пыткам или жестоким, бесчеловечным или унижающим достоинство обращению и наказанию
Статья 5. Никто не должен подвергаться пыткам или жестоким, бесчеловечным или унижающим достоинство обращению и наказанию Система экономиина масштабах для участников IT-кластера в Ярославской области
Система экономиина масштабах для участников IT-кластера в Ярославской области Народное музыкальное творчество
Народное музыкальное творчество Пионеры – герои во время Великой Отечественной войне
Пионеры – герои во время Великой Отечественной войне Реализация технологии деятельностного подхода на уроках в начальной школе
Реализация технологии деятельностного подхода на уроках в начальной школе Эксклюзив C&W
Эксклюзив C&W Модуль 4Сущность и формы познания
Модуль 4Сущность и формы познания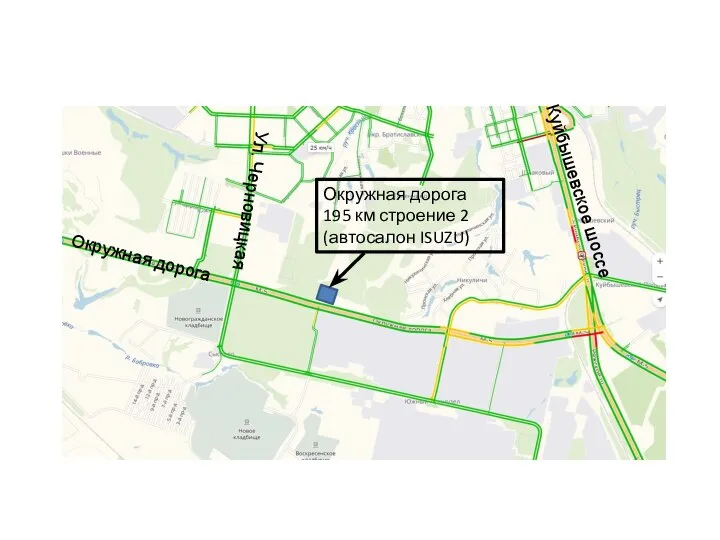 Окружная дорога 195 км строение 2 (автосалон ISUZU)
Окружная дорога 195 км строение 2 (автосалон ISUZU) Как создать эффективную схему работы финансовой службы и построить правильную систему мотивации
Как создать эффективную схему работы финансовой службы и построить правильную систему мотивации Кадровое бюро «охота»
Кадровое бюро «охота» Кабінет
Кабінет Фильтра Bosch
Фильтра Bosch Возрастные этапы становления социально-профессионального самоопределения
Возрастные этапы становления социально-профессионального самоопределения Мягконабивная игрушка Домовой
Мягконабивная игрушка Домовой Безлесные зоны юга России
Безлесные зоны юга России АДАПТАЦИЯ ПРИНЦИПОВ РЕГУЛИРОВАНИЯ К СОВРЕМЕННЫМ ЭКОНОМИЧЕСКИМ УСЛОВИЯМ
АДАПТАЦИЯ ПРИНЦИПОВ РЕГУЛИРОВАНИЯ К СОВРЕМЕННЫМ ЭКОНОМИЧЕСКИМ УСЛОВИЯМ Поклонение
Поклонение Принципи, шляхи й засоби адаптації європейської системи вищої освіти у вищу освіту України
Принципи, шляхи й засоби адаптації європейської системи вищої освіти у вищу освіту України Субъективная сторона преступления
Субъективная сторона преступления