Сложение гармонических колебаний

1. ВЕКТОРНАЯ
ДИАГРАММА (I)
Сложение гармонических колебаний одного направления облегчается и
становится наглядным, если изображать колебания графически в виде
векторов на плоскости. Такой способ называется векторной диаграммой.
Из точки 0, взятой на оси x отложим вектор
длины А, образующий с осью угол
Если привести этот вектор во вращение с
угловой скоростью то координата
конца вектора будет изменяться по закону
Следовательно, проекция
конца вектора на ось x будет
совершать гармонические
колебания с амплитудой, равной
длине вектора циклической
частотой и начальной фазой
равной углу, образуемому
вектором с осью x в начальный момент времени.

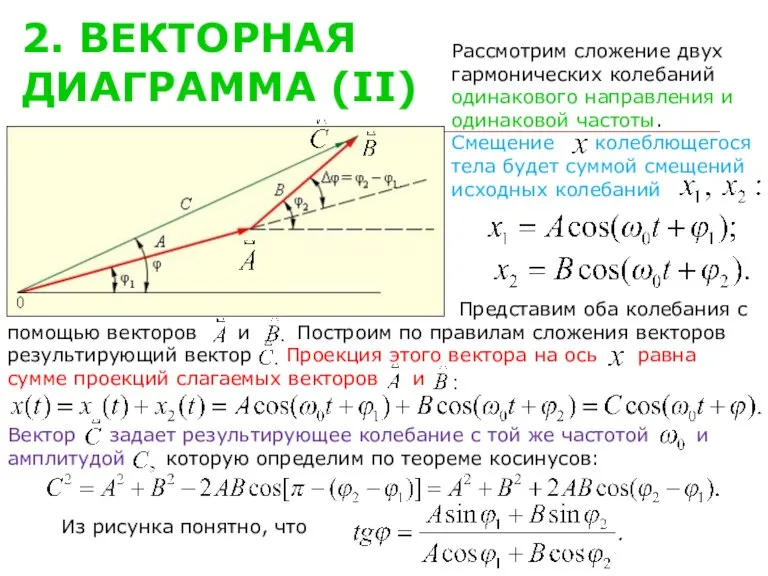
2. ВЕКТОРНАЯ ДИАГРАММА (II)
Рассмотрим сложение двух
гармонических колебаний
одинакового направления и
одинаковой частоты.
Смещение колеблющегося
тела будет суммой смещений
исходных колебаний
Представим оба колебания с
помощью векторов и Построим по правилам сложения векторов
результирующий вектор Проекция этого вектора на ось равна
сумме проекций слагаемых векторов и
Вектор задает результирующее колебание с той же частотой и
амплитудой которую определим по теореме косинусов:
Из рисунка понятно, что

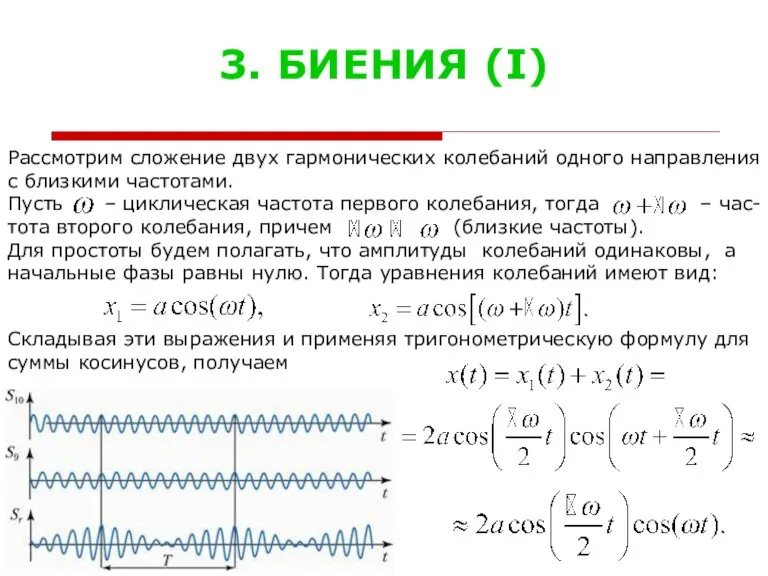
3. БИЕНИЯ (I)
Рассмотрим сложение двух гармонических колебаний одного направления
с близкими частотами.
Пусть – циклическая частота первого колебания, тогда – час-
тота второго колебания, причем (близкие частоты).
Для простоты будем полагать, что амплитуды колебаний одинаковы, а
начальные фазы равны нулю. Тогда уравнения колебаний имеют вид:
Складывая эти выражения и применяя тригонометрическую формулу для
суммы косинусов, получаем

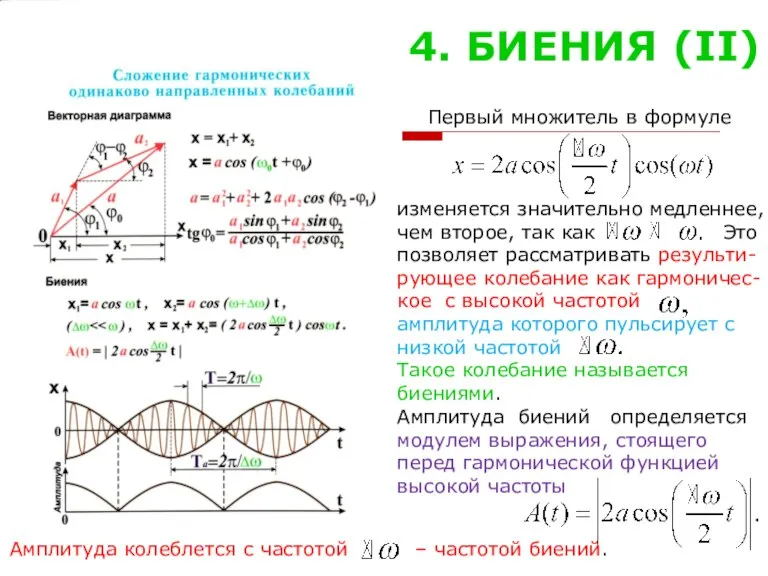
4. БИЕНИЯ (II)
Первый множитель в формуле
изменяется значительно медленнее, чем второе, так как Это
позволяет рассматривать результи-рующее колебание как гармоничес-кое с высокой частотой амплитуда которого пульсирует с низкой частотой
Такое колебание называется биениями.
Амплитуда биений определяется модулем выражения, стоящего перед гармонической функцией высокой частоты
Амплитуда колеблется с частотой – частотой биений.

5. СЛОЖЕНИЕ ВЗАИМНО
ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ
Пусть частица участвует одновременно в двух взаимно перпендикулярных
колебаниях одной частоты. Пусть колебания вдоль оси происходят с
нулевой начальной фазой, а вдоль оси со сдвигом по фазе на
Тогда уравнения колебаний примут вид:
Чтобы получить уравнение траектории в явном виде исключим время
Из первого уравнения следует, что
Подставляя синус и косинус в формулу
для получим:
Уединяя иррациональность и возводя в квадрат, придем к уравнению
которое представляет собой
уравнение эллипса. Полуоси
этого эллипса в общем случае
не совпадают с осями координат.

6. ДВИЖЕНИЕ ПО ПРЯМОЙ
Определим форму траектории результирующего колебания для некоторых частных случаев.
Пусть В этом случае общее уравнение траектории
принимает вид
Движение
является гармоническим
колебанием вдоль прямой
с амплитудой
2. Пусть В этом случае
Траектория является прямой, лежа-
щей во 2-м и 4-м квадрантах.

7. ДВИЖЕНИЕ
ПО ЭЛЛИПСУ
При общее
уравнение траектории
принимает вид
Это уравнение эллипса, приведенного
к координатным осям, причем полуоси
эллипса равны соответствующим
амплитудам колебаний.
При
движение против
часовой стрелки.
При
движение по
часовой стрелке

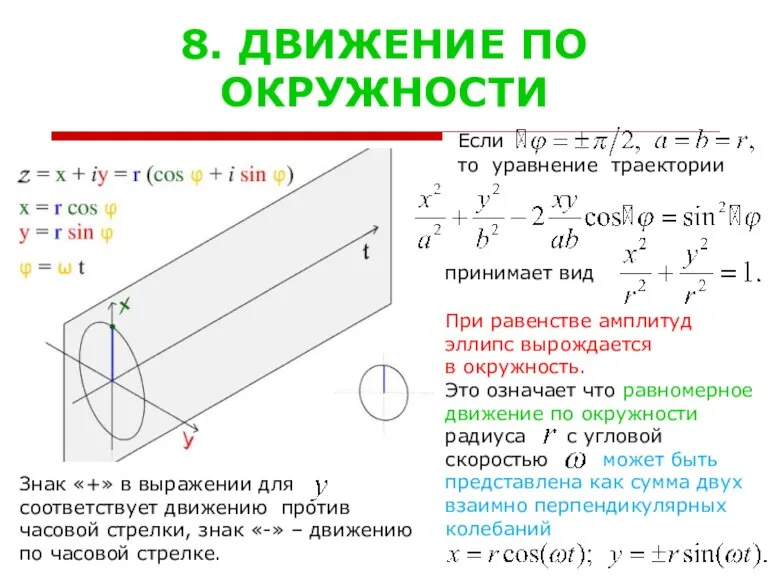
8. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Если
то уравнение траектории
Знак «+» в выражении для
соответствует движению против часовой стрелки, знак «-» – движению по часовой стрелке.
принимает вид
При равенстве амплитуд
эллипс вырождается
в окружность.
Это означает что равномерное
движение по окружности
радиуса с угловой
скоростью может быть
представлена как сумма двух
взаимно перпендикулярных
колебаний