Содержание
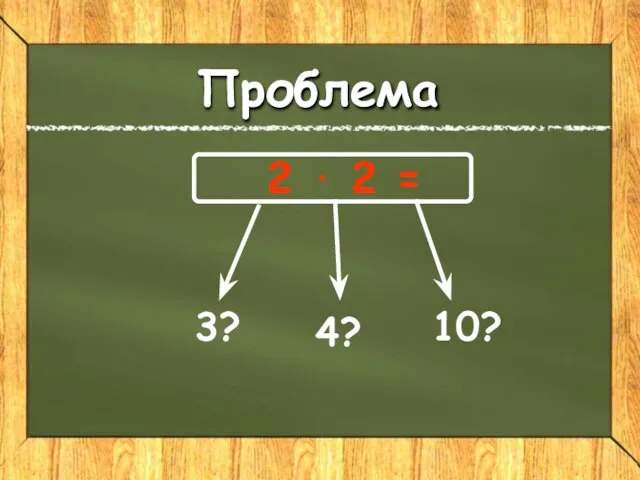
- 2. 2 ⋅ 2 = 3? 4? 10? Реши проблему Проблема
- 3. Очевидное и невероятное Очевидно: 2·2=4 Невероятно: 2·2=10 Гипотеза: Не всегда очевидное является истиной, а невероятное -
- 4. Изучение археологических “записок” времен палеолита на кости, камне, дереве показало, что люди стремились группировать предметы по
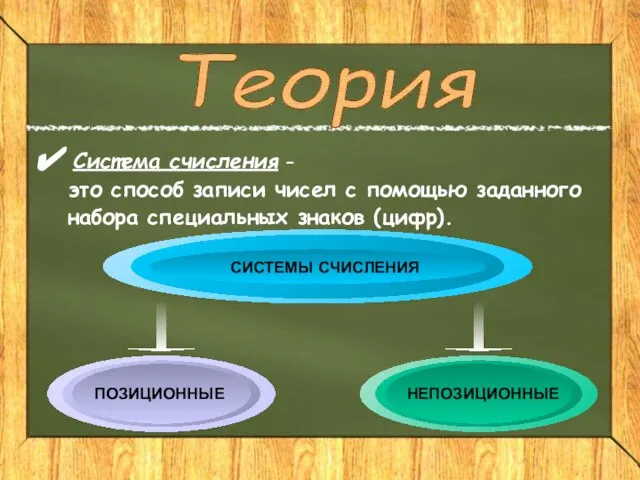
- 5. Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр). СИСТЕМЫ СЧИСЛЕНИЯ
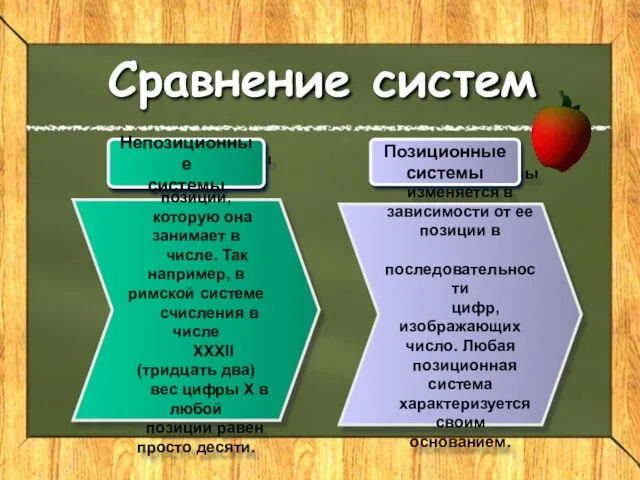
- 6. вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная
- 7. Вавилонская система счисления Является комбинацией шестидесятеричной и десятичной систем с применением позиционного принципа; используется всего два
- 8. Египет Число 1 245 386 Главный источник знаний о египетской числовой системе – папирус Райнда. Для
- 9. Египетская нумерация ЭТО ИЕРОГЛИФЫ
- 10. У ацтеков и майя, населявших американский континент и создавших там высокую культуру, почти полностью уничтоженную испанскими
- 11. В середине V в. до н. э. появилась запись чисел нового типа, так называемая алфавитная нумерация
- 12. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с
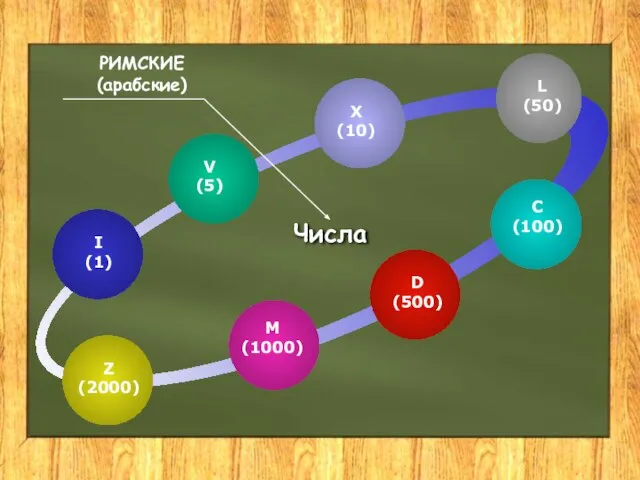
- 13. Римская нумерация Эта система непозиционная. В ней цифры записываются слева направо. Если слева записана меньшая цифра,
- 14. Это, самая распространенная на сегодняшний день нумерация, которой мы пользуемся в настоящее время. Применяемые в настоящее
- 15. Числа РИМСКИЕ (арабские) I (1) V (5) X (10) D (500) M (1000) Z (2000) L
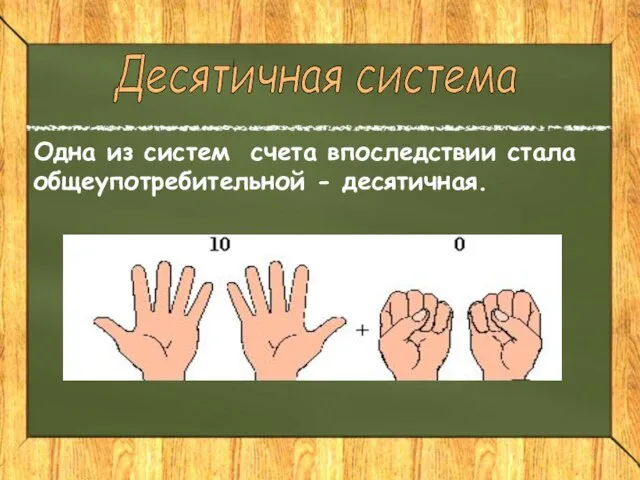
- 16. Десятичная система Одна из систем счета впоследствии стала общеупотребительной - десятичная.
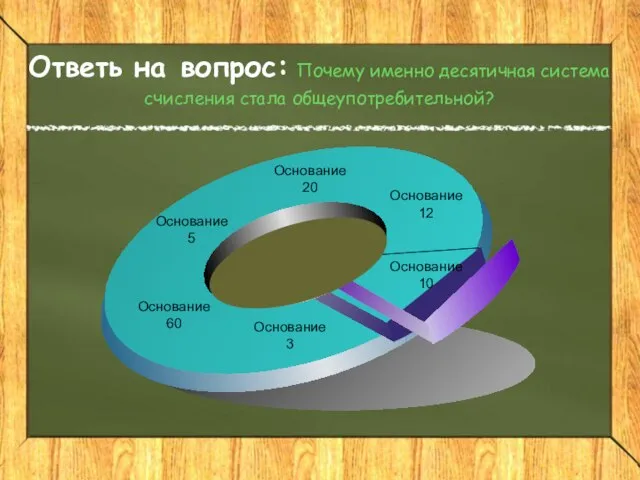
- 17. Основание 5 Основание 60 Основание 3 Основание 20 Основание 12 Основание 10 Ответь на вопрос: Почему
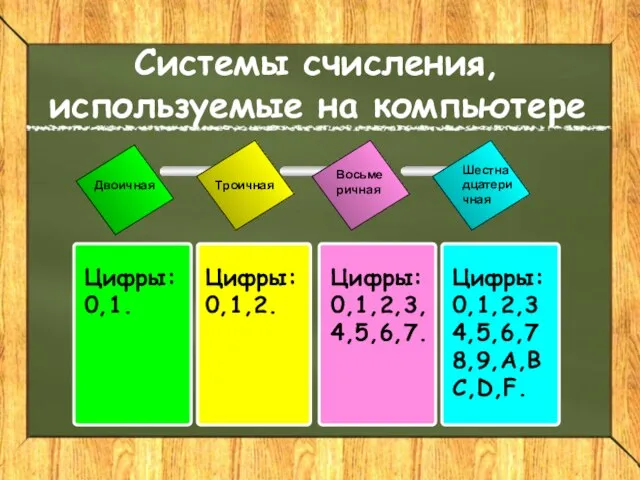
- 18. Двоичная Восьме ричная Шестна дцатери чная Троичная Цифры: 0,1. Цифры: 0,1,2. Цифры: 0,1,2,3,4,5,6,7. Цифры: 0,1,2,34,5,6,78,9,A,BC,D,F. Системы
- 19. 10000000001 двоичная 10000000001 Числа в разных системах счисления 2 0 0 1 4 0 1 восьмеричная
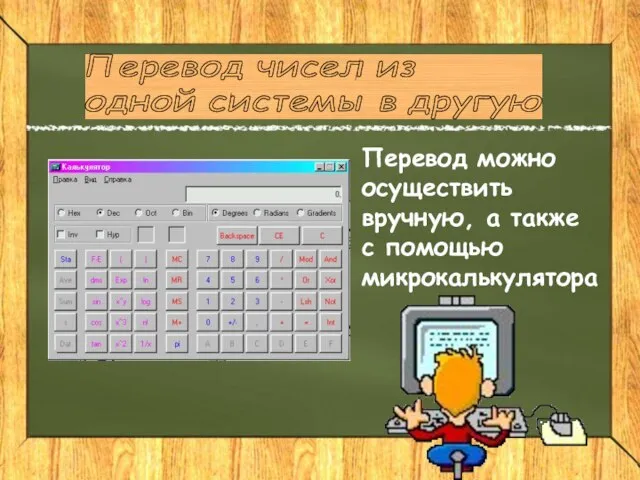
- 20. Перевод чисел из одной системы в другую Перевод можно осуществить вручную, а также с помощью микрокалькулятора
- 21. А очень любознательные могут разгадать кроссворд Не хочешь ли выполнить задание? Задание
- 22. Вывод 2 · 2 = 4 – равенство верно в десятичной системе, но ложно в двоичной
- 23. Средняя школа №2 Для углубления знаний по этой теме используй литературу: Энциклопедический словарь юного математика.- М.:
- 24. Средняя школа №2 Для углубления знаний по этой теме используй также Web ресурсы: http://www.internet-school.ru/Enc.ashx?folder=265&item=3693 http://sbiryukova.narod.ru/Seminar_03_04/Sem_5-03-04/Mat_dr_Ind_Belousova_5_04.htm http://www.krugosvet.ru/articles/17/1001738/0001237g.htm
- 26. Скачать презентацию















 архитектура эпохи возрождения
архитектура эпохи возрождения Систематика: RFID-решения для вашего бизнеса
Систематика: RFID-решения для вашего бизнеса Знатоки прав. Всероссийский День правовой помощи детям викторина
Знатоки прав. Всероссийский День правовой помощи детям викторина Санаторий Сосновый бор - филиал АО РЖД-здоровье. Кировская область
Санаторий Сосновый бор - филиал АО РЖД-здоровье. Кировская область Основы графической грамоты
Основы графической грамоты Номенклатура дел
Номенклатура дел флагман мирового производства клинкера
флагман мирового производства клинкера Виды промежуточных колонн в конструкции скважины
Виды промежуточных колонн в конструкции скважины Тропы
Тропы США в XIX веке
США в XIX веке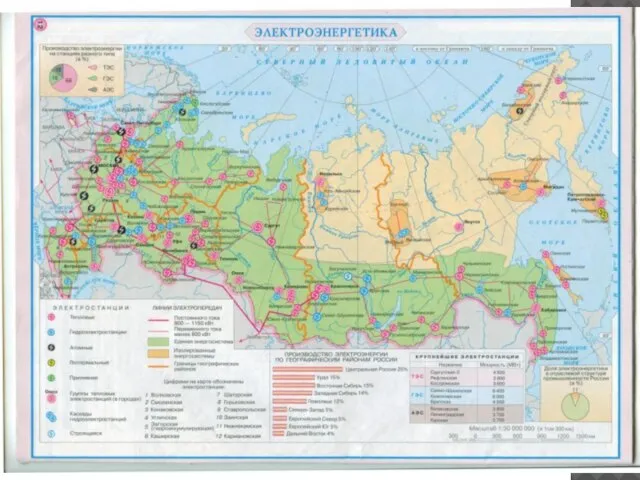 Направление нетрадиционной энергетики, основанное на непосредственном использовании солнечного излучения для получения энергии
Направление нетрадиционной энергетики, основанное на непосредственном использовании солнечного излучения для получения энергии Сказочный образ в картинах В.Васнецова.
Сказочный образ в картинах В.Васнецова. SMS Alert Gateway Техническая информация
SMS Alert Gateway Техническая информация Очень краткий гид по ВКР
Очень краткий гид по ВКР Проект “Диванный Trip”
Проект “Диванный Trip” Оценка ценных бумаг. Тема № 8
Оценка ценных бумаг. Тема № 8 Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм
Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм Mon animal
Mon animal Презентація
Презентація Переход на новые образовательные стандарты обучения в начальной школе
Переход на новые образовательные стандарты обучения в начальной школе Бирюза
Бирюза Опыт работы начальной школы
Опыт работы начальной школы Политические основы конституционного строя
Политические основы конституционного строя Реформы Петра I
Реформы Петра I МОУ СОШ № 4 . г. Всеволожск Ленинградская область Тема. Дисциплина Ученица 7 класса «Б» Матвейчук Антонина Учитель Потапова О.Н.
МОУ СОШ № 4 . г. Всеволожск Ленинградская область Тема. Дисциплина Ученица 7 класса «Б» Матвейчук Антонина Учитель Потапова О.Н. Sillamäe Vanalinna Kool 2.03.2011 Sofya Shesterneva «II мировая война в цифрах»
Sillamäe Vanalinna Kool 2.03.2011 Sofya Shesterneva «II мировая война в цифрах» Безопасность работы и конфиденциальность информации в АСУ РСО. - презентация
Безопасность работы и конфиденциальность информации в АСУ РСО. - презентация Базовий сметанний соус
Базовий сметанний соус