Слайд 2Цель урока:
Закрепить умения применять теорему Пифагора и теорему, обратную теореме Пифагора, при

решении задач.
Слайд 3План урока:
Повторение вопросов теории, решение задач по готовым чертежам.
История теоремы Пифагора, различные

доказательства теоремы Пифагора. (Сообщения)
Решение практических и древних задач
Проверочная работа с самоконтролем
Слайд 4Формулировка теоремы Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
а
b
с

Слайд 5Формулировка теоремы, обратной теореме Пифагора
Если квадрат одной стороны треугольника
равен сумме квадратов

двух других сторон,
то треугольник прямоугольный.
Слайд 6Решите задачу
Дано: ABCD – ромб, АС = 12 см, BD =
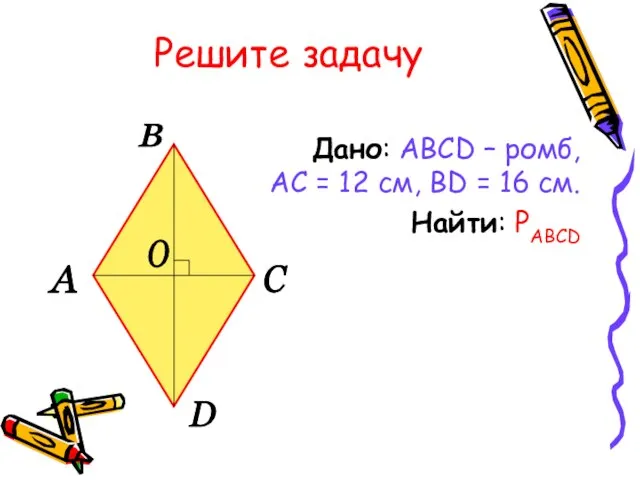
16 см.
Найти: PABCD
A
B
C
D
O
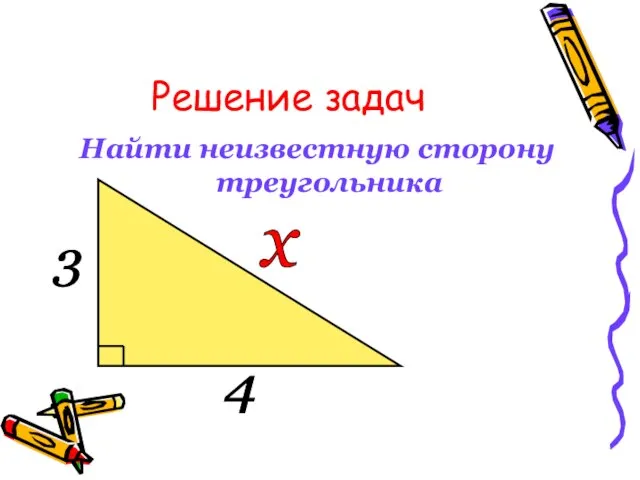
Слайд 7Решение задач
Найти неизвестную сторону треугольника
3
4
х
Слайд 8Определите
Какой треугольник является прямоугольным?
13 м; 5 м; 12 м;
2) 0,6 дм;

0,8 дм; 1,2 дм.
Слайд 9Древнерусская задача
Случися некоему человеку
к стене лествицу прибрати,
стены тоя же высота

есть 117 стоп. И обрете лествицу
долготою 125 стоп. И ведати хощет,
колико стоп сея лествици нижний конец
от стены отстояти имать.
Дано: ? АВС, ? 90º,
АС = 117 стоп,
АВ = 125 стоп.
Найти: ВС
Слайд 10Тополь у реки
«На береге реки рос тополь одинокий.
Вдруг ветра порыв его ствол

надломал.
Бедный тополь упал. И угол прямой
С течением реки его угол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Дано: АС = 3 фута, AD = 4 фута, BC = CD.
Найти: АВ.









 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»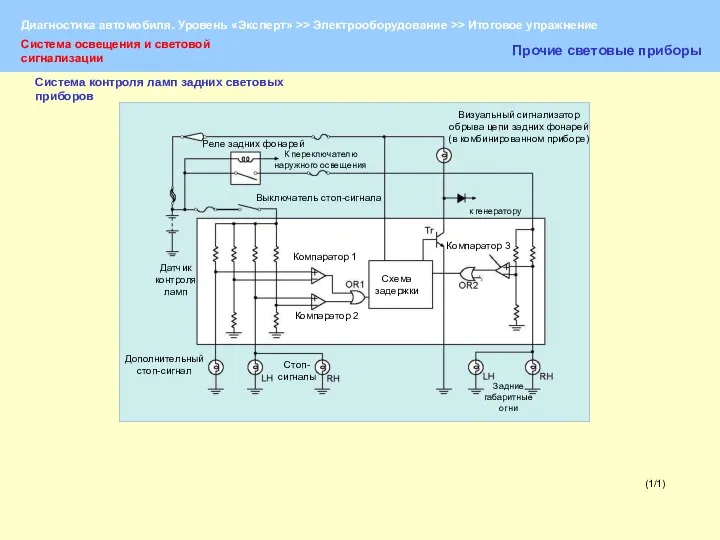 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс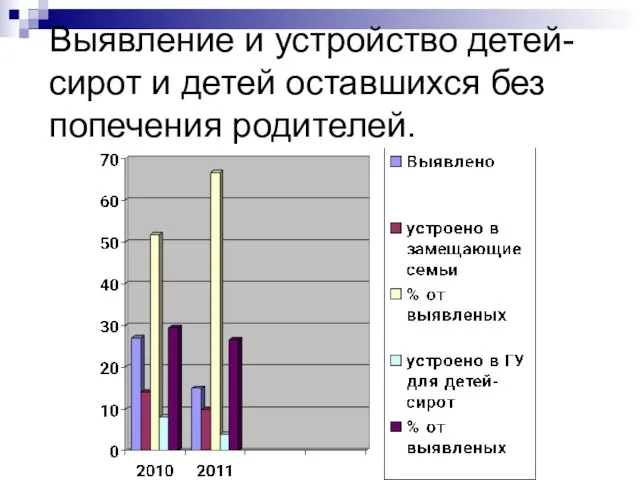 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства