Содержание
- 2. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника? В
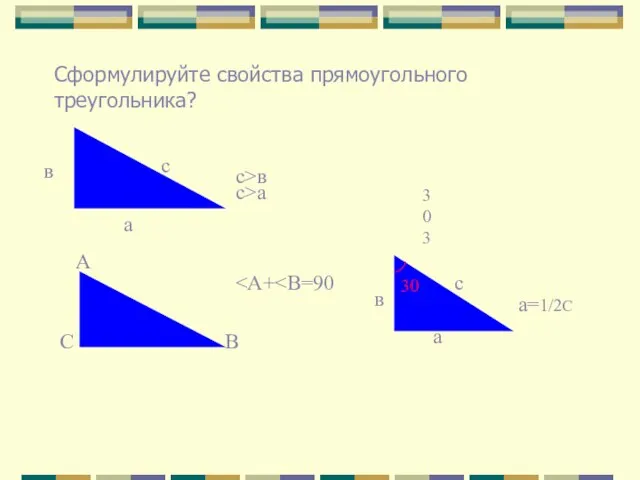
- 3. Сформулируйте свойства прямоугольного треугольника? с а с>в с>а А В С 303 в а с 30
- 4. Сформулируйте признаки равенства прямоугольных треугольников. _ 1 2 3 4
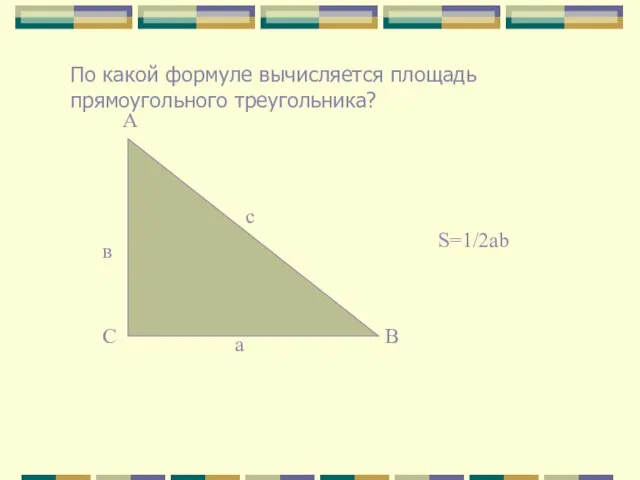
- 5. По какой формуле вычисляется площадь прямоугольного треугольника? с в а А В С S=1/2ab
- 6. Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость которого было доказано древнегреческим философом и
- 7. Формулировка теоремы « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
- 8. Современная формулировка « В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 9. Сказка Много лет тому назад жила – была очень красивая принцесса. Её красоте завидовали многие. В
- 10. Нашелся богатырь, который был готов спасти принцессу. Чтобы угадать секрет колдовства , богатыря отправили к Пифагору.
- 11. Пифагор разъяснил формулу для вычисления расстояния до окна принцессы.
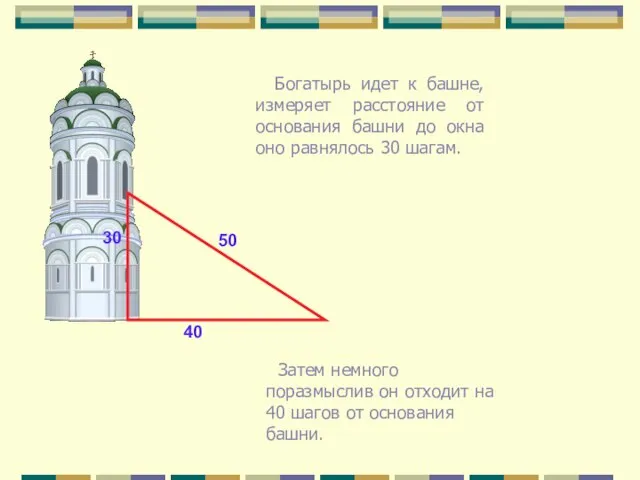
- 12. Богатырь идет к башне, измеряет расстояние от основания башни до окна оно равнялось 30 шагам. 30
- 13. И вдруг перед богатырем появляется прекрасная принцесса.
- 14. ТЕОРЕМА ПИФАГОРА Дано: треугольник ABC, угол С – прямой, АВ=c, ВС=а, АС=b Доказать: с2 = а2
- 15. Достроим квадраты на катетах и гипотенузе треугольника
- 16. Задания 1. Разделите квадраты построенные на катетах на несколько фигур. При делении квадратов отрезки должны быть
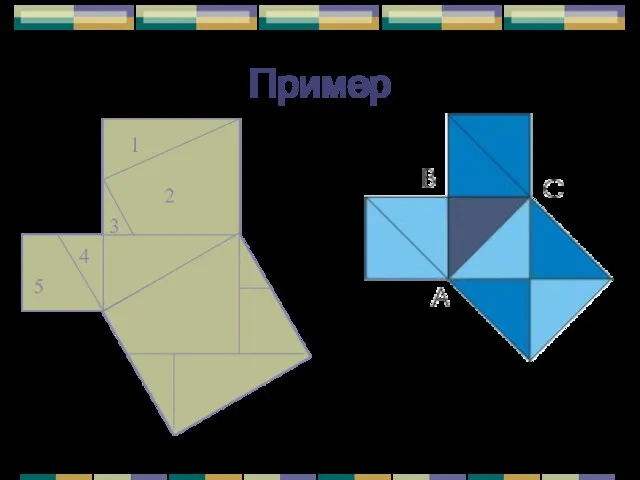
- 17. Пример
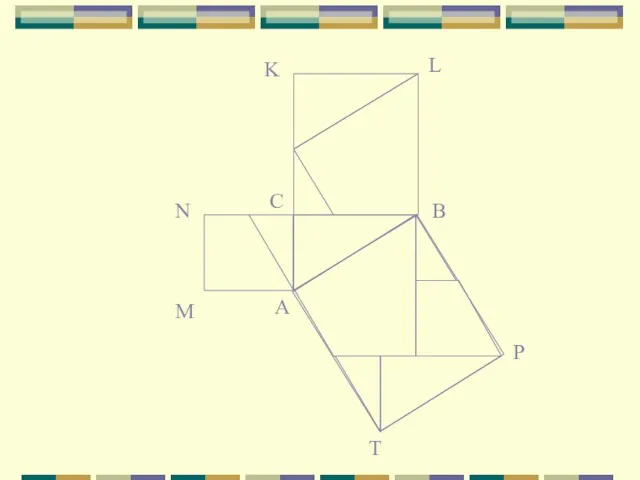
- 18. А С В М N K L P T
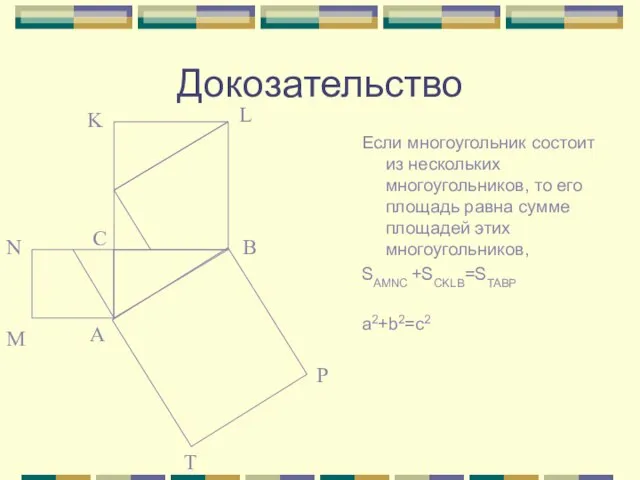
- 19. Докозательство Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, SAMNC
- 20. 2 способ доказательства теоремы
- 21. Доказательство: Треугольник АВС дополняем до квадрата со сторонами равными а + b. Площадь такого квадрата равна
- 22. Рассмотрим и другие варианты доказательства теоремы Пифагора http://th-pif.narod.ru/razlog.htm http://th-pif.narod.ru/pract.htm
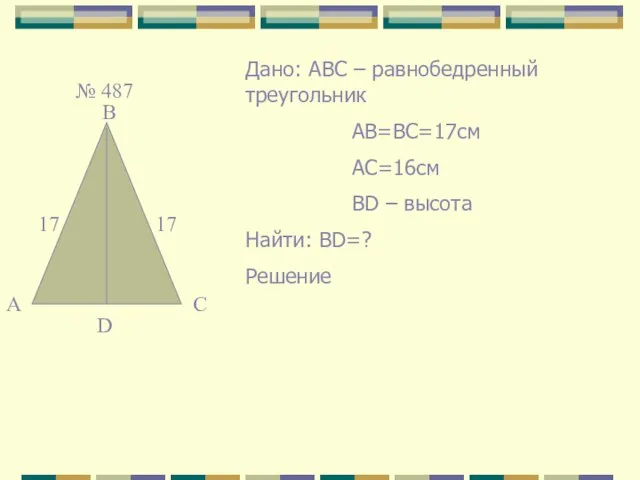
- 23. № 487 А В С 17 17 D Дано: АВС – равнобедренный треугольник АВ=ВС=17см АС=16см ВD
- 25. Скачать презентацию














 Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной
Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной Средства регулирования движением поездов
Средства регулирования движением поездов Афины при Перикле
Афины при Перикле Электронная таблица EXCEL
Электронная таблица EXCEL Архетипы
Архетипы УНИДРУА: международный институт по унификации частного права
УНИДРУА: международный институт по унификации частного права Органы чувств
Органы чувств  «Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения»
«Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения» Новогодние открытки
Новогодние открытки Робототехника. Проект
Робототехника. Проект Балансирующий рынок
Балансирующий рынок Теорема Пифагора
Теорема Пифагора Культура XX века
Культура XX века Деревня Юрьевец
Деревня Юрьевец Wine. The benefits of wine with moderate consumption
Wine. The benefits of wine with moderate consumption Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов
Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов Воздействие высокоскоростных магистралей на окружающую среду
Воздействие высокоскоростных магистралей на окружающую среду Презентация экскурсии в животноводческий комплекс «ИП Каюмов»
Презентация экскурсии в животноводческий комплекс «ИП Каюмов» 07_0___163
07_0___163 каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в
каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в «Белые» в Гражданской войне
«Белые» в Гражданской войне Внедрение здоровьесберегающих технологий
Внедрение здоровьесберегающих технологий Русское искусство 2 пол.19 века
Русское искусство 2 пол.19 века Всегда ли правы мы- родители?
Всегда ли правы мы- родители? Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова
Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова Семейные традиции семьи Митрофановых
Семейные традиции семьи Митрофановых HADI – это экспериментальный научный метод исследования, переложенный на бизнес
HADI – это экспериментальный научный метод исследования, переложенный на бизнес ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс
ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс