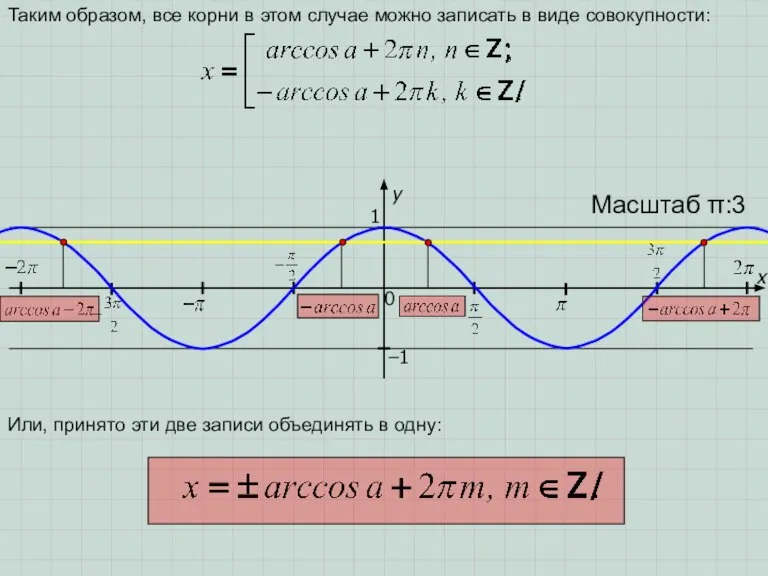
причем их абсциссы определяются следующим образом:
a
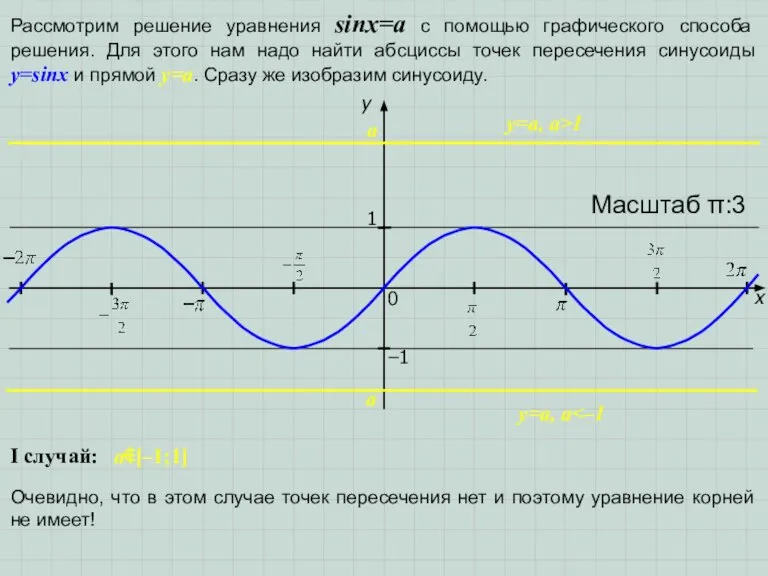
1) Рассмотрим точку, абсцисса которой попадает на отрезок .
2) Абсцисса этой точки – есть число(угол в радианной мере), синус которого равен a, т.е. значение этого числа равно arcsina.
3) Абсцисса второй точки, попадающей на отрезок [–π; π], равна (π–arcsina). Для объяснения этого достаточно вспомнить, что sinx=sin(π–x).
4) Все остальные абсциссы точек пересечения получаются из этих двух добавлением к ним чисел вида 2πn, где n∈ (ведь мы помним свойство периодичности функции y=sinx). Задание: назовите, какие абсциссы «улетевших» за край чертежа двух точек?
Ответ: (arcsina+2π) и (3π – arcsina).

![x y 1 0 Масштаб π:3 −1 II случай: a∈[–1;1] Очевидно, что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338054/slide-3.jpg)
![x y 1 0 Масштаб π:3 −1 II случай: a∈[–1;1] Очевидно, что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338054/slide-7.jpg)
 vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Бином Ньютона
Бином Ньютона Дробно-рациональные уравнения
Дробно-рациональные уравнения Арксинус, арккосинус, арктангенс и арккотангенс
Арксинус, арккосинус, арктангенс и арккотангенс Производная
Производная Урок алгебры в 7 классе Тема: «Разность квадратов»
Урок алгебры в 7 классе Тема: «Разность квадратов»  История развития Олимпийских игр в Древней Греции
История развития Олимпийских игр в Древней Греции  Свойства функции
Свойства функции Алгебра. Теоретический материал
Алгебра. Теоретический материал Степенная функция - презентация по Алгебре_
Степенная функция - презентация по Алгебре_ Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt
Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt Крестовые походы
Крестовые походы Презентация на тему Арбитражные аппеляционные суды
Презентация на тему Арбитражные аппеляционные суды  Презентация на тему Достопримечательности Египта
Презентация на тему Достопримечательности Египта  Обратные тригонометрические функции
Обратные тригонометрические функции Старинные ЗАНИМАТЕЛЬНЫЕ задачи
Старинные ЗАНИМАТЕЛЬНЫЕ задачи Logarifmicheskaya-funkciya.ppt
Logarifmicheskaya-funkciya.ppt Неопределённый интеграл и методы его исчисления
Неопределённый интеграл и методы его исчисления Квадратичная функция (7 класс)
Квадратичная функция (7 класс) Эпоха Просвещения в России
Эпоха Просвещения в России Размах и мода ряда чисел
Размах и мода ряда чисел Презентация на тему Основные теории местного самоуправления
Презентация на тему Основные теории местного самоуправления  Календарь история возникновения
Календарь история возникновения Свойства функций непрерывных на отрезке
Свойства функций непрерывных на отрезке Типы иррациональных уравнений Примеры решения
Типы иррациональных уравнений Примеры решения  Доказательство тождеств
Доказательство тождеств Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Презентация на тему спорт как альтернативу пагубным привычкам»
Презентация на тему спорт как альтернативу пагубным привычкам»