Содержание
- 2. Тема урока « Решение неравенств второй степени с одной переменной»
- 3. План урока Повторение по теме «Квадратичная функция и её свойства» Изучение нового материала по теме «Решение
- 4. Вопросы, необходимые решить на уроке Как связаны понятия квадратичная функция и неравенства второй степени с одной
- 5. Квадратичная функция и её свойства Дайте определение квадратичной функции. У = а Х² + в Х
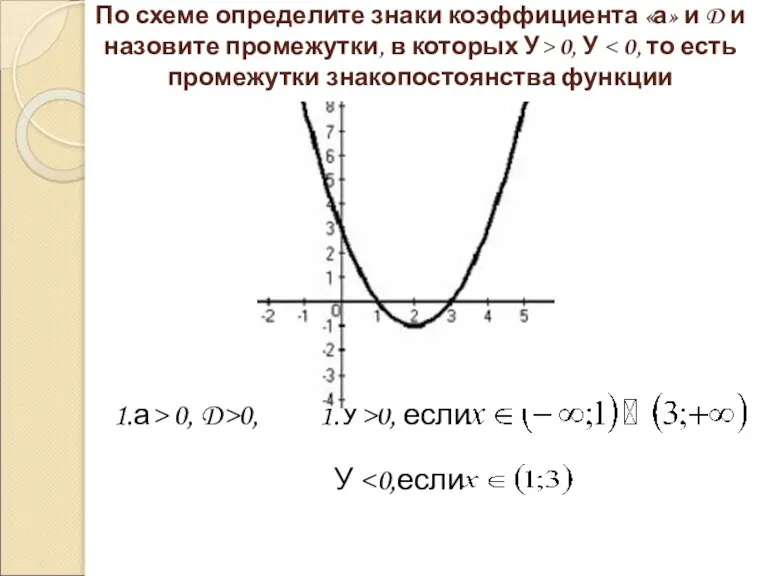
- 6. По схеме определите знаки коэффициента «а» и D и назовите промежутки, в которых У> 0, У
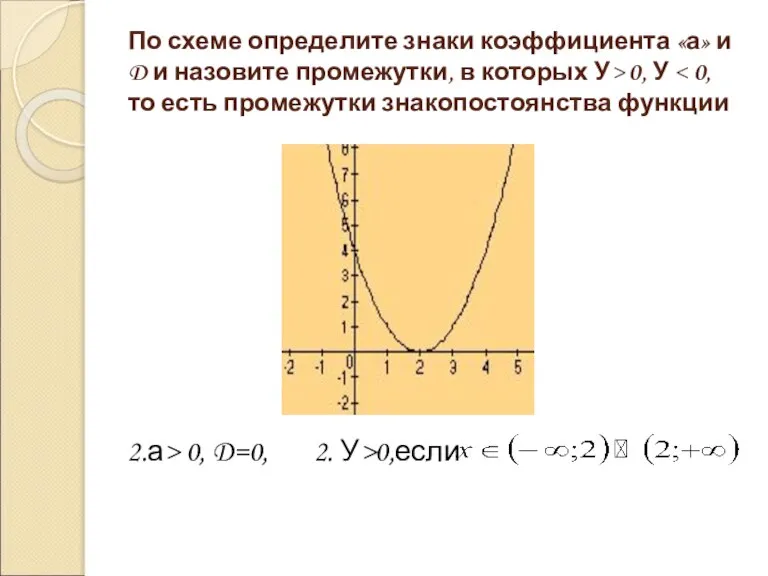
- 7. По схеме определите знаки коэффициента «а» и D и назовите промежутки, в которых У> 0, У
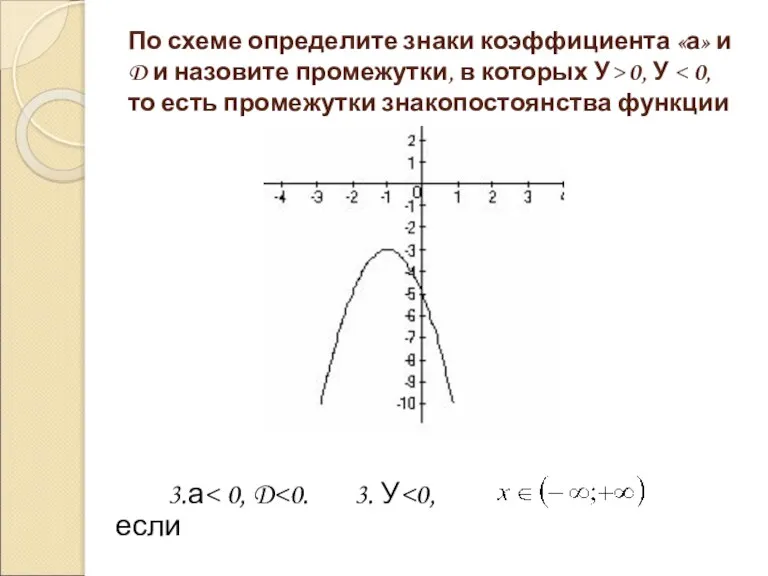
- 8. По схеме определите знаки коэффициента «а» и D и назовите промежутки, в которых У> 0, У
- 9. Решить неравенства -2x²+x+3 0; X²+2x-3 >0 (-∞;-1]U[1,5;+∞) (- ∞;-3)U(-1;+∞)
- 10. Решить неравенство Х² - Х- 30 Какая информация о квадратичной функции может оказаться полезной? знак коэффициента
- 11. Алгоритм решения неравенств второй степени с одной переменной определить знак коэффициента а квадратичной функции У =
- 12. Физминутка
- 13. Используя алгоритм, решите неравенства 1 вариант: Х² + 4Х – 4 0 2 вариант: Х² –
- 14. Квадратные неравенства в окружающем мире Выполнила ученица 9 класса Варыгина Анна, МОУ «СОШ с.Тепляковка Базарнокарабулакского района
- 15. Квадратичные неравенства в окружающем мире
- 16. Каскады падающей воды украшают многие города. А причём здесь квадратные неравенства? Но оказывается есть связь между
- 17. Для любителей экстремальной езды на мотоцикле будет интересно знать, что прыгая через ряды машин, необходимо использовать
- 18. И тут неравенства!
- 19. В окружающем мире
- 20. Квадратные неравенства в окружающем мире
- 22. Скачать презентацию




![Решить неравенства -2x²+x+3 0; X²+2x-3 >0 (-∞;-1]U[1,5;+∞) (- ∞;-3)U(-1;+∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338050/slide-8.jpg)











 Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Формулы приведения
Формулы приведения Интегралы
Интегралы Алгебраические дроби
Алгебраические дроби  Линейные уравнения ax=b
Линейные уравнения ax=b Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Эпоха Просвещения в России
Эпоха Просвещения в России Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Таблицы истинности
Таблицы истинности Теорема Виета (8 класс)
Теорема Виета (8 класс) Preobrazovanie-dvoynyh-radikalov.ppt
Preobrazovanie-dvoynyh-radikalov.ppt Решение заданий В9
Решение заданий В9 Алгебра и начала анализа
Алгебра и начала анализа Интеграл
Интеграл Свойства степени
Свойства степени Презентация на тему Как связаны неживая и живая природа
Презентация на тему Как связаны неживая и живая природа  Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Линейное уравнение с одним неизвестным
Линейное уравнение с одним неизвестным Тема: «Одночлены»
Тема: «Одночлены» Презентация на тему Таможня в 21-ом веке
Презентация на тему Таможня в 21-ом веке Классная работа. Пропорции. 11.01.13
Классная работа. Пропорции. 11.01.13 Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Квадратные уравнения
Квадратные уравнения Применение неравенств и их свойств
Применение неравенств и их свойств Свойства корня n-ой степени
Свойства корня n-ой степени Формула корней квадратного уравнения
Формула корней квадратного уравнения Metod-racionalizacii.pptx
Metod-racionalizacii.pptx Презентация на тему Виды и особенности экологических правоотношений
Презентация на тему Виды и особенности экологических правоотношений