Решение систем линейных уравнений (7 класс)

Общеобразовательное учебное заведение
ПМГ математики
Россия, Тольятти
445057, Приморский б-р, 25
Тел. [phone]
Факс [phone]
Тольяттинская
Академия
Управления

Алгебра стоит на четырёх китах
Число
Уравнение
Тождество
Функция

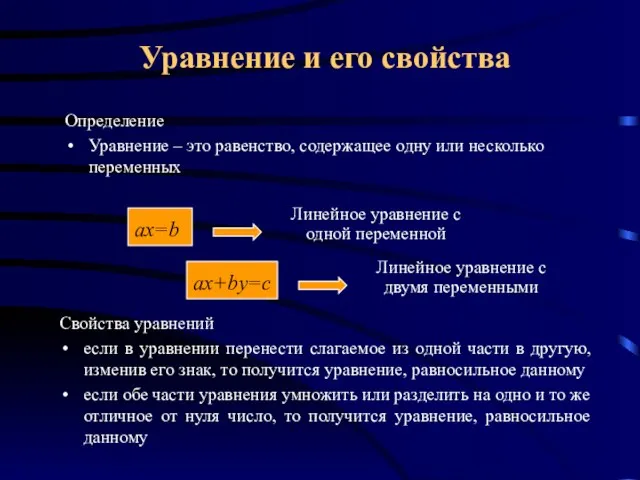
Определение
Уравнение – это равенство, содержащее одну или несколько переменных
Линейное уравнение с
одной переменной
Линейное уравнение с
двумя переменными
Свойства уравнений
если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному
Уравнение и его свойства

Система уравнений и её решение
Определения
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет

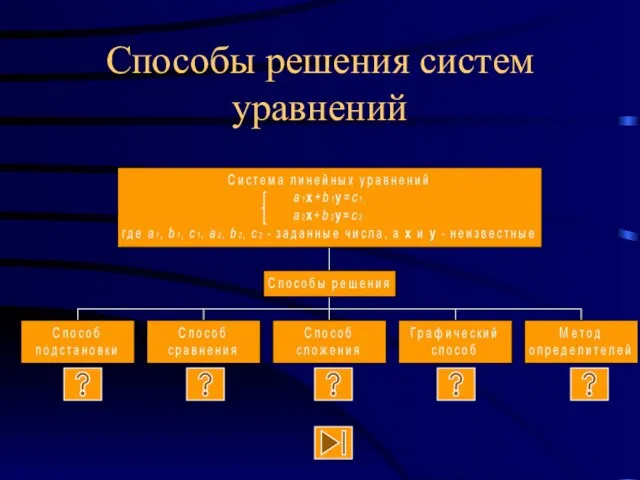
Способы решения систем уравнений

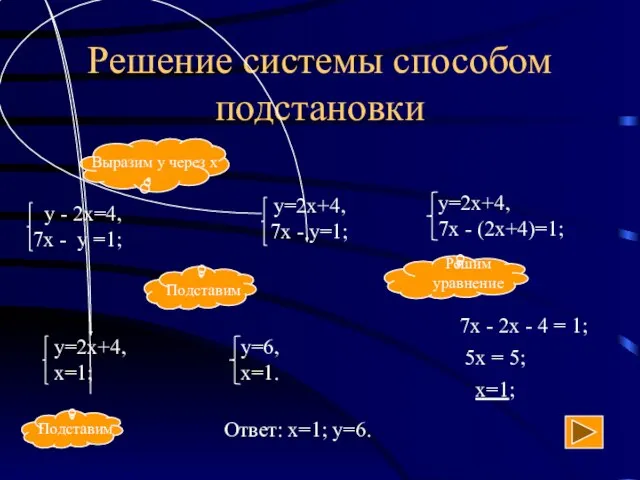
Решение системы способом подстановки
7х - 2х - 4 = 1;
5х = 5;
х=1;
Ответ: х=1; у=6.

Способ подстановки (алгоритм)
Из какого-либо уравнения выразить одну переменную через другую
Подставить полученное выражение для переменной в другое уравнение и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .

Решение системы способом сравнения
Приравняем
выражения
для у
7х - 1=2х+4,
7х - 2х=4+1,
5х=5,
х=1.
Решим
уравнение
Ответ: (1; 6)

Способ сравнения (алгоритм)
Выразить у через х (или х через у) в каждом уравнении
Приравнять выражения, полученные для одноимённых переменных
Решить полученное уравнение и найти значение одной переменной
Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
Записать ответ: х=…; у=… .

Решение системы способом сложения
||·(-3)
+
____________
Ответ: (3; - 10)

Способ сложения (алгоритм)
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .

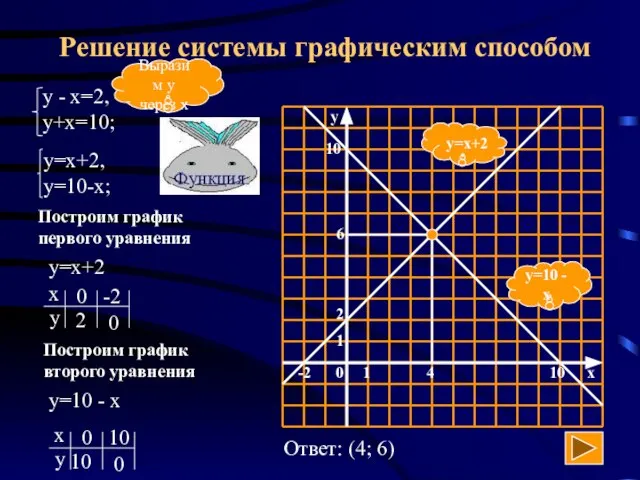
Решение системы графическим способом
y=10 - x
y=x+2
Выразим у
через х
Построим график
первого уравнения
у=х+2
Построим график
второго уравнения
у=10 - х
Ответ: (4; 6)

Графический способ (алгоритм)
Выразить у через х в каждом уравнении
Построить в одной системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)

-80
Решение системы методом определителей
Составим матрицу из коэффициентов
при неизвестных Δ
= 7·6 - 2·17 = 42 - 34 = 8
= 1·6 - 2·(-9) = 6 + 18 = 24
= 7·(-9) - 1·17 = - 63 -17= -80
Составим определи-
тель Δx, заменив в определи-
теле Δ первый столбец
на столбец свободных
членов
Составим определи-
тель Δy, заменив в определи-
теле Δ второй столбец
на столбец свободных
членов
Δx
х=
Δ
=
24
8
=
3;
у=
Δy
Δ
=
8
= -10.
Найдем
х и у
Ответ: х=3; у= -10.

Метод определителей (алгоритм)
Составить табличку (матрицу) коэффициентов при неизвестных и вычислить определитель Δ.
Найти - определитель Δx, получаемый из Δ заменой первого столбца на столбец свободных членов.
Найти - определитель Δy, получаемый из Δ заменой второго столбца на столбец свободных членов.
Найти значение переменной х по формуле Δx / Δ.
Найти значение переменной у по формуле Δy / Δ.
Записать ответ: х=…; у=… .