Формула корней квадратного уравнения

Вы хотите научиться решать квадратные уравнения?
ДА
НЕТ

Вы хотите научиться решать квадратные уравнения?
ДА
НЕТ

Вы хотите научиться решать квадратные уравнения?
ДА
НЕТ

Содержание
Определение квадратного уравнения
Дискриминант квадратного уравнения
Формула корней квадратного уравнения
Задачи
Полезный материал
Тест
Самостоятельная работа

Определение квадратного уравнения.
Опр. 1. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где х –переменная, а, b и с - некоторые числа, причем а ≠ 0.
Числа а, b и с - коэффициенты квадратного уравнения. Число а называют первым коэффициентом, b – вторым коэффициентом и с – свободным членом.

Дискриминант квадратного уравнения
Опр. 2. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac.
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D > 0
D = 0
D < 0

Если D > 0
В этом случае уравнение ах2 + bх + с = 0 имеет два действительных корня:

Если D = 0
В этом случае уравнение ах2 + bх + с = 0
имеет один действительный корень:

Если D < 0
Уравнение ах2 + bх + с = 0 не имеет действительных корней.

Формула корней квадратного уравнения
Обобщив рассмотренные случаи получаем
формулу корней квадратного уравнения
ах2 + bх + с = 0.
К тесту

Задачи
Решить уравнение 2x2- 5x + 2 = 0.
Решить уравнение 2x2- 3x + 5 = 0.
Решить уравнение x2- 2x + 1 = 0.

Решить уравнение 2x2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 4⋅2⋅2 = 9.
Так как D > 0, то уравнение имеет два корня.
Найдем их по формуле
то есть x1 = 2 и x2 = 0,5 - корни заданного уравнения.
К задачам

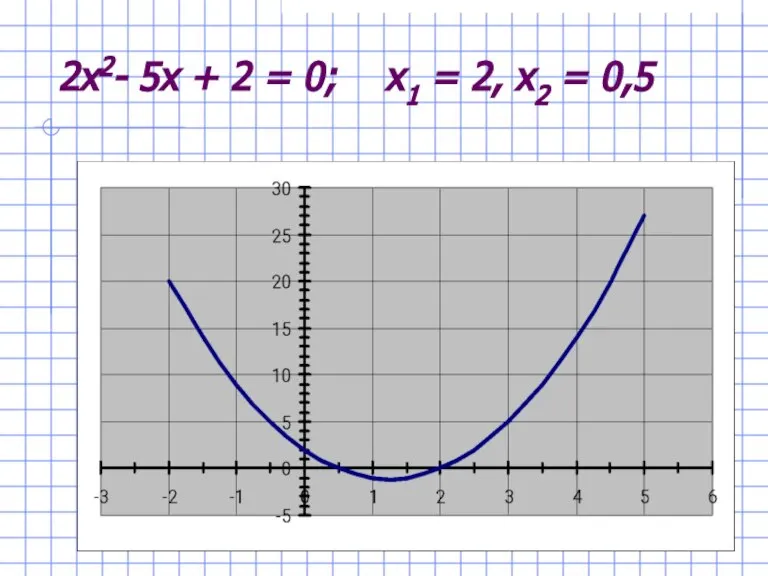
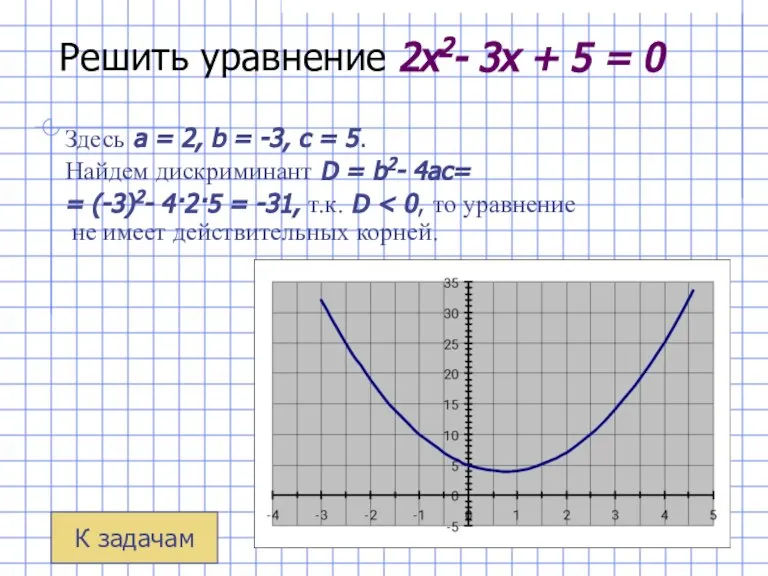
2x2- 5x + 2 = 0; x1 = 2, x2 = 0,5

Решить уравнение 2x2- 3x + 5 = 0
Здесь a = 2, b = -3, c = 5.
Найдем дискриминант D = b2- 4ac=
= (-3)2- 4·2·5 = -31, т.к. D < 0, то уравнение
не имеет действительных корней.
К задачам

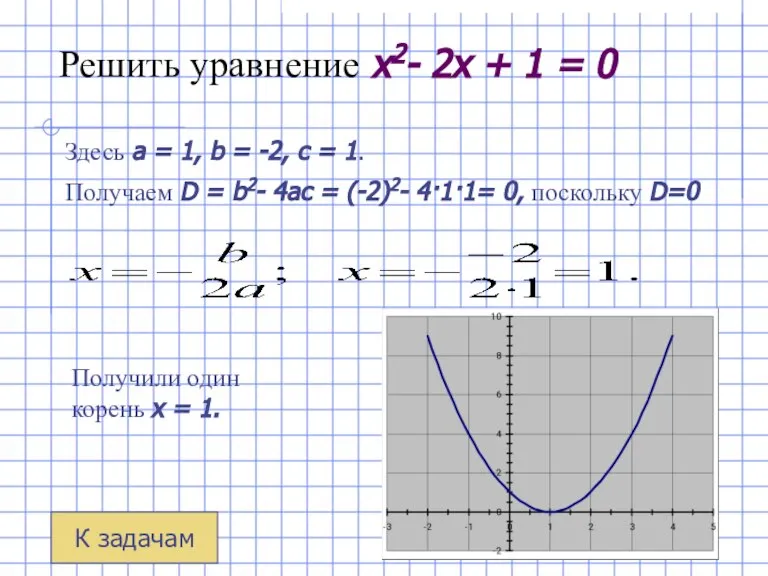
Решить уравнение x2- 2x + 1 = 0
Здесь a = 1, b = -2, c = 1.
Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0
Получили один корень х = 1.
К задачам

Полезный материал
Определение квадратного уравнения
Определение приведенного квадратного уравнения
Определение дискриминанта
Формула корней квадратного уравнения
Коэффициенты квадратного уравнения

Определение приведенного квадратного уравнения
Опр. 3. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1.
х2 + bх + с = 0

Тест
1. Вычислите дискриминант уравнения х2-5х-6=0.
0
-6
1
25
-5
49
Следующий вопрос

2. Сколько корней имеет уравнение, если D < 0?
Три корня
Один корень
Два корня
Корней не имеет
Следующий вопрос

3. Выберите корни уравнения 2у2-9у+10=0.
у1=-2; у2=-2,5
Корней не имеет
у1=2; у2=-2,5
у1=2; у2=2,5

Самостоятельная работа
Вариант 1.
№1. Решите уравнения:
а) х2+7х-44=0;
б) 9у2+6у+1=0;
в) –2t2+8t+2=0;
г) а+3а2= -11.
№2. При каких
значениях х равны значения многочленов:
(2-х)(2х+1) и (х-2)(х+2)?
Вариант 2.
№1. Решите уравнения:
а) х2-10х-39=0;
б) 4у2-4у+1=0;
в) –3t2-12t+6=0;
г) 4а2+5= а.
№2. При каких
значениях х равны значения многочленов:
(1-3х)(х+1) и (х-1)(х+1)?

Молодец !