Содержание
- 2. Математики о производной. « Слова «производная» и «произошло» имеют похожие части слова, да и смысл похож:
- 3. Что называется производной? Производной функции в данной точке называется предел отношения приращения функции в этой точке
- 4. «Алгоритм нахождения производной»
- 5. Исследуя функции, можно встретить случаи, когда функция определена, но не дифференцируема. Что это? Почему так происходит?
- 6. Взгляд из детства. Всем с детства известно такое явление, как движение мяча, падающего на пол и
- 7. При отскоке от пола (при h=0) направление движения мяча меняется (и функция достигает минимума), однако в
- 8. Примеры функций, имеющих особые точки. Все функции вида у = |f(x)|, при f(x)=0 имеют особые точки
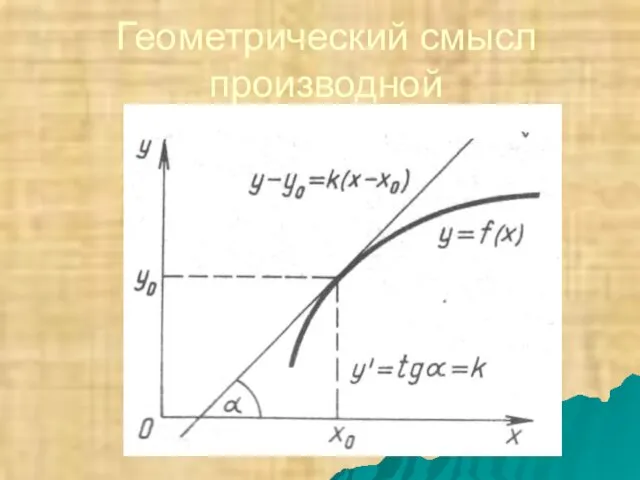
- 9. Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке x равно угловому
- 10. Геометрический смысл производной
- 11. Физический смысл скорость ускорение Производная от перемещения по времени является мгновенная скорость. Производная от скорости по
- 12. Точка движется прямолинейно по закону Вычислите скорость движения точки: а) в момент времени t; б) в
- 13. Найдите скорость и ускорение для точки, движущейся по закону а) в момент времени t; б) в
- 14. Проблемная задача Две материальные точки движутся прямолинейно по законам В какой момент времени скорости их равны,
- 15. Решение проблемной задачи
- 16. Разбор некоторых задач самостоятельной работы m(l) = 3l2 + 5l (г), lАВ = 20 см, ρсер=
- 18. Скачать презентацию














 Презентация на тему Место муниципального права в российском праве
Презентация на тему Место муниципального права в российском праве  Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3
Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3 Командировка в страну квадратных уравнений
Командировка в страну квадратных уравнений ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук
ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук  Действительные числа
Действительные числа Презентация на тему Понятие предпринимательского права
Презентация на тему Понятие предпринимательского права  Квадратичная функция. Её свойства и график 8 класс
Квадратичная функция. Её свойства и график 8 класс Свойства функции 9 класс - презентация_
Свойства функции 9 класс - презентация_ Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766
Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766 Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре Презентация на тему ТЕСТ «Логистика
Презентация на тему ТЕСТ «Логистика  Понятие корня n – й степени из действительного числа
Понятие корня n – й степени из действительного числа «Применение производной для исследования функции»
«Применение производной для исследования функции»  Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_
Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_ Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Статистические характеристики Среднее арифметическое ряда Размах ряда Мода ряда Медиана ряда
Статистические характеристики Среднее арифметическое ряда Размах ряда Мода ряда Медиана ряда  Презентация на тему Никола Тесла - человек из будущего
Презентация на тему Никола Тесла - человек из будущего  Решение систем уравнений второй степени с двумя переменными - презентация по Алгебре_
Решение систем уравнений второй степени с двумя переменными - презентация по Алгебре_ Свойства степени
Свойства степени Степенная функция - презентация по Алгебре_
Степенная функция - презентация по Алгебре_ Презентация на тему Константин Васильев (Великоросс)
Презентация на тему Константин Васильев (Великоросс)  Жанры в музыке
Жанры в музыке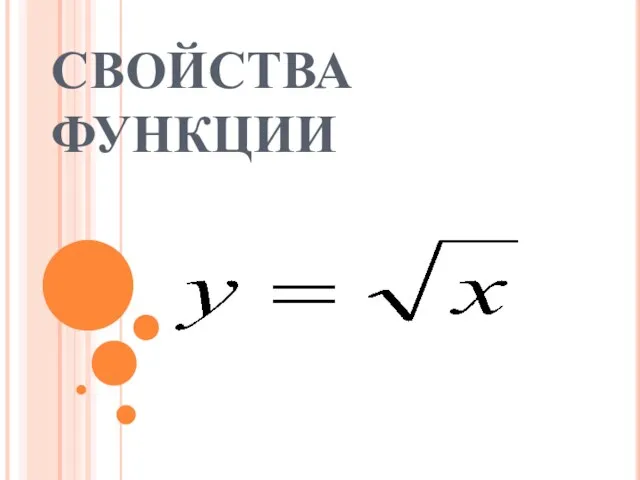 Свойства функции
Свойства функции Презентация на тему Позиции критиков норманской теории
Презентация на тему Позиции критиков норманской теории  Презентация на тему Цели и задачи прокурорского надзора
Презентация на тему Цели и задачи прокурорского надзора  Базовые принципы системы smart-образования
Базовые принципы системы smart-образования Преобразование двойных радикалов 8 класс
Преобразование двойных радикалов 8 класс neravenstva-s-dvumya-peremennymi.ppt
neravenstva-s-dvumya-peremennymi.ppt