Графический метод решения систем уравнений с двумя переменными

Обобщить графический способ решения систем уравнений;
Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные учащимся графики;
Дать наглядные представления, что система двух уравнений с двумя переменными второй степени может иметь от одного до четырех решений, или не иметь решений.
Цели:

Элементарные функции и их графики:
Линейная функция: y=kx+b,
график – прямая.
Прямая пропорциональность: y=kx,
график – прямая, проходящая через начало координат.
Постоянная функция: y=b,
график – прямая, проходящая через точку с координатами
(0;b), параллельно оси абсцисс.
Обратная пропорциональность: y=k/x,
график – гипербола.
Квадратичная функция: y=ax2+bx+c,
график – парабола.
Функция вида: y=x3,
график – кубическая парабола.
Функция вида: y=√x,
график – «ветвь» параболы, расположенная в I четверти.
Уравнение с двумя переменными:
Уравнение окружности: (x - xo)2+(y - yo)2=R2,
график – окружность с центром в точке (xo; yo) и
радиусом R.

Устная работа:
Выразите переменную у через переменную х и
определите, что представляет собой график
уравнения:

Устная работа:
2. Определите координаты центра и радиуса
окружности:

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Графическое решение системы уравнений с двумя переменными сводится к отысканию координат общих точек графиков уравнений.
Этапы решения:
Постройте графики каждого уравнения системы в
координатной плоскости.
Найдите координаты общих точек этих графиков.
Запишите ответ.
Замечание. Графический способ позволяет решить систему лишь приближенно, поэтому для получения точного ответа полученные решения следует проверить подстановкой в условие, или выбрать другой способ решения.

1. x+y=2  y=2–x - линейная
функция, график – прямая;
Решите графически систему уравнений:
A(0;2)
B(2;0)
Ответ: (0;2), (0;2).
2. x2+y2=4 – уравнение
окружности, с центром в (0;0) и R=2;
3. А(0;2) и В(2;0) – точки
пересечения графиков.

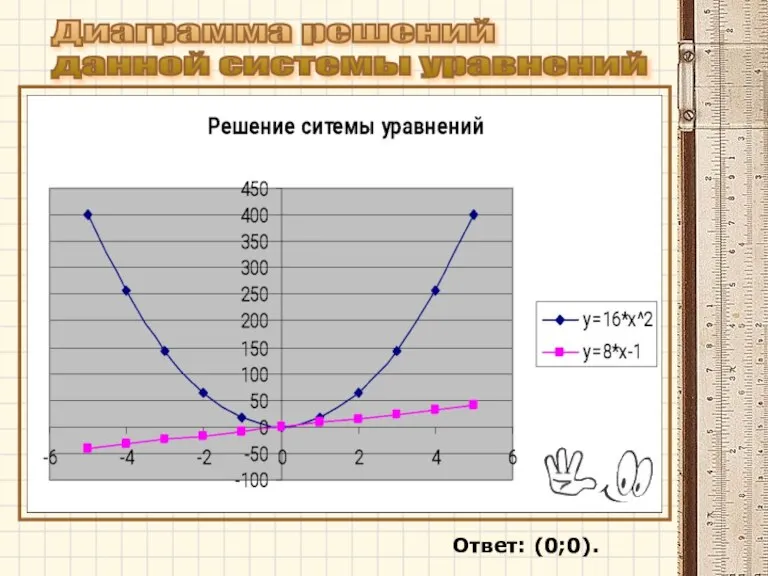
Применение табличного процессора Exel для графического решения уравнений n-й степени.
Рассмотрим решение
следующей системы уравнений:

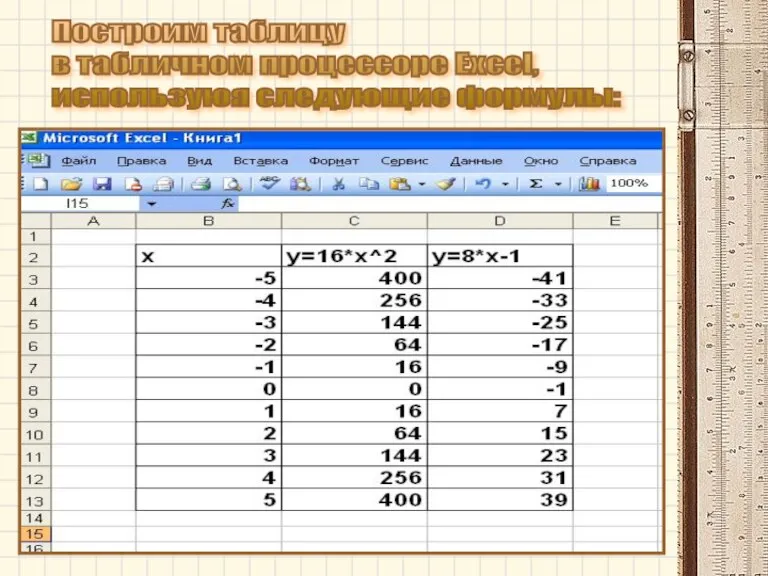
Построим таблицу
в табличном процессоре Excel,
используюя следующие формулы:

Ответ: (0;0).
Диаграмма решений
данной системы уравнений

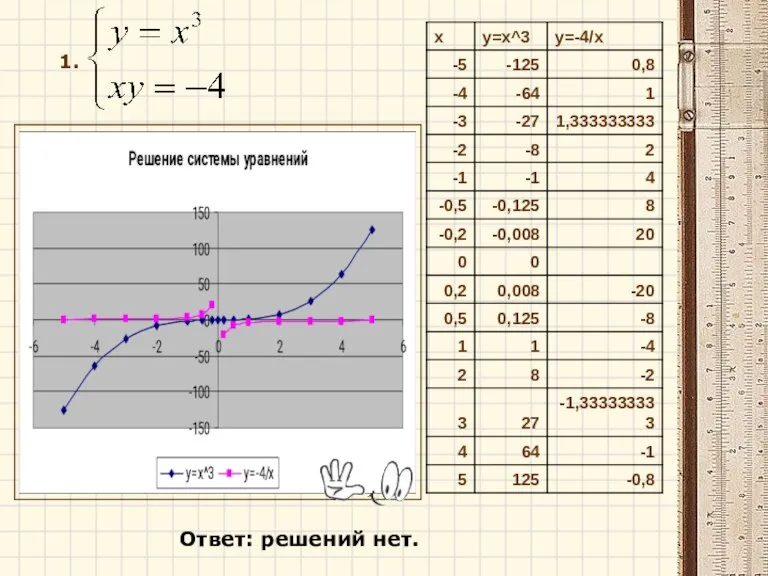
Решить системы уравнений в табличном процессоре Excel:
1.
2.
3.

1.
Ответ: решений нет.

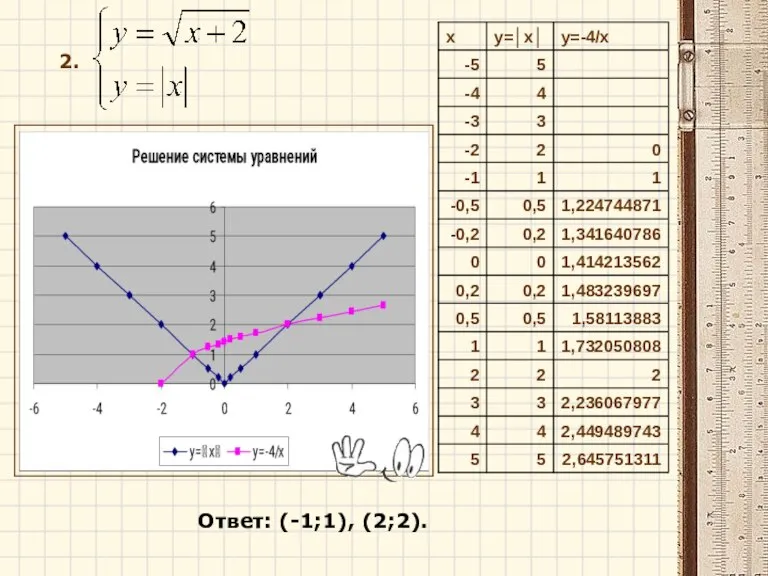
2.
Ответ: (-1;1), (2;2).

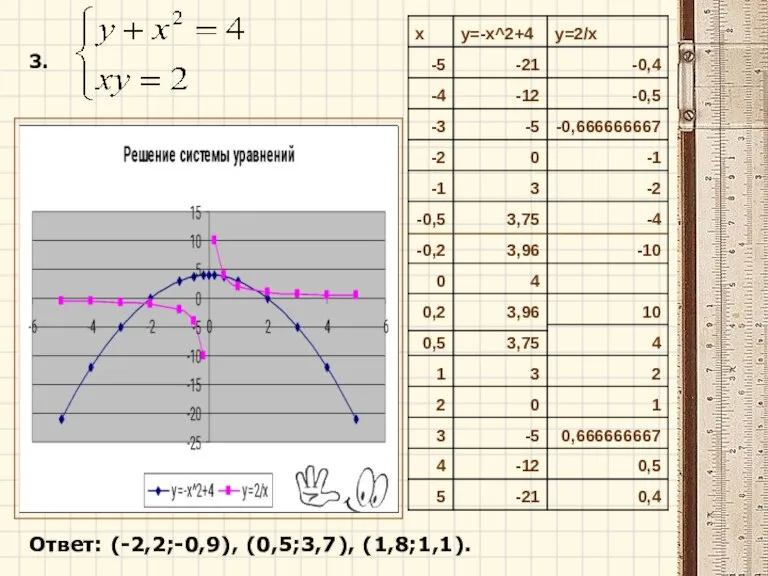
3.
Ответ: (-2,2;-0,9), (0,5;3,7), (1,8;1,1).