Содержание
- 2. ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Комплексные числа. Геометрическая интерпретация комплексных чисел.
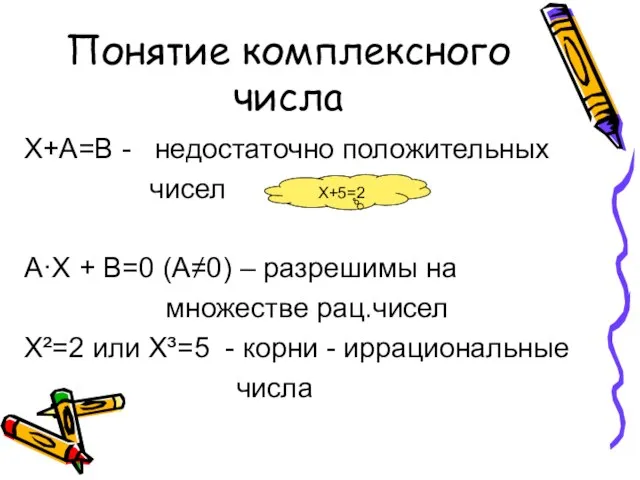
- 3. Понятие комплексного числа Х+А=В - недостаточно положительных чисел А·Х + В=0 (А≠0) – разрешимы на множестве
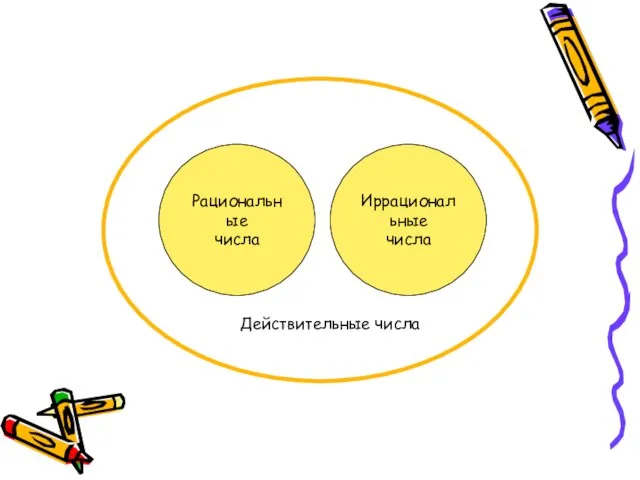
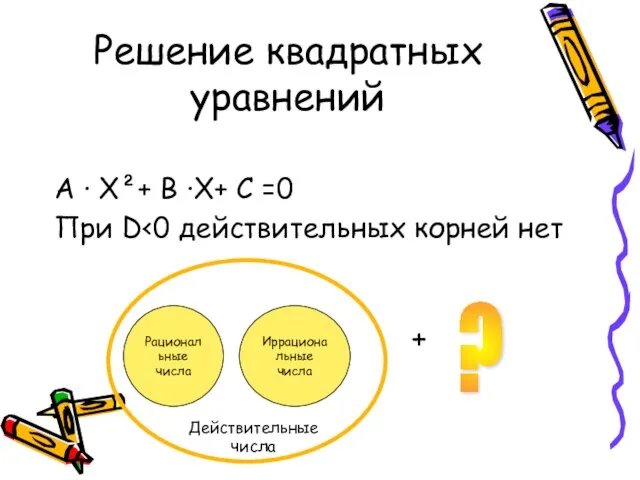
- 5. Решение квадратных уравнений А · Х²+ В ·Х+ С =0 При D
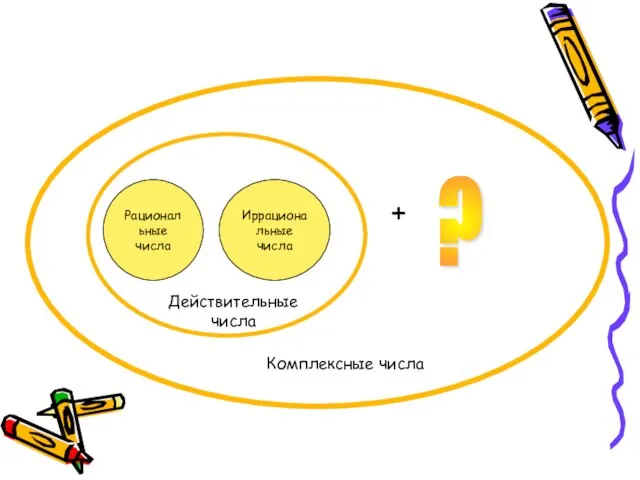
- 6. Комплексные числа
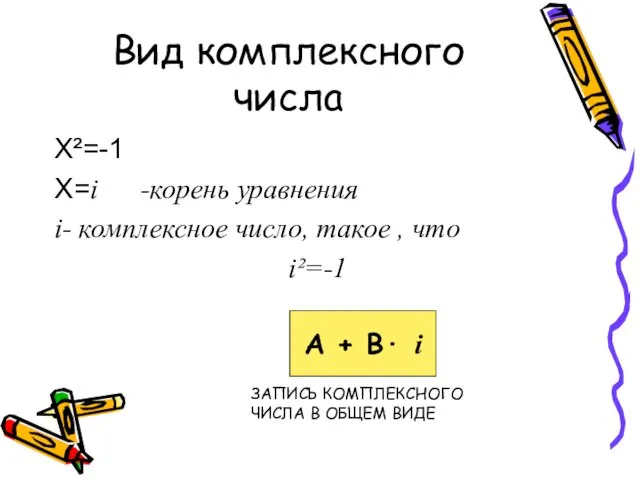
- 7. Вид комплексного числа Х²=-1 Х=i -корень уравнения i- комплексное число, такое , что i²=-1 А +
- 8. А и В – действительные числа i- некоторый символ , такой, что i²= -1 А –
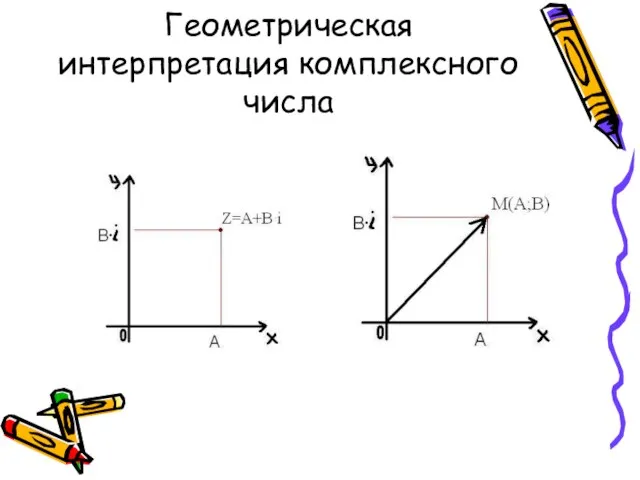
- 9. Геометрическая интерпретация комплексного числа
- 10. Модуль комплексного числа Z=А - В· i СОПРЯЖЕННОЕ Z= А + В· i (Z) = Z
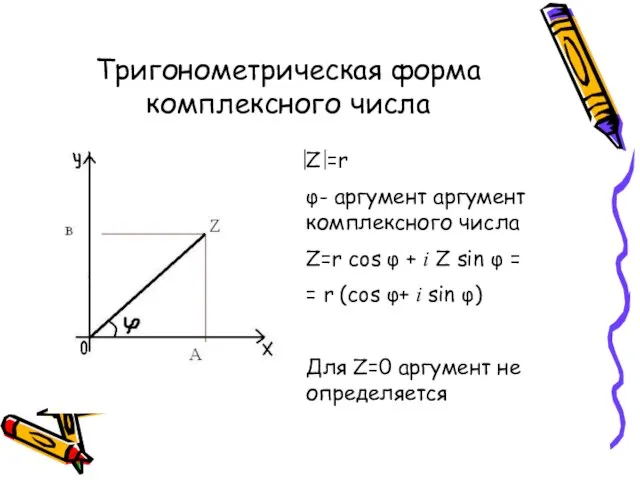
- 11. Тригонометрическая форма комплексного числа Z =r φ- аргумент аргумент комплексного числа Z=r cos φ + i
- 12. Т.к Z =r = Z= А + В· i= cosφ+i sinφ
- 13. Сложение и умножение комплексных чисел Алгебраическая форма Геометрическая форма Сумма (A+iB) + (C+iD)= (A+C)+(B+D)I Произведение Z1=
- 14. Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² (cos2 φ+ i
- 15. Число Z называется корнем степени n из числа ω (обозначается ), если (*) Из данного определения
- 16. Вторая формула Муавра определяет все корни двучленного уравнения степени n Каждое алгебраическое уравнение степени n имеет
- 17. Пример: Решить уравнение:
- 18. Свойства сложения и умножения Переместительное свойство: Сочетательное свойство: Распределительные свойство: Z1 + Z2 = Z1 +Z2
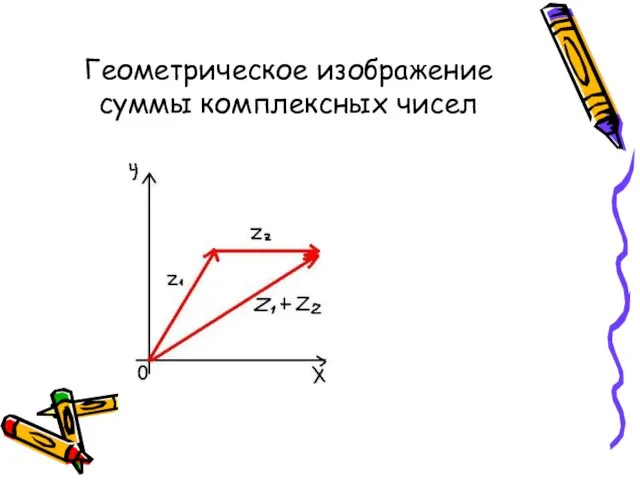
- 19. Геометрическое изображение суммы комплексных чисел
- 20. Вычитание и деление комплексных чисел Z+ Z2 = Z1 Вычитание – операция, обратная сложению: Z+ Z2
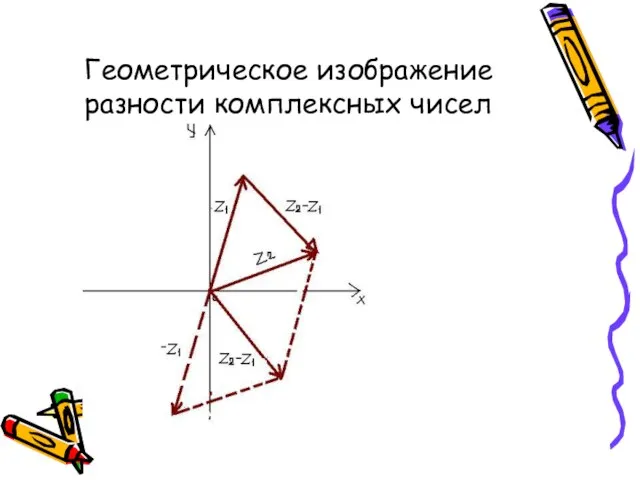
- 21. Геометрическое изображение разности комплексных чисел
- 22. Примеры: Найти разность и частное комплексных чисел Решение:
- 24. Скачать презентацию


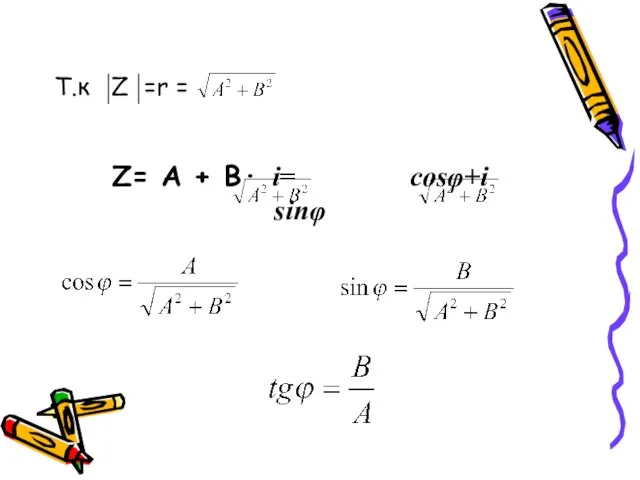

![Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²=](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/266062/slide-13.jpg)






 Презентация на тему Даниил Заточник
Презентация на тему Даниил Заточник Pervoobraznaya.ppt
Pervoobraznaya.ppt Методы решения квадратного уравнения
Методы решения квадратного уравнения Действия над обыкновенными дробями
Действия над обыкновенными дробями Применение неравенств и их свойств
Применение неравенств и их свойств Дробные рациональные уравнения
Дробные рациональные уравнения Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Прогрессия - движение вперёд !
Прогрессия - движение вперёд ! Неравенства и их решения
Неравенства и их решения  Элементы математической статистики
Элементы математической статистики Презентация на тему Основные закономерности развития науки
Презентация на тему Основные закономерности развития науки  Презентация на тему ДЖОРДАНО БРУНО
Презентация на тему ДЖОРДАНО БРУНО  Алгебра модуля
Алгебра модуля Приём вычислений вида 26+4 Математика 2 класс
Приём вычислений вида 26+4 Математика 2 класс 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Применение производной к исследованию функции
Применение производной к исследованию функции Приращение аргумента. Приращение функции
Приращение аргумента. Приращение функции Неравенства с двумя переменными
Неравенства с двумя переменными Презентация на тему Место муниципального права в российском праве
Презентация на тему Место муниципального права в российском праве  Многочлены
Многочлены Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»
Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»  Эпоха Просвещения в России
Эпоха Просвещения в России Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Понятие обратной функции. Определение логарифмической функции
Понятие обратной функции. Определение логарифмической функции Пропорция
Пропорция Определение производной функции y=f(x) в точке
Определение производной функции y=f(x) в точке Презентация на тему Позиции критиков норманской теории
Презентация на тему Позиции критиков норманской теории