Касательная к графику функции

Содержание
1. Определение касательной к графику функции.
2. Уравнение касательной к графику функции в общем виде.
3. Алгоритм составления касательной к графику функции.
4. Условия параллельности и перпендикулярности двух прямых.
5. Касательная проходит через точку, лежащую на данной прямой.
6. Касательная проходит через точку, не лежащую на данной прямой.
7. Касательная проходит под некоторым углом к данной прямой.
8. Касательная является общей для двух кривых.
9. Является ли данная прямая касательной к графику функции у=f(x)?

Определение касательной к графику функции у=f(х)
Пусть дана некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р1 и проведем прямую через точки Р и Р1. Эту прямую называют секущей. Будем приближать точку Р1 к Р. Положение секущей РР1 будет меняться (стремиться к точки Р) предельное положение прямой РР1 и будет касательной к кривой в точке Р.

Уравнение вида у=f(a)+f’(a)(х-а) является уравнением касательной к графику функции.

Алгоритм составления касательной к графику функции у=f(x)
Обозначить буквой а абсциссу точки касания.
Найти f(а).
Найти f’(x) и f’(а).
Подставить найденные числа а, f(а), f’(а) в общее уравнение касательной у=f(a)+f’(a)(x-a)

Условия параллельности и перпендикулярности двух прямых.
Пусть даны две прямые: у1=k1x+b1 и у2=k2x+b2.
Если k1= k2, то прямая у1 параллельна у2.
Если k1⋅k2=–1, то данные прямые взаимно перпендикулярны

Рассмотрим возможные типы задач на касательную

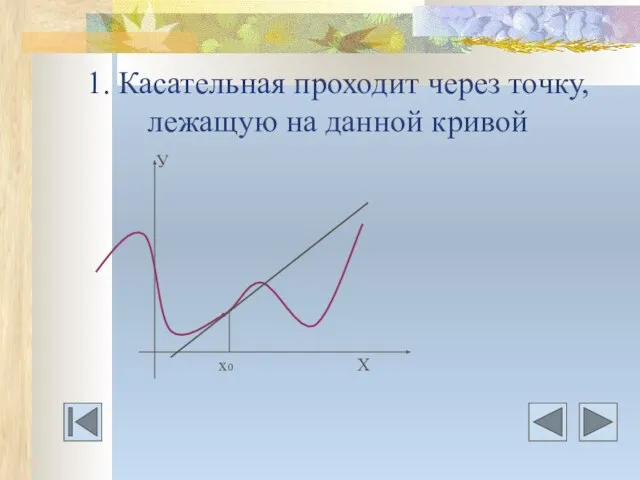
1. Касательная проходит через точку, лежащую на данной кривой
У
.
х0 Х

Даны дифференцируемая функция у=f(х) и
1) абсцисса точки касания;
2) ордината точки касания;
3) абсцисса точки касания задана как пересечение двух графиков функций;
4) абсцисса точки касания задана как корень данного уравнения.

Решение таких задач сводится:
к последовательному отысканию f(a) и f’(a);
решая уравнение f(a)=у0, находим а;
находим точки пересечения двух графиков; решая уравнение f(x)=g(x);
находим корень данного уравнения.

Ключевая задача 1. Составьте уравнение касательной к графику функции у=х2–2х–3 в точке с абсциссой х0=2.
Решение. 1. Обозначим абсциссу точки касания а, тогда а=2.
2. Найдем f(a): f(a)=22–2·2–3, f(a)=-3.
3. Найдем f’ (x) и f’(a): f’(x)=2x–2, f’(a)=2.
4. Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x–a): у=-3+2(х–2),
у=-3+2х–4, у=2х–7 – уравнение касательной.
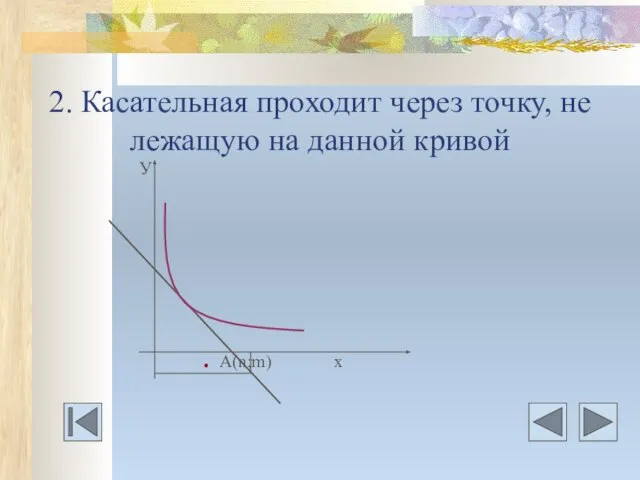
Ответ: у=2х –7.

2. Касательная проходит через точку, не лежащую на данной кривой
У
. A(n;m) х

Даны дифференцируемая функция у=f(х) и
1) точка А(n;m) через которую проходит касательная;
2) точка А(n;m) задана как пересечение двух графиков функций;
3) точка А(n;m) задана как корень системы уравнений.

Решение таких задач основывается на том, что координаты точки А(n;m) должны удовлетворять искомому уравнению касательной:
решая уравнение m=f(a)+f’(a)(m-a) найдем а и, таким образом, приходим к задаче первого типа;
находим точки пересечения двух графиков, решая уравнения f(x)=g(x) и у=g(х) или у=f(x);
находим корень данной системы уравнений.

Ключевая задача 2. Напишите уравнение всех касательных к графику функции
у = х2 +4х+6 проходящих через точку М(-3;-1).
Решение. 1. Точка М(-3;-1) не является точкой касания, так как f(-3)=3.
2. а – абсцисса точки касания.
3. Найдем f(a): f(a) = a 2+4a+6.
4. Найдем f’(x) и f’(a): f’(x)=2x+4, f’(a)=2a+4.
5. Подставим числа а, f(a), в общее уравнение касательной
у= f(a)+ f’(a)(x–a): y=a2+4a+6+(2a+4)(x–a) – уравнение касательной.
Так как касательная проходит через точку М(-3;-1), то -1=a2+4a+6+(2a+4)(-3–a), a2+6a+5=0, a=-5 или a=-1.
Если a=-5, то y=-6x–19 – уравнение касательной.
Если a=-1, y=2x+5 – уравнение касательной.
Ответ: y=-6x–19, y=2x+5.

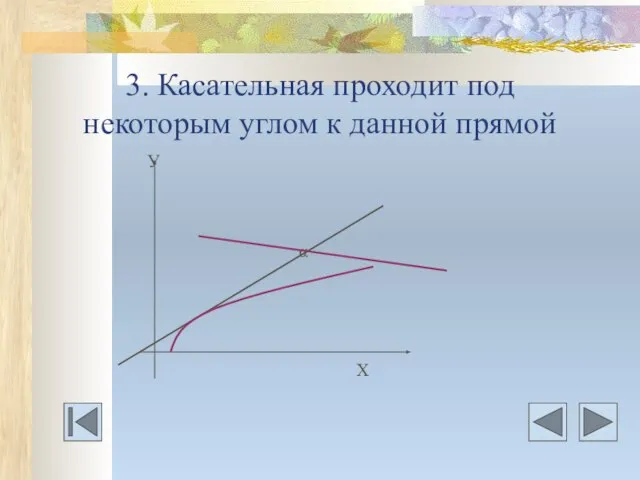
3. Касательная проходит под некоторым углом к данной прямой
У
α
Х

Даны дифференцируемая функция у=f(х) и
1) значение производной в точке касания f’(а);
2) указан угловой коэффициент касательной;
3) задан угол, между касательной к графику функции и данной прямой.

Решая уравнение f’(a)=k или f’(a)=tgα (если задан угол α) находим возможные значения а.

Ключевая задача 3. Напишите уравнения всех касательных к графику функции у=х2–2х–8, параллельных прямой у=-4х–4.
Решение. 1. Обозначим абсциссу точки касания а.
2. Найдем f(a): f(a)=a2–2a–8.
3. Найдем f’(x) и f’(a): f’(x)=2x–2, f’(a)=2a–2.
Но, с другой стороны, f’(a)= - 4 (условие параллельности). Решив уравнение 2a–2= - 4, получим a= - 1, f(a)= - 5.
Подставим найденные числа а, f(a), в общее уравнение касательной у=f(a)+f’(a)(x-a): y=-5–4(x+1),
y= - 4x–9 – уравнение касательной.
Ответ: y= - 4x–9.

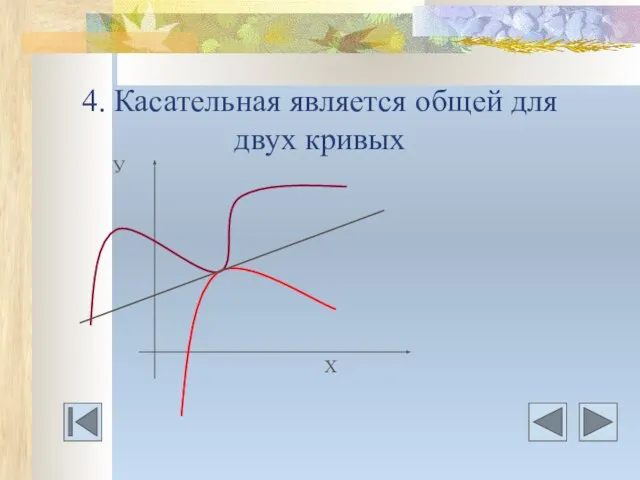
4. Касательная является общей для двух кривых
У
Х

Даны дифференцируемые функция у=f(х) и y=g(x). Нужно найти уравнения общих касательных к графику этих функций.

1 способ.
Такие задачи можно решать с помощью необходимого и достаточного признака того, что прямая у=kх+b является касательной к графику функции у=f(х) и у=g(х). Тогда задача сводится к решению системы:
f(m)=km+b,
g(n)=kn+b,
f’(m)=k,
g’(n)=k,
где (m;f(m)) и (n;g(n)) – точки касания искомой прямой с графиками функций у=f(х) и у=g(х) соответственно. Решив систему, получим возможные значения k и b и запишем уравнения общих касательных в виде у=kх+b.

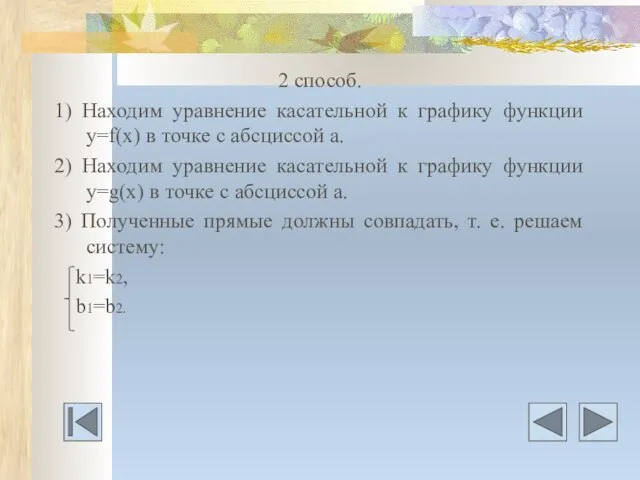
2 способ.
1) Находим уравнение касательной к графику функции у=f(х) в точке с абсциссой а.
2) Находим уравнение касательной к графику функции у=g(х) в точке с абсциссой а.
3) Полученные прямые должны совпадать, т. е. решаем систему:
k1=k2,
b1=b2.

Ключевая задача 4. Напишите уравнения всех общих касательных к графикам функций у=х2+х+1 и. у=0,5(х2+3).
Решение. I 1. а – абсцисса точки касания графика функции у=х2+х+1
2. Найдем f(a): f(a) =a2+а+1.
3. Найдем f’(x) и f’(a): f’(x)=2x+1, f”(a)=2a+1.
4. Подставим а, f(a), в общее уравнение касательной
у=f(a)+ f’(a)(x–a): y=a2+а+1+(2a+1)⋅(x–a), y=(2a+1)x–a2+1 – уравнение касательной.
II. 1. с – абсцисса точки касания графика функции у=0,5(х2 +3).
2. Найдем f(c): f(c)=0,5c2 +1,5.
3. Найдем f’(x) и f’(c): f’(x)=х, f’(c)=c.
4. Подставим а, f(a), в общее уравнение касательной у=f(a)+ f’(a)(x–a):
y=0,5c2+1,5+c(x–c), y=cx–0,5c2+1,5 – уравнение касательной.
Так как касательная общая, то 2a+1=c, c=1, с=-3
–a2+1= –0,5c2+1,5 a=0; или а=-2
Итак, y=x+1 и y=-3x–3 общие касательные.
Ответ: y=x+1 и y=–3x–3.

Является ли данная прямая касательной к графику функции у=f(x)?
Даны дифференцируемая функция у=f(х) и уравнение прямой у=kх+b. Выясните, является ли данная прямая касательной к графику функции у=f(x).

1 способ.
Если у=kх+b – уравнение к графику функции в точке с абсциссой а, то f’(а)=k. Решив это уравнение, находим а и задача сводится к решению первого типа задач на касательную. Полученное уравнение сравнивается с данным уравнением прямой.

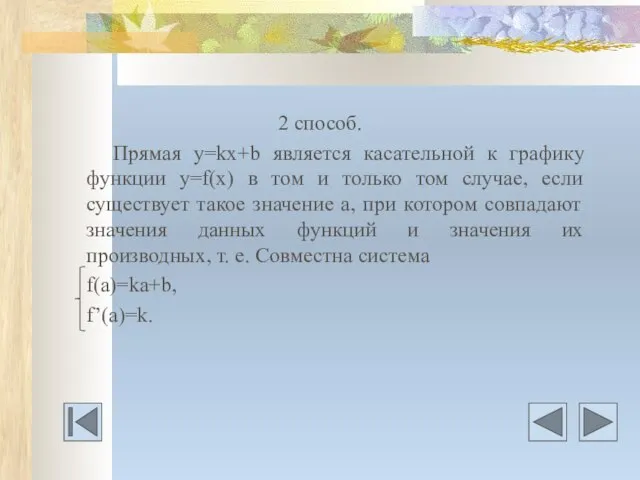
2 способ.
Прямая у=kх+b является касательной к графику функции у=f(x) в том и только том случае, если существует такое значение а, при котором совпадают значения данных функций и значения их производных, т. е. Совместна система
f(a)=ka+b,
f’(a)=k.

Представим разработанную систему задач в виде схемы.