Показательная функция

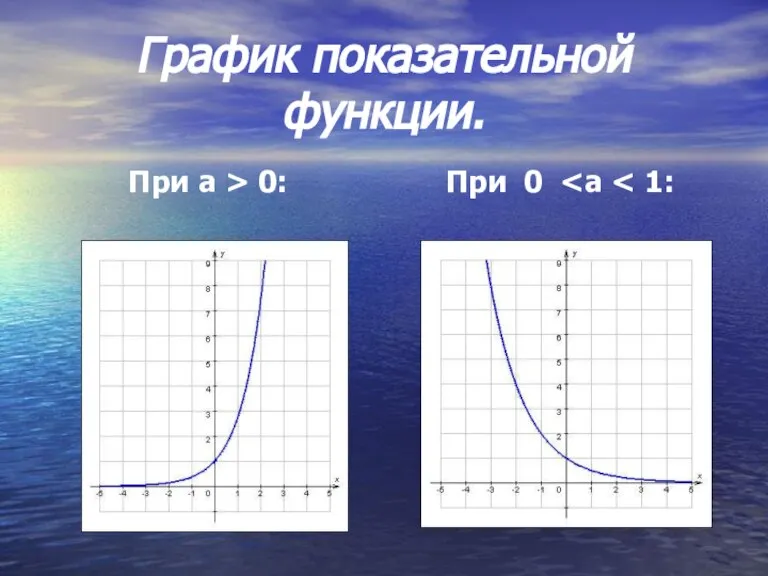
График показательной функции.
При 0 <а < 1:
При а > 0:

Свойства показательной функции
при а>0:
1.Область определения – множество действительных чисел.
2.Область значений – множество положительных действительных чисел.
3.Функция возрастает на всей числовой прямой.
4.При х = 0, у = 1, график проходит через точку (0; 1)
при 0 < а < 1:
1. Область определения – множество действительных чисел.
2. Область значений – множество положительных действительных чисел.
3. Функция убывает на всей числовой прямой.
4. При х = 0, у = 1, график проходит через точку ( 0 ; 1).

Свойства функции
При а >1, 0 < а <1 справедливы равенства:
1. ах · ау = ах+у
2. ах : ау = ах-у
3. (а ·в)х = ах · вх 4. (а/в)х = ах/ вх
5. (ах)у = аху

Выполни самостоятельно!
1. Постройте график функции
у = 3х
2. Сравните числа: 1. 4 ² и 4³
2. (0,3)2 и ( 0,3)-3
3. Вычислите:
1. 21,3 · 2-0,7 · 40,7
2. (27· 64 )1/3

Показательные уравнения
Показательными уравнениями называются уравнения вида
аf(x) = аq(x), где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому уравнению.

Способы решения показательных уравнений

Первый способ
Приведение обеих частей уравнения к одному и тому же основанию.
Пример:
2х = 32,
так как 32= 25, то имеем:
2х = 25
х = 5.

Второй способ
Путем введения новой переменной приводят уравнение к квадратному.
Пример: 4х + 2х+1 – 24 = 0
Решение:
Заметив , что 4х=(22 )х=( 2х)2 и
2х+1 = 2х × 21 , запишем уравнение в виде:
(2х )2 + 2×2х – 24 = 0,
Введем новую переменную 2х = у;
Тогда уравнение примет вид:
У2 + 2у – 24 = 0
Д = в2 – 4 а с = 22 – 4×1×(–24)
= 100> 0, находим у1 = 4, у2 = – 6.
Получаем два уравнения:
2х= 4 и 2х = – 6
22 = 22 корней нет.
х = 2.

Третий способ
Вынесение общего множителя за скобки.
Пример:
3х –– 3х+3 = –78
3х –3х ×33 = –78
3х ( 1 –33 ) = –78
3х ( – 26) = – 78
33 = – 78 : ( –26)
3х = 3
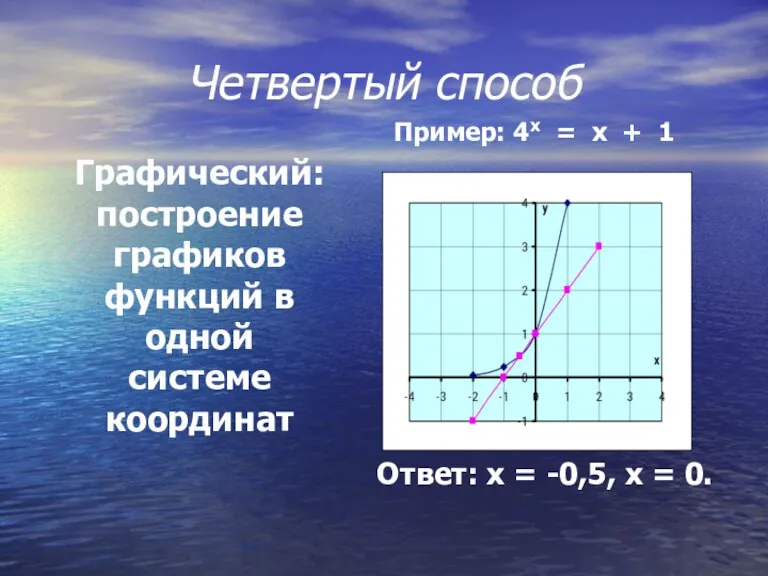
Х = 1.

Четвертый способ
Ответ: х = -0,5, х = 0.
Графический:
построение графиков функций в одной системе координат
Пример: 4х = х + 1

Выполните самостоятельно!
Решите уравнения:
1) (⅓)х+2 = 9
2) 2х-1 = 1
3) 2 ·22х– 3 · 2х - 2 = 0
4) 2х = х + 3
5) 4х+1 + 4х = 320

Показательные неравенства
Показательными неравенствами называются неравенства вида
аf(x) > аg(x) , где а – положительное число, отличное от нуля, и неравенства, сводящиеся к этому виду f(x) > q(x).

Свойства показательной функции
Если а > 0,
то показательное неравенство
аf (x) > аg (x) равносильно неравенству того же смысла
f(x) > q(x).
Если 0 < а < 1 ,
то показательное неравенство
аf (x) > аg (x) равносильно неравенству противоположного смысла
f(x) < q(x).

Решение показательных неравенств
22х-4 > 64
22х-4 > 26
2х – 4 > 6
2х > 10
х > 5
Ответ: х > 5
(0,2)х ≥ 0,04
(0,2)х ≥ (0,2)2
х ≤
Ответ: х ≤ 2

Выполни самостоятельно!
1. 45-2х ≤ 0,25
2. 0,37+4х > 0,027
3. 2х + 2х+2 < 20
4. 112х+3 ≥ 121
5. 54х+2 ≤ 125