Содержание
- 2. Содержание Введение Определение и свойства инвертных точек. Метод инверсии. 3.1. Инверсия относительно оси ОХ. 3.2. Построение
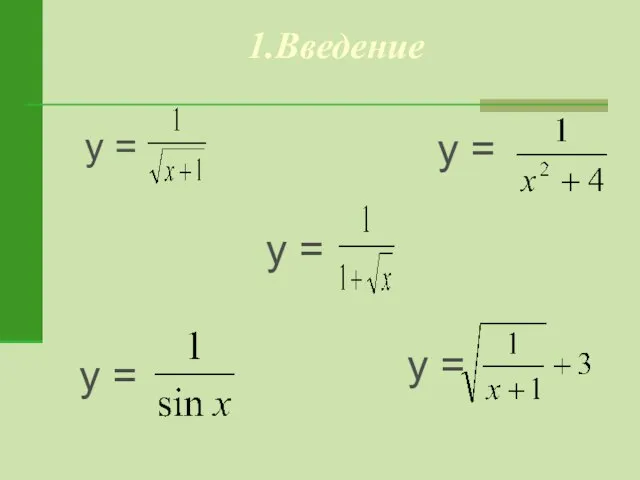
- 3. 1.Введение у = у = у =
- 4. Инверсия - изменение нормального положения компонентов, расположение их в обратном порядке. (Толковый словарь С.И. Ожегова). Инверсия
- 5. Цель работы: Изучить метод инверсии и его применение при построении графиков функций и графическом решении уравнений
- 6. Задачи: Знакомство с методом инверсии. Рассмотрение инверсии относительно прямой, осей координат. Изучение свойств инверсии. Практическое применение
- 7. Достоинства способа: он помогает приобрести навык построения графиков функций; он помогает усвоению таких важных свойств функций
- 8. 2. Определение и свойства инвертных точек. Точка В называется инвертной точке А относительно прямой (оси) е,
- 9. Преобразование плоскости, при котором каждая точка переходит в инвертную ей относительно данной прямой, называется инверсией .
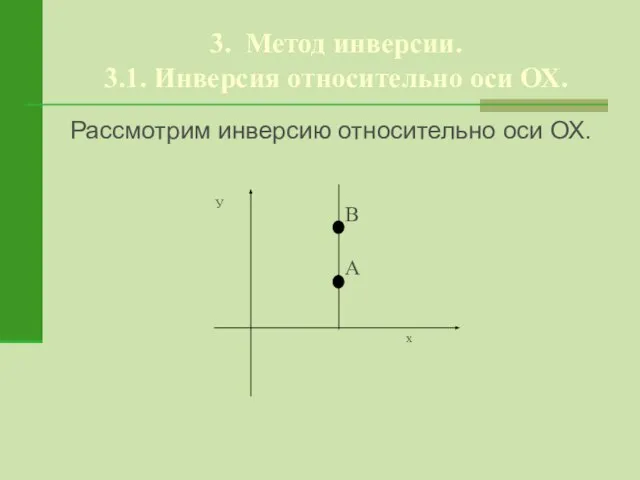
- 10. 3. Метод инверсии. 3.1. Инверсия относительно оси ОХ. Рассмотрим инверсию относительно оси ОХ.
- 11. (х ; у) (х ; ). График функции g(x)= получается из графика функции y=f(x) инверсией относительно
- 12. Свойства инверсии относительно оси Ох 1. Если f(x)>0, то >0. Если f(x) 2. Если y=f(x) имеет
- 13. 4.Если f( -x)= f(x), то g(- x)= = = g(x) Если f( -x)= - f(x), то
- 14. 7.Наибольшее значение функции изменяется и становится наименьшим, и наоборот. Максимум становится минимумом, и наоборот 8. Если
- 15. 3.2. Построение графиков y=1/f(x). Алгоритм построения: 1.Строим график функции y=f(x). 2.Через точки пересечения графика функции y=f(x)
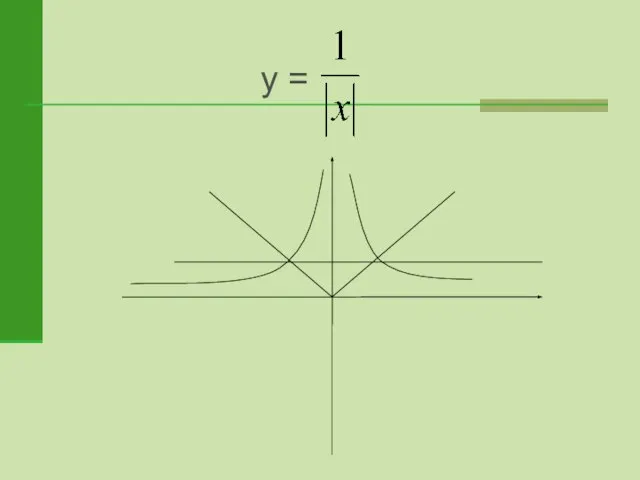
- 16. у =
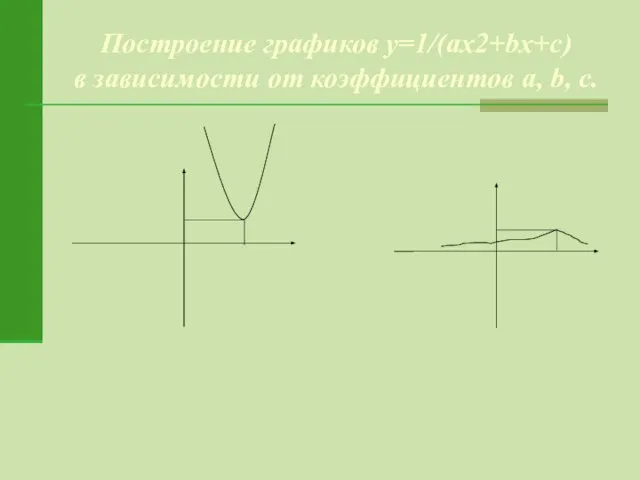
- 17. Построение графиков y=1/(ax2+bx+c) в зависимости от коэффициентов a, b, c.
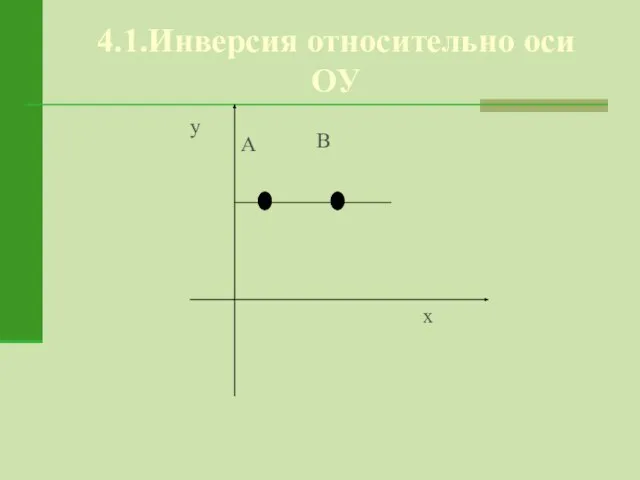
- 18. 4.1.Инверсия относительно оси ОУ
- 19. (х ; у) ( График функции g(x)=f( ) получается из графика функции y=f(x) инверсией относительно оси
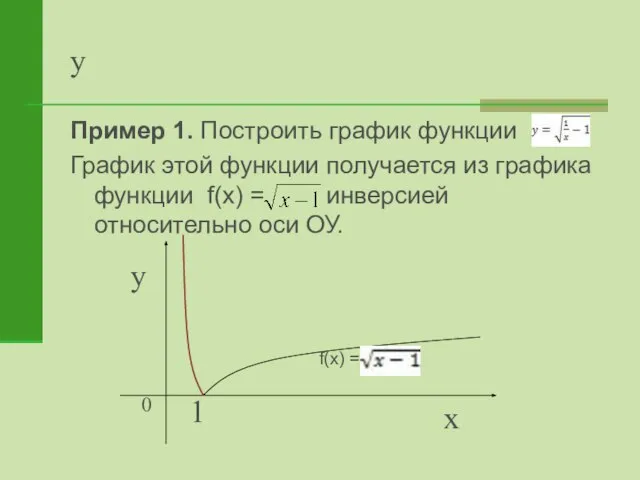
- 20. y Пример 1. Построить график функции График этой функции получается из графика функции f(x) = инверсией
- 21. 5. Применение инверсии в решении уравнений с параметром графическим способом. Рассмотренная тема находит свое применение в
- 22. С помощью графика установить: а) при каких значениях параметра а уравнение не имеет решения; б) при
- 23. Список используемой литературы А.П. Карп «Даю уроки математики» (М., «Просвещение», 1992) Н.Я. Виленкин «Алгебра 9» (учебное
- 25. Скачать презентацию
















 План урока
План урока В мире животных. Всё о бобрах
В мире животных. Всё о бобрах Свойства функции
Свойства функции ааапмп
ааапмп Построение графика линейной функции вида у= kx + b
Построение графика линейной функции вида у= kx + b Линейные уравнения с параметром
Линейные уравнения с параметром Элементы комбинаторики
Элементы комбинаторики Логарифмическая функция и ее применение
Логарифмическая функция и ее применение Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости 7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска
7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска  Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Квадратный корень
Квадратный корень Неопределенный интеграл
Неопределенный интеграл Функция Презентация выполнена учителем математики МБОУ СОШ № 22 Т. П. Лисицыной, п. Пересыпь, Темрюкского района, Краснодарс
Функция Презентация выполнена учителем математики МБОУ СОШ № 22 Т. П. Лисицыной, п. Пересыпь, Темрюкского района, Краснодарс Preobrazovanie-grafikov-trigonometricheskih-funkciy.ppt
Preobrazovanie-grafikov-trigonometricheskih-funkciy.ppt Презентация на тему Становление современной естественнонаучной картины мира
Презентация на тему Становление современной естественнонаучной картины мира  Крестовые походы
Крестовые походы Решение рациональных уравнений
Решение рациональных уравнений Линейные уравнения ax=b
Линейные уравнения ax=b Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  Логарифм числа
Логарифм числа Квадратные уравнения 8 класс
Квадратные уравнения 8 класс Презентация на тему Требования к гос. служащим
Презентация на тему Требования к гос. служащим  pervoobraznaya-i-neopredelennyy-integral.pptx
pervoobraznaya-i-neopredelennyy-integral.pptx Презентация на тему Порядок и особенности прохождения государственной службы в таможенных
Презентация на тему Порядок и особенности прохождения государственной службы в таможенных  ВПК России 1
ВПК России 1 Применения непрерывности Метод интервалов
Применения непрерывности Метод интервалов