Teorema-Vieta.ppt

Основная цель – изучить теорему Виета и ей обратную, уметь применять при решении квадратных уравнений
«Вся математика – это,
собственно, одно большое
уравнение для других наук»
Новалис
Девиз урока:

Устная работа
x² + 4x - 6 = 0
2x² + 6x = 6
7x² - 14x = 0
x² + 5x - 1= 0
3x² - 5x + 19 = 0
x² - 13x = 0

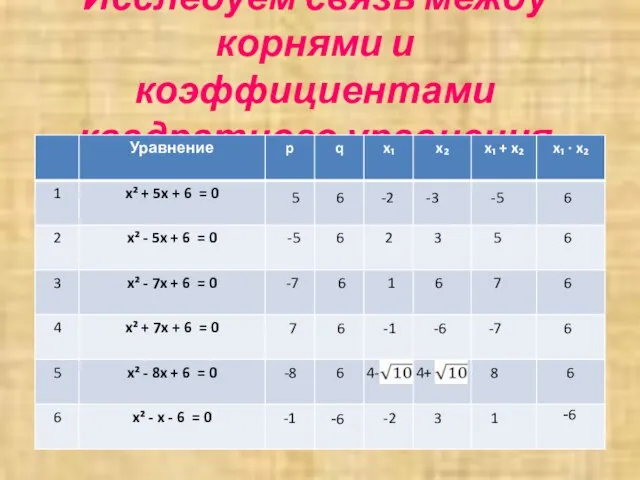
Исследуем связь между корнями и коэффициентами квадратного уравнения
5
-5
-7
7
-8
-1
6
6
6
6
6
-6
-2
-3
-5
6
2
3
5
6
1
6
7
6
-1
-6
-7
6
4-
4+
8
6
-2
3
1
-6

Дано: х₁ и х₂ - корни уравнения
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x² + px + q =0
Доказать:
х₁ + х₂ = -p,
х₁ ∙ х₂ = q
Теорема Виета

План доказательства:
Записать формулы для нахождения x₁и x₂;
Найти сумму корней: x₁+ x₂;
Найти произведение корней: x₁· x₂.
Теорема Виета

Теорема Виета
Доказательство:
х ² + pх + q = 0
1. х₁ =
, х₂ =
=
=
= -p
3. x₁ ∙ x₂ =
∙
=
=
=
, D = p² -4q.
=
=
= q
2. x₁+x₂=
+
=

1.Определите, верно ли сформулирована теорема: Сумма корней квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену
2. Для всех ли приведенных уравнений x₁+ x₂= -p
x₁· x₂= q
3. Сформулируйте теорему со словами «Если…, то…»

Что позволяет находить доказанная теорема?
Что должно быть известно до применения теоремы?

Можно ли найти сумму и произведение корней следующих уравнений
х² + 3х + 6 = 0
х² + 5 = 0
2х² – 7х + 5 = 0

x² + px + q = 0
x² - (х₁ + х₂)х + х₁ ∙ х₂ = 0
Задание 1. Выберите уравнение сумма корней которого равна -6, а произведение равно -11
х² - 6х + 11 = 0
х² + 6х - 11 = 0
х² + 6х + 11 = 0
х² - 11х - 6 = 0
х² + 11х - 6 = 0

Задание 2. Если х₁ = -5 и х₂ = -1 - корни уравнения х² + px +q = 0, то
1) p = -6, q = -5
2) p = 5, q = 6
3) p = 6, q = 5
4) p = -5, q = -6
5) p = 5, q = -6
6) p = -6, q = -5

Задание 3. Найдите сумму и произведение корней уравнения х² - 3х - 5 = 0.
Выберите правильный ответ.
х₁ + х ₂= -3, х₁ ∙ х₂ = -5
х₁ + х ₂= -5, х₁ ∙ х₂ = -3
х₁ + х ₂= 3, х₁ ∙ х₂ = -5
х₁ + х ₂= 5, х₁ ∙ х₂ = -3

Найти сумму и произведение корней уравнения
Решение:
б) y² – 19 =0, D > 0
p = 0, q = - 19
х₁ + х ₂= 0, х₁ ∙ х₂ = -19
д) 2x² – 9x – 10 = 0
х² – 4,5х – 2 = 0,
D > 0
p = - 4,5, q = - 2
х₁ + х ₂= 4,5, х₁ ∙ х₂ = -2
№573
а) в) у доски
г) д) самостоятельно с последующей проверкой
:2

Для каждого уравнения укажите, если это возможно сумму и произведение корней
х² – 2х – 8 = 0
Для каждого уравнения попытайтесь подобрать два числа х₁ и х₂ так, чтобы выполнялись получившиеся равенства.
2. х² + 7х + 12 = 0
3. y² – 8y – 9 = 0
D > 0, p = -2, q = -8
x₁ + x₂ = 2
x₁ ∙ x₂ = -8
D > 0, p = 7, q = 12
x₁ + x₂ = -7
x₁ ∙ x₂ = 12
D > 0, p = -8, q = -9
y₁ + y₂ = 8
y₁ ∙ y₂ = -9
x₁ = -2
x₂ = 4
2 ∙ (-4)
-2 ∙ 4
1 ∙ (-8)
-1 ∙ 8
Проверьте, будут ли полученные числа корнями данного уравнения
x₁ = -3
x₂ = -4
y₁ = -1
y₂ = 9

Прямая теорема:
Если х₁ и х₂ - корни уравнения
х² + px + q = 0.
Тогда числа х₁, х₂ и p, q связаны равенствами
Обратная теорема:
Если числа х₁, х₂ и p, q связаны равенствами
х₁ + х₂ = -p,
х₁ ∙ х₂ = q.
Теорема Виета
х₁ + х₂ = -p,
х₁ ∙ х₂ = q
Тогда х₁ и х₂ - корни уравнения
х² + px + q = 0.
Числа х₁ и х₂ являются корнями приведенного квадратного уравнения х² + px +q = 0 тогда и только тогда, когда
x₁ +х₂ = - p, x₁ ∙ x₂ = q

Применение теоремы
Проверяем, правильно ли найдены корни уравнения
Определяем знаки корней уравнения не решая его
Устно находим корни приведенного квадратного уравнения
Составляем квадратное уравнение с заданными корнями

Теорема Виета
Числа х₁ и х₂ являются корнями квадратного уравнения х² + вх + с =0
тогда и только тогда, когда
х₁ + х₂ =
х₁ ∙ х₂ =
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — и дробь уж готова?
В числителе с, в знаменателе а
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.

Домашнее задание:
п. 23 (знать теорему Виета),
дифференцированное задание
(листок с домашней работой)