«Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе

Умение решать задачи – практическое искусство,
подобное плаванию или катанию на лыжах, или
игре на фортепиано;
научиться этому можно
лишь подражая избранным образцам и постоянно тренируясь.
Д. Пойа.

В мире интересного
Французское слово «десерт» означает сладкие блюда, подаваемые в конце обеда. Названия некоторых десертов, пирожных и мороженного, также имеют французское происхождение. Например, мороженое «пломбир» получило свое название от французского города Пломбьер. Где оно впервые было изготовлено по особой рецептуре.

Узнайте, как переводится французское слово «безе» (легкое пирожное из взбитых яичных белков и сахара)?

Найдите сумму одиннадцати членов арифметической прогрессии, первый член которой равен – 5, а шестой равен – 3,5.

молния - перевод французского слова «эклер» (пирожное из заварного теста с кремом внутри).

Прогрессии в жизни и быту
В природе все продумано
и совершенно.

Вертикальные стержни фермы имеют следующую длину: наименьший
5 дм., а каждый следующий – на 2 дм. длиннее. Найдите длину семи таких стержней.
Ответ: 77 дм.

В благоприятных условиях бактерия размножается так, что за 1 секунду делится на три. Сколько бактерий будет в пробирке через 5 секунд?
Ответ: 121

Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено на девятый день, если вся работа была выполнена за 14 дней.
18 тонн

Тело падает с башни, высотой 26 м. В первую секунду проходит 2м, а за каждую следующую секунду – на 3 м больше, чем за предыдущую. Сколько секунд пройдет тело до удара о землю?
Ответ: 4 секунды

За первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
Ответ: 30 дней

Из пункта А выехал грузовой автомобиль со скоростью 40 км/ч. Одновременно из пункта В навстречу ему отправился второй автомобиль, который в первый час прошел 20 км, а каждый следующий проходил на 5 км больше, чем в предыдущий. Через сколько часов они встретятся, если расстояние от А до В равно 125 км?
Ответ: 2 часа

Амфитеатр состоит из 10 рядов, причем в каждом следующем ряду на 20 мест больше, чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?
Ответ:1900

Немного истории
Задачи на геометрические и арифметические прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах».

На связь между прогрессиями первым обратил внимание Архимед.

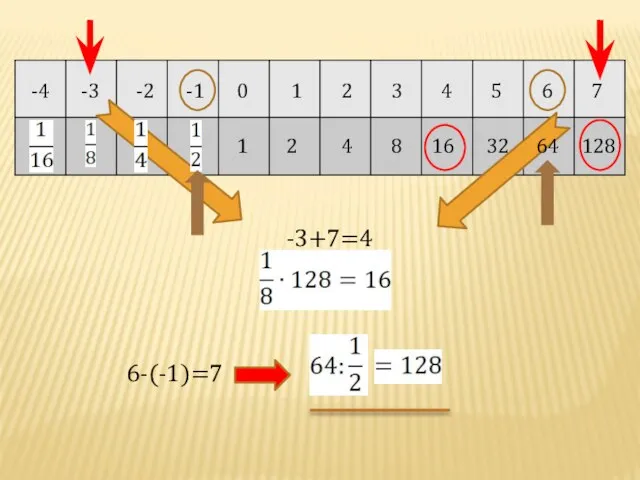
В 1544 г. вышла книга немецкого математика М. Штифеля «Общая арифметика». Штифель составил такую таблицу:

128
-3
7
-3+7=4
4
16
-4
-2
-1
0
1
2
3
5
6
64
6-(-1)=7
32
1
2
4
8

а
б
д
е
в
г
ж
кросснамбер

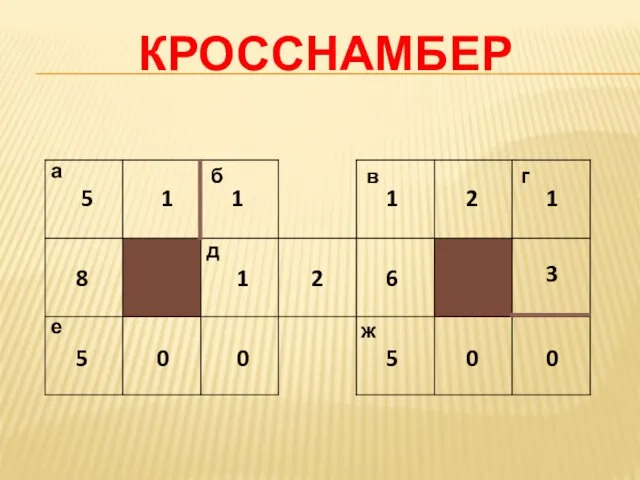
кросснамбер
5
1
1
2
1
1
2
6
5
0
0
5
0
0
8
1
3
а
б
в
г
д
е
ж

Решение задач

1. Дана геометрическая прогрессия 3; b2; b3;…, знаменатель которой - целое число. Найдите эту прогрессию, если
Решение:
b2=3q, b3=3q2
, q=-5; -4; -3; -2; -1
3; -15; 75
3; -12; 48;…
3; -9; 27;…
3; -6; 12;…
3; -3; 3;…
Ответ:

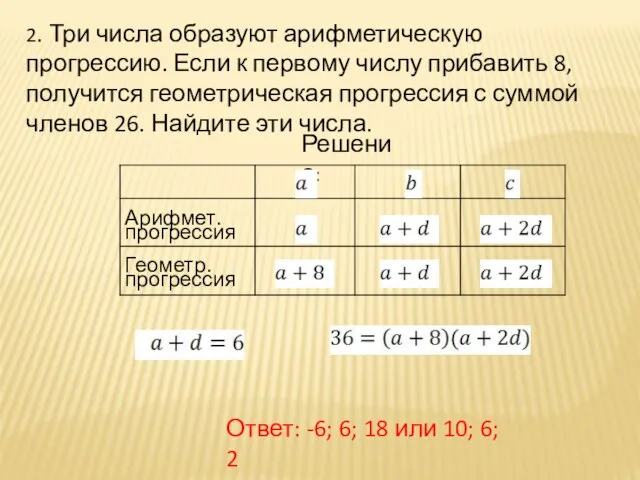
2. Три числа образуют арифметическую прогрессию. Если к первому числу прибавить 8, получится геометрическая прогрессия с суммой членов 26. Найдите эти числа.
Решение:
Ответ: -6; 6; 18 или 10; 6; 2

3. Уравнение имеет корни , а уравнение
– корни . Определите k и m, если числа – последовательные члены возрастающей геометрической прогрессии.
подсказка
Решение:
- геометрическая прогрессия
Ответ: k=2, m=32

Теорема Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.