Решение неравенств второй степени

Цель урока
Обобщить, систематизировать и расширить знания по теме «Решение неравенств второй степени с одной неизвестной».

ХОД ИССЛЕДОВАНИЯ:
Определение неравенств второй степени
Методы решения неравенств:
Графический:
Решение неравенства второй степени при
Метод интервалов

Определение неравенств второй степени:
Неравенства вида
где х – переменная, a, b и с некоторые числа, причем , называют неравенствами второй степени с одной переменной.

Графический метод решения неравенств:
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
При решении неравенства графическим способом важно знать как направлены ветви параболы – вверх или вниз и каковы абсциссы точек её пересечения с осью х, координаты вершины параболы нас не интересуют.

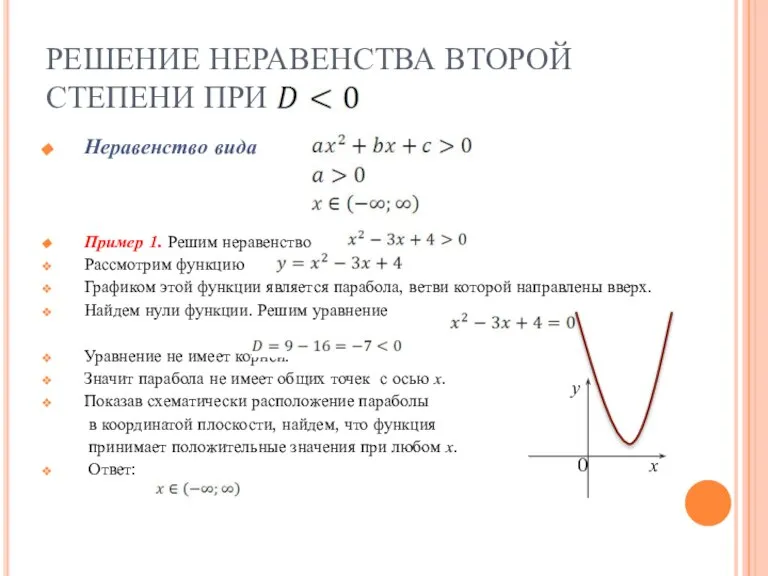
РЕШЕНИЕ НЕРАВЕНСТВА ВТОРОЙ СТЕПЕНИ ПРИ
Неравенство вида
Пример 1. Решим неравенство
Рассмотрим функцию
Графиком этой функции является парабола, ветви которой направлены вверх.
Найдем нули функции. Решим уравнение
Уравнение не имеет корней.
Значит парабола не имеет общих точек с осью х.
Показав схематически расположение параболы
в координатой плоскости, найдем, что функция
принимает положительные значения при любом х.
Ответ:
х
у
0

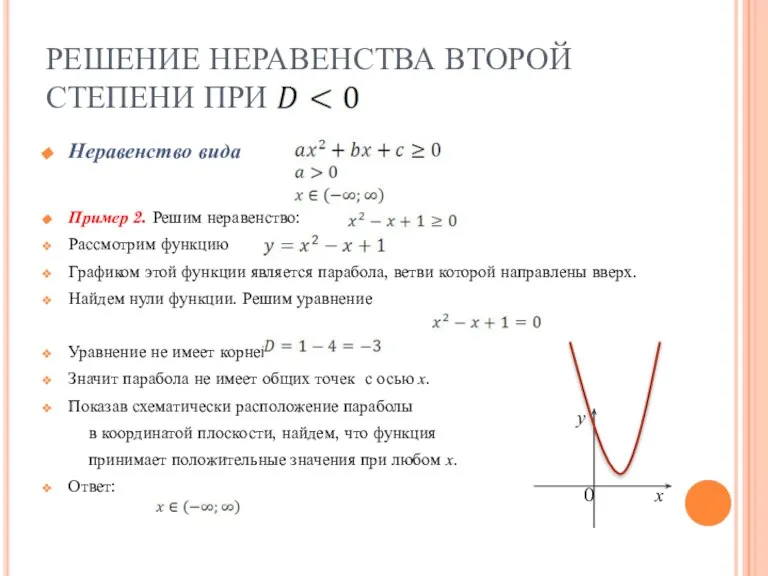
РЕШЕНИЕ НЕРАВЕНСТВА ВТОРОЙ СТЕПЕНИ ПРИ
Неравенство вида
Пример 2. Решим неравенство:
Рассмотрим функцию
Графиком этой функции является парабола, ветви которой направлены вверх.
Найдем нули функции. Решим уравнение
Уравнение не имеет корней.
Значит парабола не имеет общих точек с осью х.
Показав схематически расположение параболы
в координатой плоскости, найдем, что функция
принимает положительные значения при любом х.
Ответ:
х
у
0

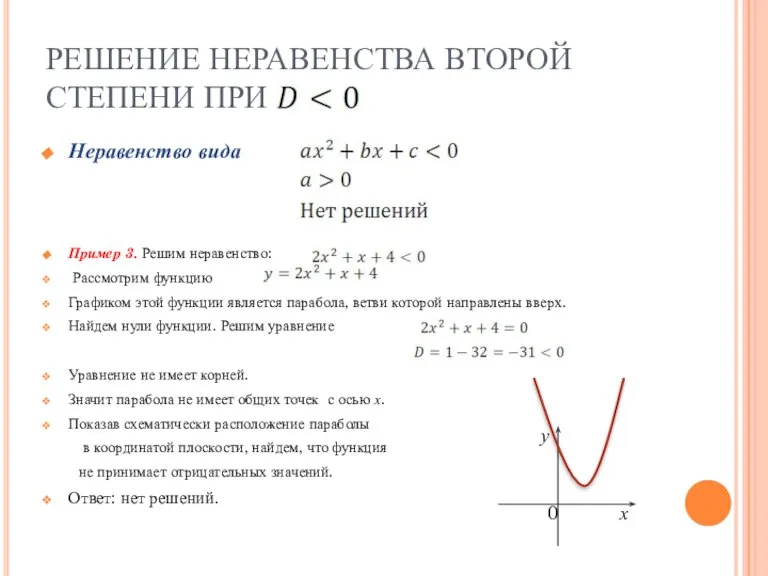
РЕШЕНИЕ НЕРАВЕНСТВА ВТОРОЙ СТЕПЕНИ ПРИ
Неравенство вида
Пример 3. Решим неравенство:
Рассмотрим функцию
Графиком этой функции является парабола, ветви которой направлены вверх.
Найдем нули функции. Решим уравнение
Уравнение не имеет корней.
Значит парабола не имеет общих точек с осью х.
Показав схематически расположение параболы
в координатой плоскости, найдем, что функция
не принимает отрицательных значений.
Ответ: нет решений.
х
у
0

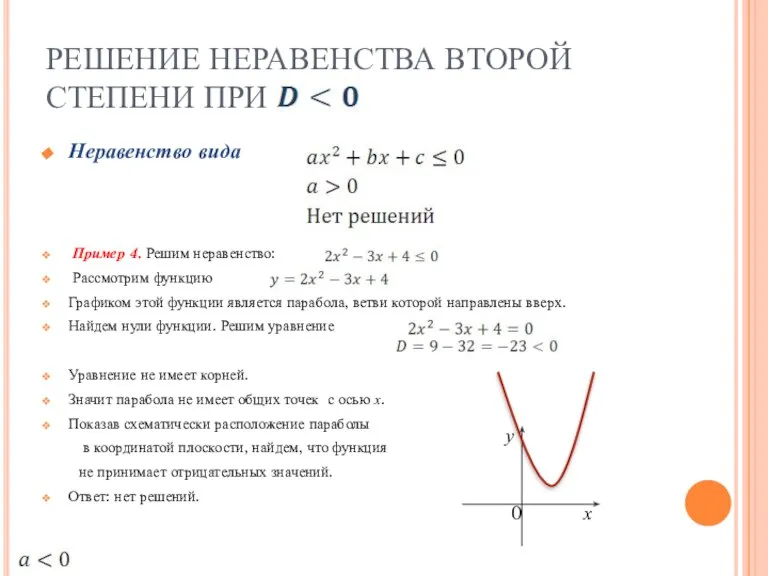
РЕШЕНИЕ НЕРАВЕНСТВА ВТОРОЙ СТЕПЕНИ ПРИ
Неравенство вида
Пример 4. Решим неравенство:
Рассмотрим функцию
Графиком этой функции является парабола, ветви которой направлены вверх.
Найдем нули функции. Решим уравнение
Уравнение не имеет корней.
Значит парабола не имеет общих точек с осью х.
Показав схематически расположение параболы
в координатой плоскости, найдем, что функция
не принимает отрицательных значений.
Ответ: нет решений.
х
у
0