Слайд 2Справимся легко!
№1. По графику функции y=f(x) ответьте на вопросы:
Сколько точек максимума имеет
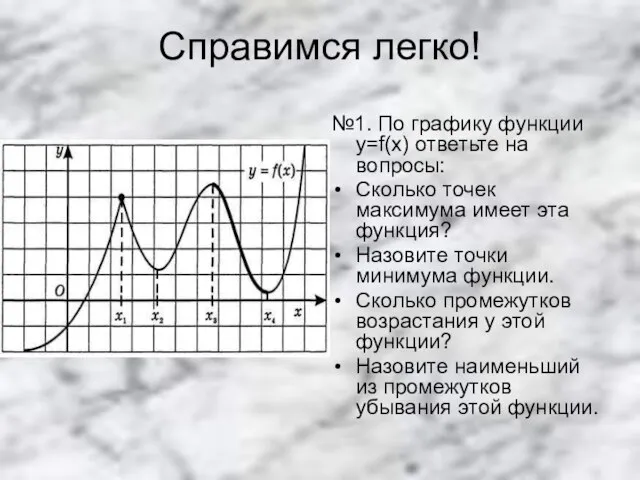
эта функция?
Назовите точки минимума функции.
Сколько промежутков возрастания у этой функции?
Назовите наименьший из промежутков убывания этой функции.
Слайд 3Легко ли?
№2. (задание В5 ЕГЭ по математике)
По графику функции
y=f ´(x) ответьте
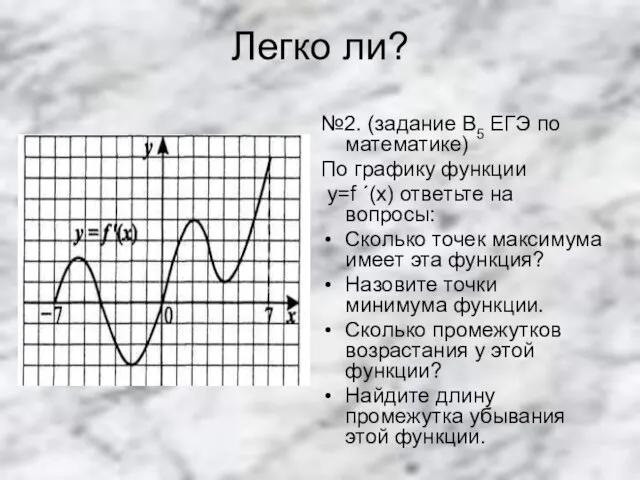
на вопросы:
Сколько точек максимума имеет эта функция?
Назовите точки минимума функции.
Сколько промежутков возрастания у этой функции?
Найдите длину промежутка убывания этой функции.
Слайд 4Для нас задача…
Составить (создать, разработать) правило (алгоритм), с помощью которого

можно исследовать функции на монотонность и экстремумы по её производной.
Слайд 7Теорема 1
Если во всех точках открытого промежутка Х производная f ´(x)

больше или равна нулю (причем
f ´(x) =0 лишь в отдельных точках), то функция y=f (x) возрастает на промежутке Х.
Слайд 8Теорема 2
Если во всех точках открытого промежутка Х производная f ´(x)

меньше или равна нулю (причем
f ´(x) =0 лишь в отдельных точках), то функция y=f (x) убывает
на промежутке Х.
Слайд 9Теорема 3
Если функция y=f (x) имеет экстремум в точке х0, то

в этой точке производная функции либо равна нулю, либо не существует.
Слайд 11
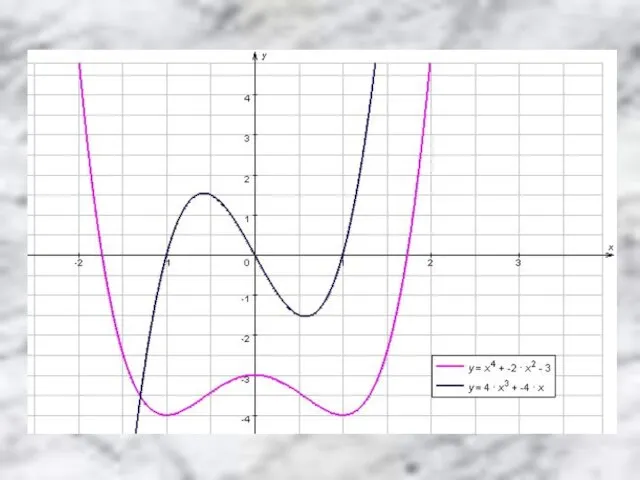
№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её
![№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/266111/slide-10.jpg)
производной. Укажите количество промежутков возрастания функции.
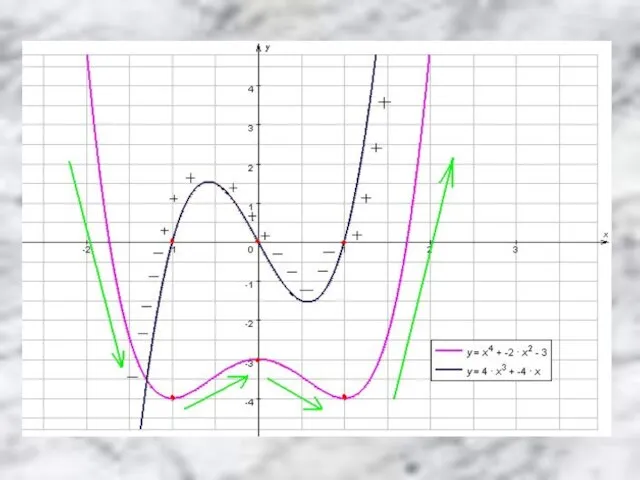
Слайд 12 №2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график
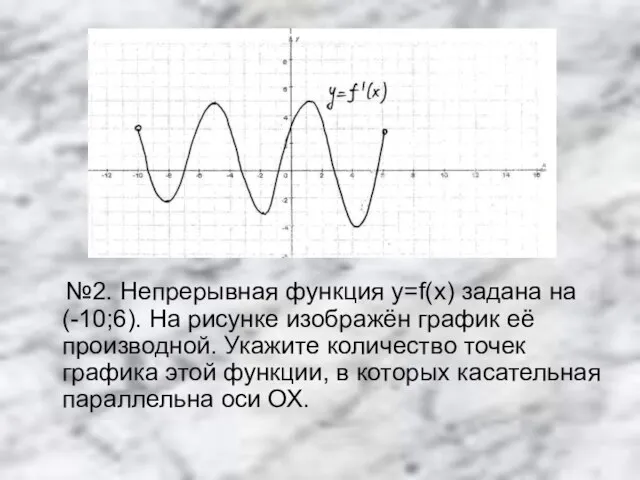
её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ.
Слайд 13 №3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график
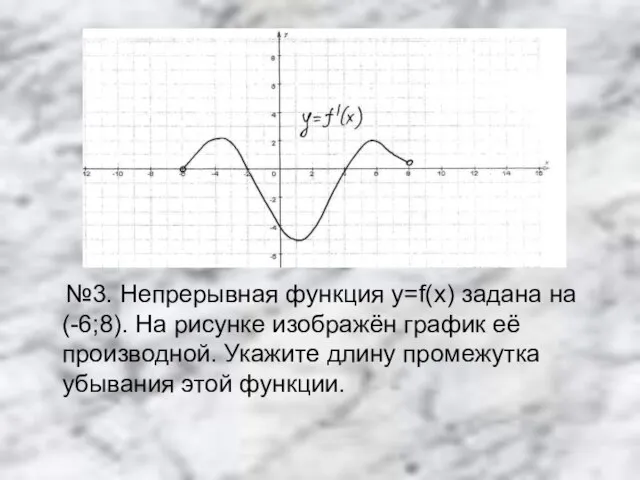
её производной. Укажите длину промежутка убывания этой функции.







![№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/266111/slide-10.jpg)


 Перестановки Урок алгебры 9 класс.
Перестановки Урок алгебры 9 класс. Одночлен енодончл
Одночлен енодончл  УРОК АЛГЕБРЫ И НАЧАЛА АНАЛИЗА В 10А КЛАССЕ ПО ТЕМЕ: «ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ»
УРОК АЛГЕБРЫ И НАЧАЛА АНАЛИЗА В 10А КЛАССЕ ПО ТЕМЕ: «ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ» Презентация на тему Методы Тагути
Презентация на тему Методы Тагути  Решение неравенств второй степени
Решение неравенств второй степени Основы логики. Алгебра высказываний
Основы логики. Алгебра высказываний Сложение и вычитание обыкновенных дробей с одинаковым знаменателем
Сложение и вычитание обыкновенных дробей с одинаковым знаменателем Решение уравнений Математика, 5 класс
Решение уравнений Математика, 5 класс  Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к
Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к МОУ «Аминевская СОШ» А.Н. Ямалетдинова- учитель математики.
МОУ «Аминевская СОШ» А.Н. Ямалетдинова- учитель математики. Решение показательных уравнений
Решение показательных уравнений Векторы (повторение)
Векторы (повторение)  Презентация на тему Особенности прохождения гос. службы в правоохранит. органах
Презентация на тему Особенности прохождения гос. службы в правоохранит. органах  Презентация на тему Путешествие в дальние страны АФРИКА
Презентация на тему Путешествие в дальние страны АФРИКА  Неравенства, содержащие модуль
Неравенства, содержащие модуль Линейная функция
Линейная функция  Экскурсия в историю математики
Экскурсия в историю математики Презентация на тему Позиции критиков норманской теории
Презентация на тему Позиции критиков норманской теории  Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Презентация на тему Театр в 18 веке в России
Презентация на тему Театр в 18 веке в России  Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов
Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов  Алгебраические дроби (8 класс)
Алгебраические дроби (8 класс) Решение линеиных неравенств
Решение линеиных неравенств Преобразование графиков функций
Преобразование графиков функций Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре Линейное уравнение с двумя переменными и его график
Линейное уравнение с двумя переменными и его график Уравнения с параметрами
Уравнения с параметрами Презентация на тему Стекло
Презентация на тему Стекло