Содержание
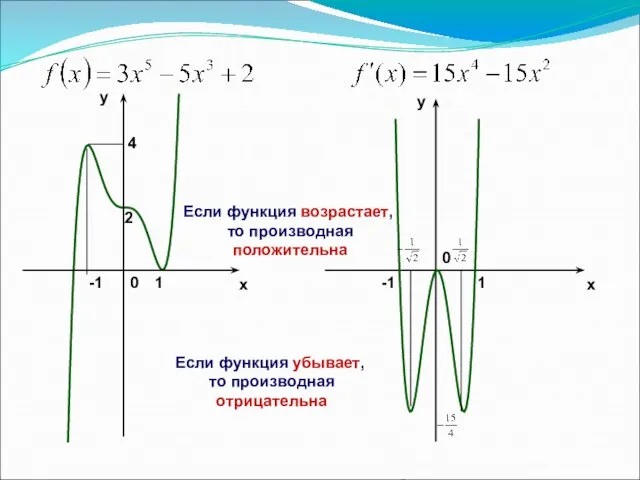
- 2. x y y x 2 -1 1 4 0 -1 1 0 Если функция возрастает, то
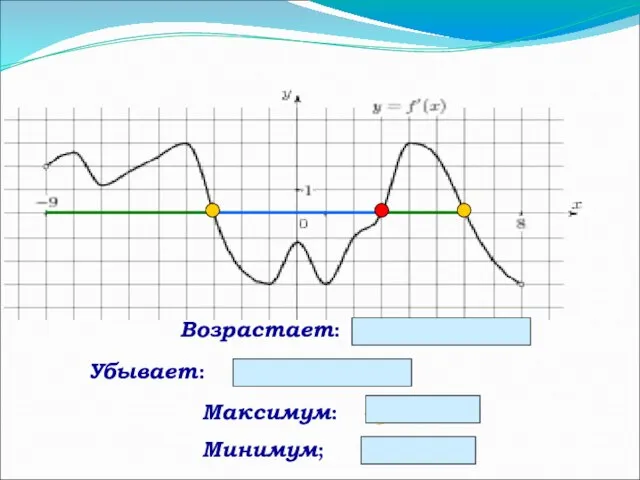
- 3. Максимум: - 3; 6 Минимум; 3 Возрастает: (-9;-3) и (3;6) Убывает: (-3;3)
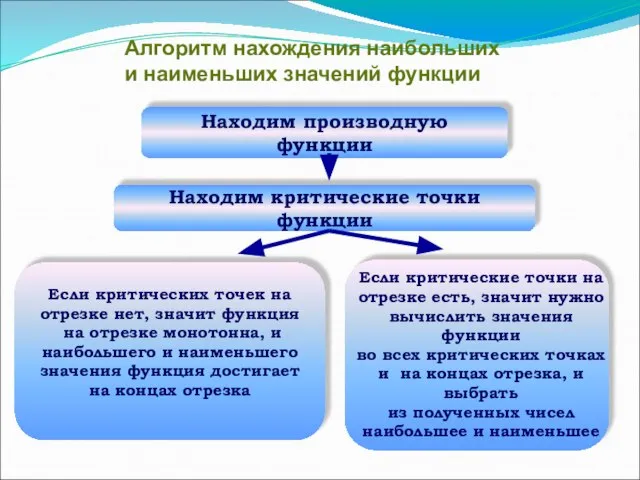
- 4. Находим производную функции Находим критические точки функции Если критических точек на отрезке нет, значит функция на
- 5. х = 1 ; х = 5/3 f(-1)=18 f(3) = 2 f(1) = 6 f(5/3) =
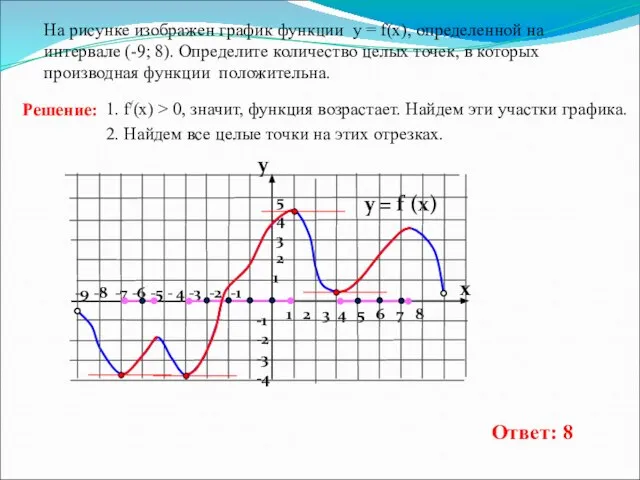
- 6. -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6
- 7. -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6
- 8. Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график. В ответе
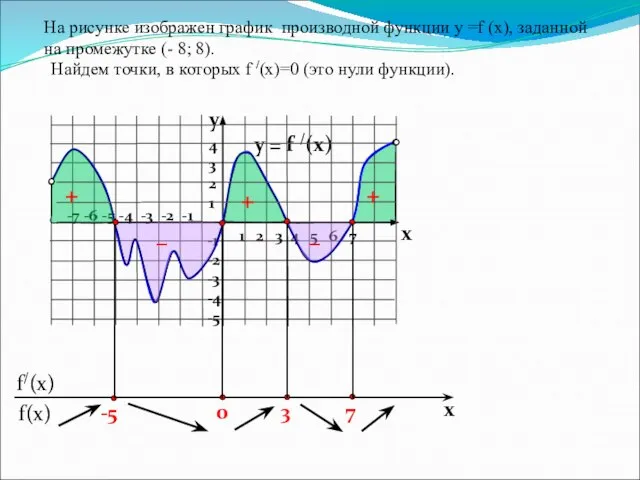
- 9. На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). y
- 10. y = f /(x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3
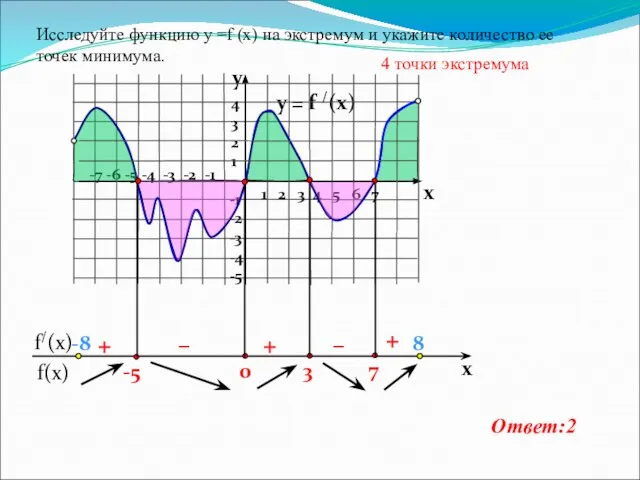
- 11. y = f /(x) 4 3 2 1 -1 -2 -3 -4 -5 y x +
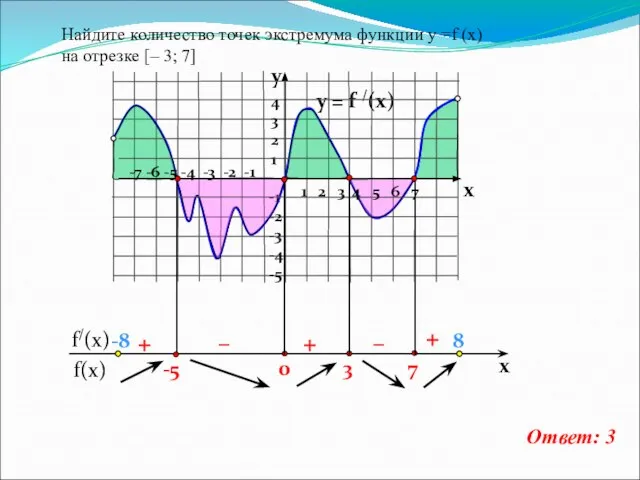
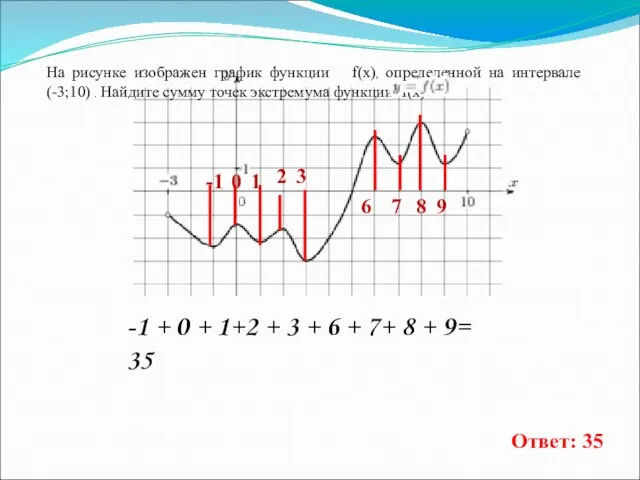
- 12. На рисунке изображен график функции f(x), определенной на интервале (-3;10) . Найдите сумму точек экстремума функции
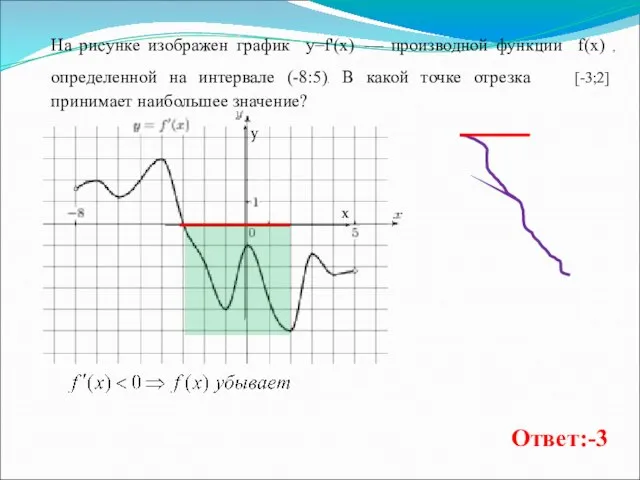
- 13. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8:5). В какой
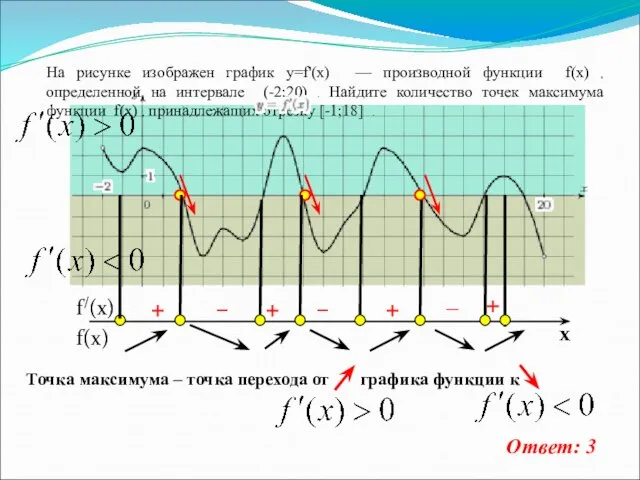
- 14. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-2;20) . Найдите
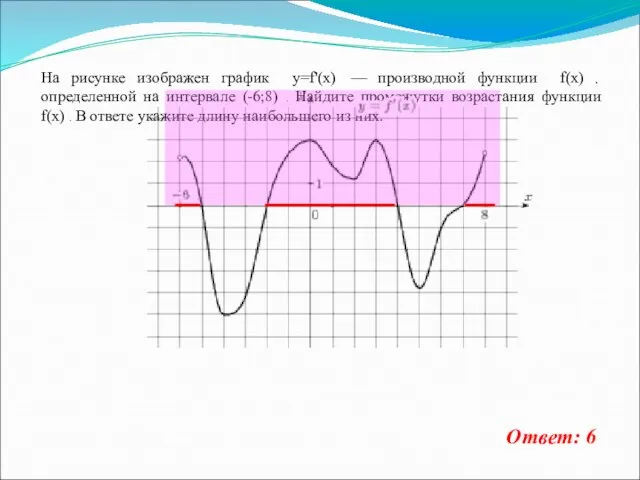
- 15. На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) . Найдите
- 17. Скачать презентацию

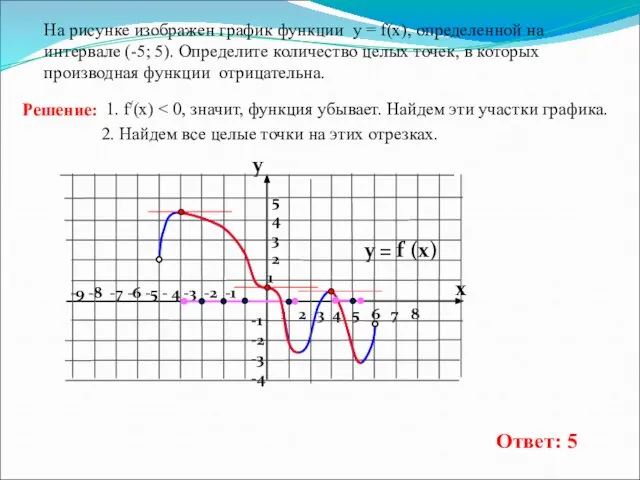
![Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304616/slide-7.jpg)
 Наглядное представление статистической информации
Наглядное представление статистической информации Элементы комбинаторики
Элементы комбинаторики Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  Презентация на тему Научно-техническая революция XXв
Презентация на тему Научно-техническая революция XXв  Primenenie-proizvodnoy-k-issledovaniyu-funkciy.ppt
Primenenie-proizvodnoy-k-issledovaniyu-funkciy.ppt Презентация на тему Анализ человеческого потенциала совета федераций
Презентация на тему Анализ человеческого потенциала совета федераций  Лекции по алгебре и началам анализа 10 класс
Лекции по алгебре и началам анализа 10 класс Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»
Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»  Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов
Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов  Квадратичная функция. функция
Квадратичная функция. функция  Презентация на тему Государственная служба и государственные служащие
Презентация на тему Государственная служба и государственные служащие  Линейная функция
Линейная функция  Презентация на тему Центральная Азия
Презентация на тему Центральная Азия  Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре Последовательности 2011 Васильева Е.Е.
Последовательности 2011 Васильева Е.Е. Линейные уравнения ax=b
Линейные уравнения ax=b Обратные тригонометрические функции
Обратные тригонометрические функции Алгебраический тренажёр
Алгебраический тренажёр Преобразование графиков функций, содержащих модуль - презентация по Алгебре
Преобразование графиков функций, содержащих модуль - презентация по Алгебре Функция y = k√x . Подкоренная функция
Функция y = k√x . Подкоренная функция РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Математика и естественные науки
Математика и естественные науки Презентация на тему Виды принципов прокурорского надзора
Презентация на тему Виды принципов прокурорского надзора  Некоторые способы умножения многочленов одной переменной
Некоторые способы умножения многочленов одной переменной Решение квадратных уравнений
Решение квадратных уравнений Решение показательных уравнений, 9 класс Урок закрепления знаний, умений и навыков Автор-составитель: учитель математики
Решение показательных уравнений, 9 класс Урок закрепления знаний, умений и навыков Автор-составитель: учитель математики  Формулы для решения квадратного уравнения
Формулы для решения квадратного уравнения