Исследование функций и построение графиков

Схема исследования функции с целью построения ее графика
1) Область определения, непрерывность, четность/нечётность.
2) Асимптоты графика функции.
3) Возрастание, убывание и экстремумы функции.
4) Выпуклость, вогнутость и перегибы графика.

Область определения функции и множество значений функции
Область определения функции(D)- это множество тех значений которые может принимать аргумент
Множество значений функции(Е)- это множество тех значений, которые может иметь сама функция при всех значениях аргумента с области определения (это все значения а, при которых уравнение f(x) = a имеет решения)
ПРИМЕР. f(x)=x-1
Область определения: x - 1 ≥ 0, то есть x ∈ [1; +∞) (Df = [1; + ∞))

Непрерывность функции
Функция f(x) называется непрерывной в точке а, если при
x → a f(x) → f(a), то есть
Если функция ƒ(x) непрерывна в каждой точке некоторого промежутка I, то ее называют непрерывной на промежутке I.
(график функции, непрерывной на промежутке — непрерывная линия на этом промежутке.)
Примеры функций, которые имеют точки разрыва
y = [x] — целая часть x
Точки разрыва — 0 — точка разрыва. 0 — точка разрыва.
все целочисленные
точки.

Четные и нечётные функции
Функция f называется парной, если её область определения симметрична относительно началу координат и для любого x из её области определения f(-x) = f (x)
Свойства
График парной функции симметричен относительно оси 0y
Функция f называется не парной, если её область определения симметрична относительно началу координат и для любого x из её области определения f(-x) = - f (x)
Свойства
График парной функции симметричен относительно началу координат

Примеры четной функции

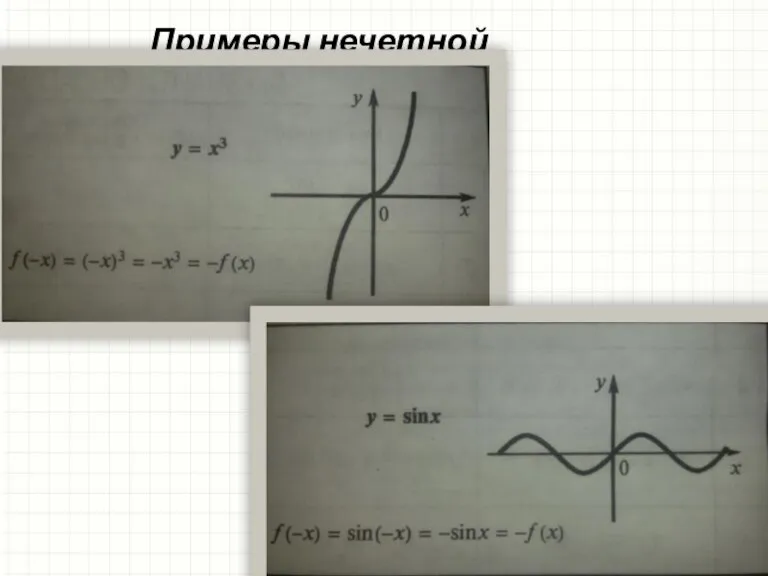
Примеры нечетной функции

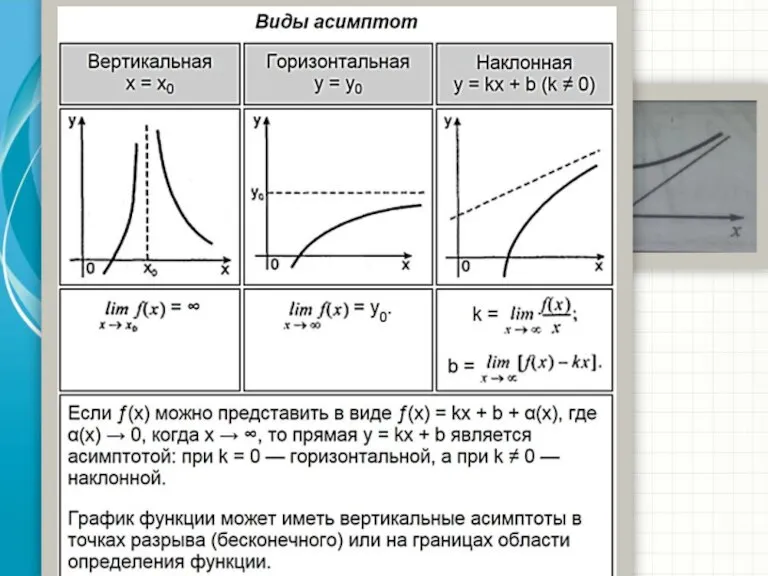
Асимптоты
Асимптота кривой- это прямая
к которой неограниченно
приближается кривая при
удалении её в бесконечность

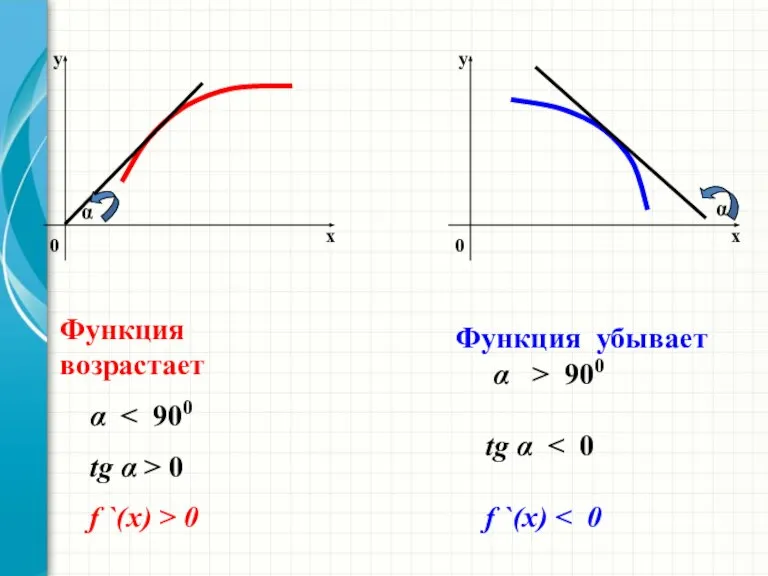
функция y = f (x) называется возрастающей на отрезке
[a, b],если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f (x) ≤ f (x'), и строго возрастающей— если выполняется неравенство f (x)< f (x'). Аналогично
определяется убывание
Например функция у = х2 (рис., а) строго возрастает на отрезке [0,1], а
(рис., б) строго убывает на этом отрезке.

Теорема. Если функция f имеет неотрицательную производную в каждой точке интервала (а;b), то функция f возрастает на интервале (а;b).
Теорема. Если функция имеет неположительную производную в каждой точке интервала (а;b), то функция f убывает на интервале (а;b).



Функция возрастает
 < 900
tg  > 0
f `(x) > 0
Функция убывает
 > 900
tg  < 0
f `(x) < 0

Исследование экстремумов функции
Необходимое условие экстремума. (теорема Ферма)
Если точка х0 является точкой экстремума функции f и в этой точке существует производная f `(x), то она равна нулю:
f `(x) = 0.

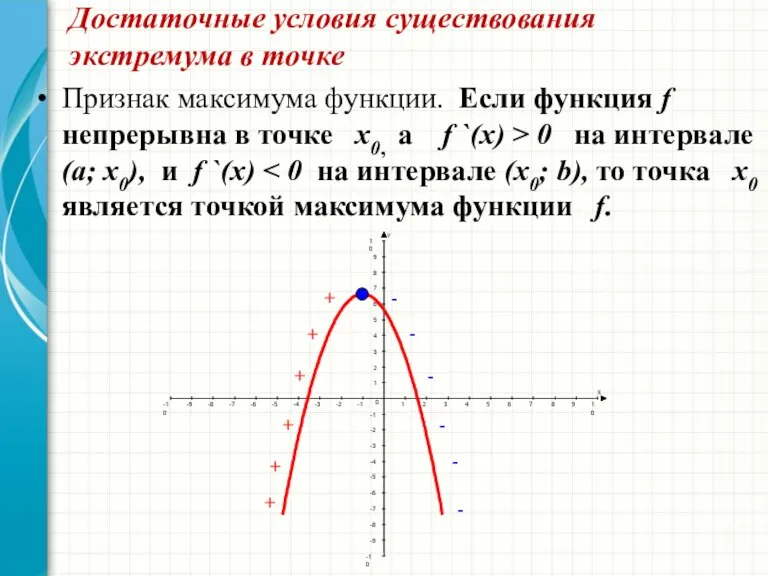
Достаточные условия существования экстремума в точке
Признак максимума функции. Если функция f непрерывна в точке х0, а f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.

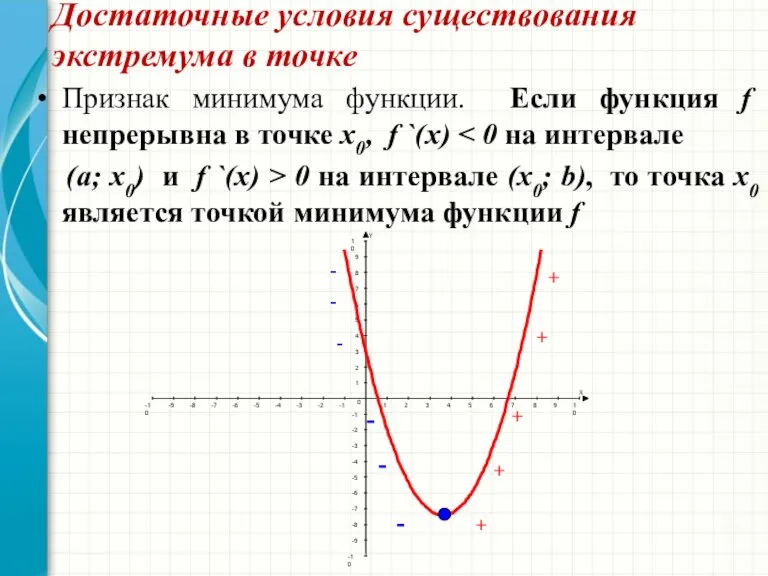
Достаточные условия существования экстремума в точке
Признак минимума функции. Если функция f непрерывна в точке х0, f `(x) < 0 на интервале
(а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f
X
Y
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
0

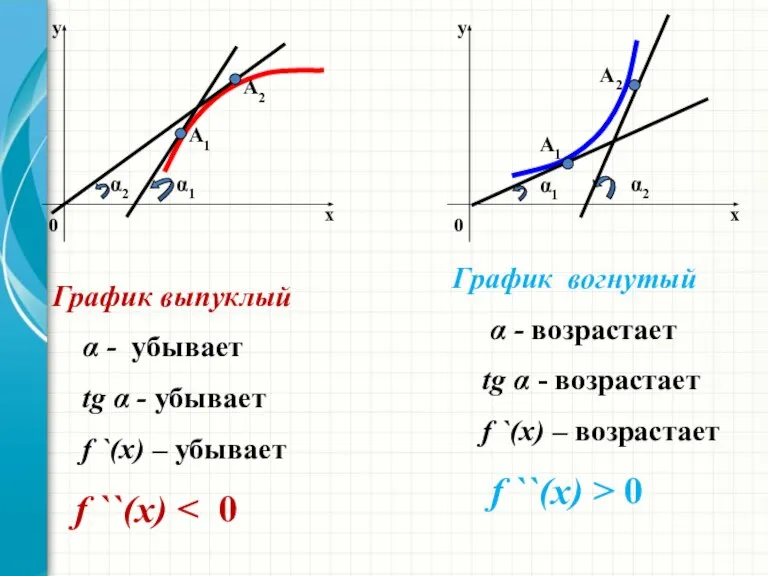
Достаточные условия выпуклости и вогнутости графика функции
Т е о р е м а. Пусть функция f(x), х(а;b), имеет первую и вторую производные. Тогда, если f ``(x) < 0 для всех х(а;b), то на интервале (а;b) график функции f(x) выпуклый вверх, если же f ``(x) > 0 для всех х(а;b), то график функции f(x) выпуклый вниз на (а;b).

1
2
График выпуклый
 - убывает
tg  - убывает
f `(x) – убывает
f ``(x) < 0
График вогнутый
 - возрастает
tg  - возрастает
f `(x) – возрастает
f ``(x) > 0
1
2
A1
A2
A1
A2