Способы задания функций

Способы:
Путем параллельного переноса вдоль оси ординат
Путем растяжения вдоль ОY
Параллельным переносом вдоль оси абсцисс
Путем растяжения вдоль оси Х с коэффициентом K

1)
Параллельный перенос на вектор с координатами (0; b) вдоль оси ординат который будет задаваться формулой (х;f (х)) → (х;f (х)+b)
Для построения графика (х;f (х)+b), где b – постоянное число, надо перенести график f на вектор (0; b) вдоль оси ординат

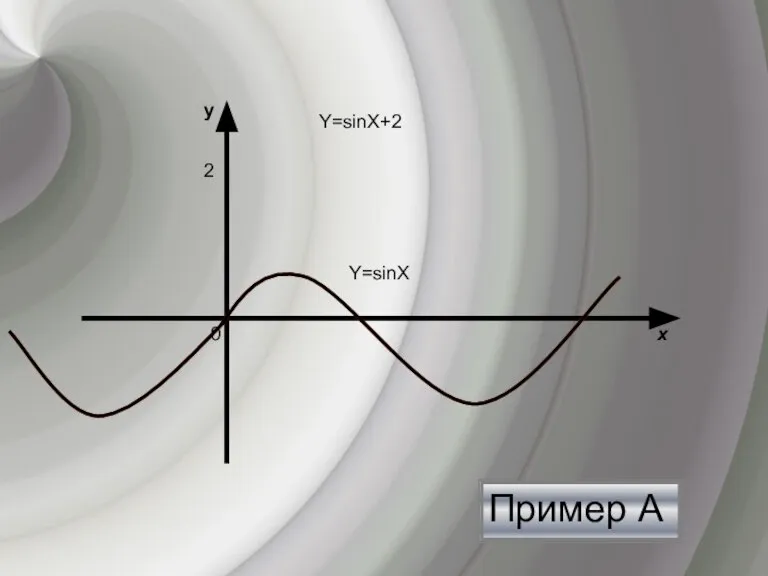
y
х
0
Y=sinХ+2
Y=sinХ
2
Пример А

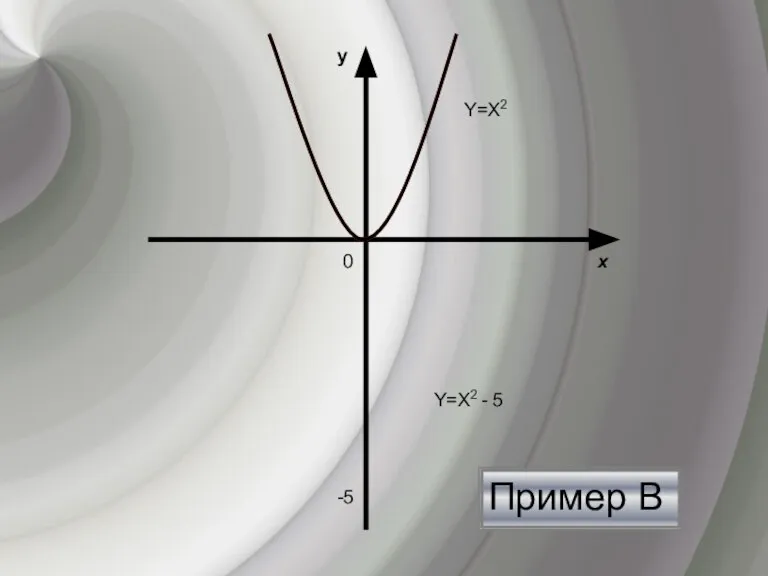
х
y
0
-5
Y=Х2
Y=Х2 - 5
Пример В

Растяжение вдоль оси ОY с коэффициентом K, который задается формулами Х`=Х; Y`=KY
( х;f (х)) → ( х;f к(х) )
Для построения y= кf(х) надо растянуть график функции y= f(х) в к раз вдоль оси ординат
2)

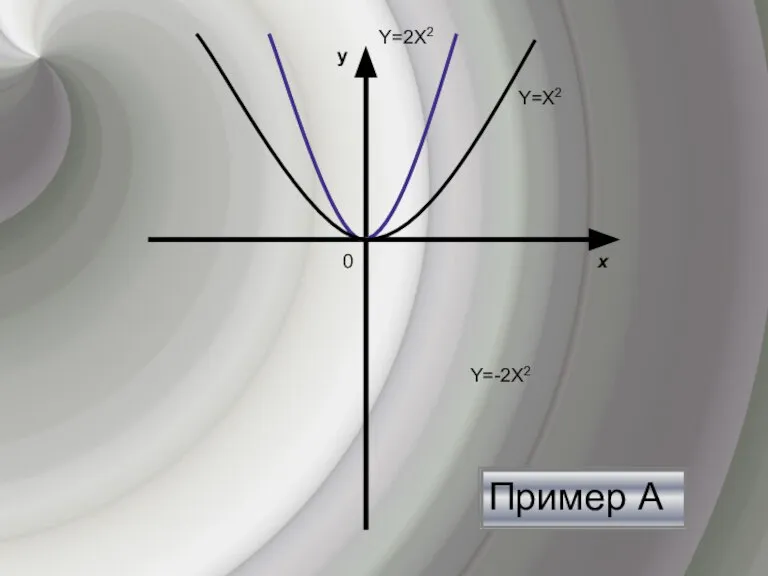
Пример А
х
y
0
Y=Х2
Y=-2Х2
Y=2Х2

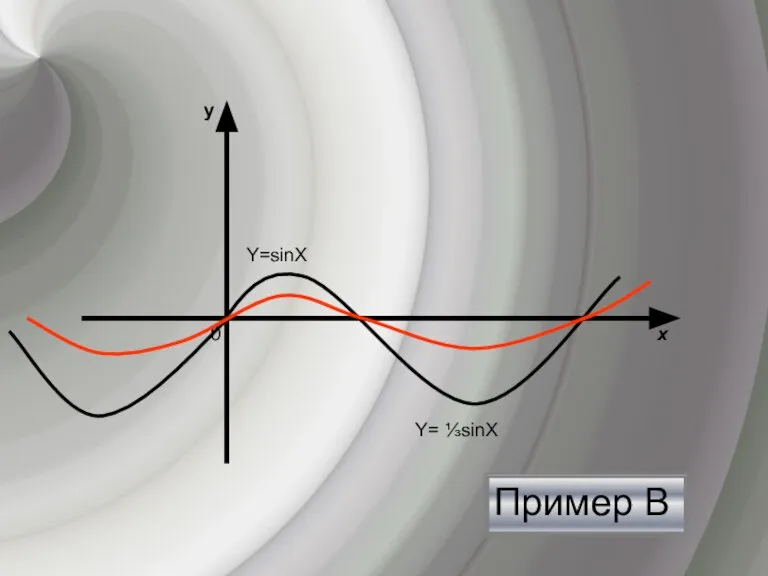
Пример В
Пример В
y
х
0
Y= ⅓sinХ
Y=sinХ

Параллельный перенос вдоль оси абсцисс на вектор с координатами (a;0) с формулами Х`=Х; Y`=KY
(х+a;f (х)) → (х;f (х)+a)
График y=f (х)-a получается путем переноса вдоль оси абсцисс на вектор (a;0), если a>0, то вектор направлен в противоположную сторону, a<0- отрицательную
3)

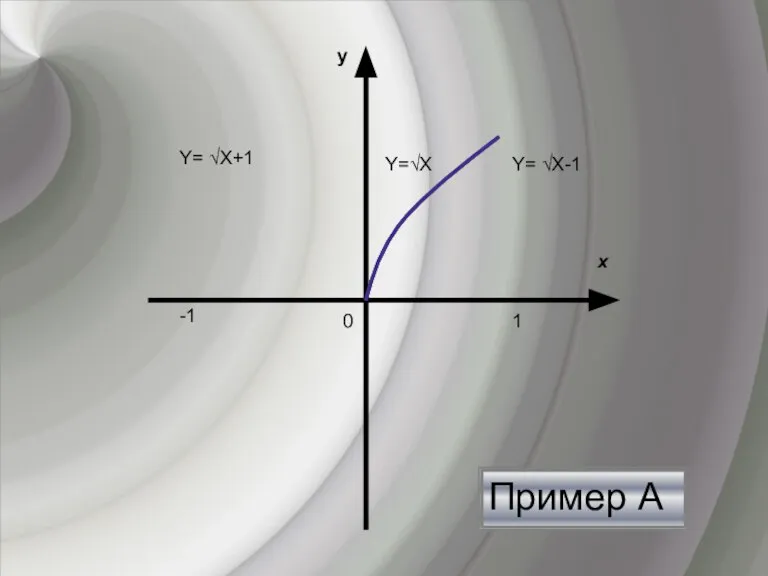
Пример А
х
y
0
Y=√Х
Y= √Х-1
Y= √Х+1
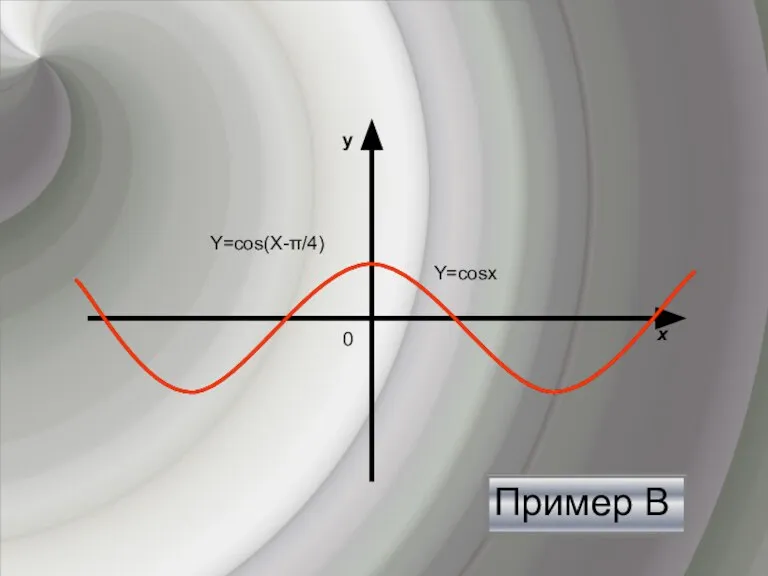
-1
1

Пример В
y
х
0
Y=cosх
Y=cos(Х-π/4)

Растяжение вдоль оси х с коэффициентом K задается формулами
Х`=KХ; Y`=Y
(х;f (х)) → (х;f (х)/k)
Для построения y= f(х)/k) надо подвергнуть график растяжению с коэффициентом k вдоль оси абсцисс
4)

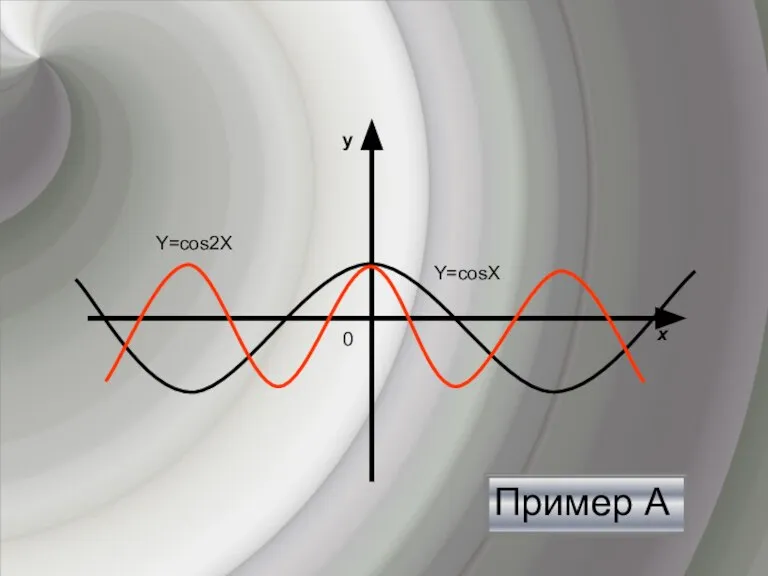
Пример А
y
х
0
Y=cosХ
Y=cos2Х

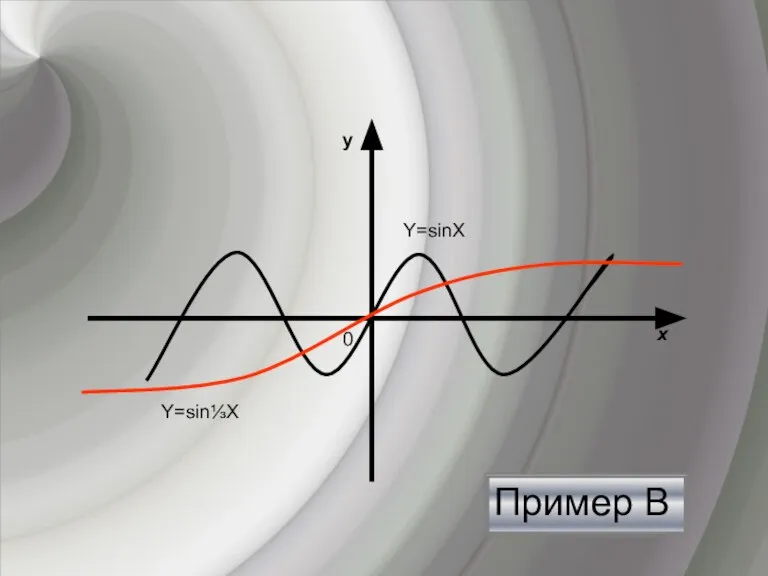
Пример В
y
х
0
Y=sinХ
Y=sin⅓Х