Решение квадратных уравнений Выполнили учителя Мкоу гимназии вятские поляны: Гатауллина гульфия анасовна и малькова надежда

Какое уравнение называется квадратным?
Формула для вычисления дискриминанта.
Формулы для нахождения корней.
Определение неполного квадратного уравнения.
Решение неполных квадратных уравнений.
Теорема Виета .
Корни квадратного уравнения для чётного b.
Особые случаи.
Проверь себя.
Старинная индийская задача

Определение:
Квадратное уравнение — это уравнение вида
aх2+ bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Квадратные уравнения можно условно разделить на три класса:
Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

Дискриминант
D = b2− 4ac.
Если D < 0, корней нет;
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

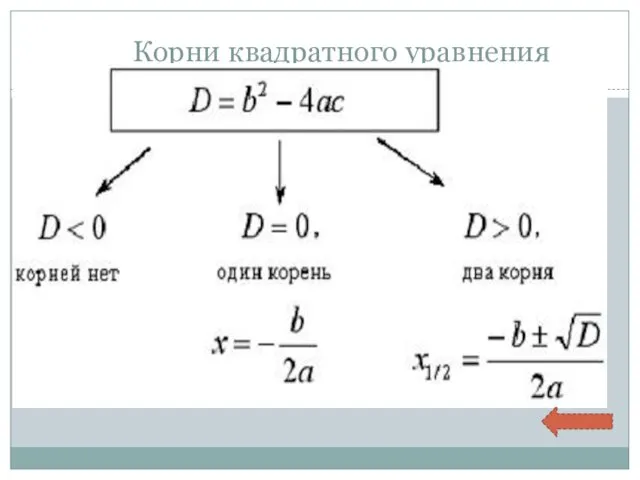
Корни квадратного уравнения

Неполные квадратные уравнения
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Решение неполных квадратных уравнений

Теорема Виета
ax2+bx+c=0
Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

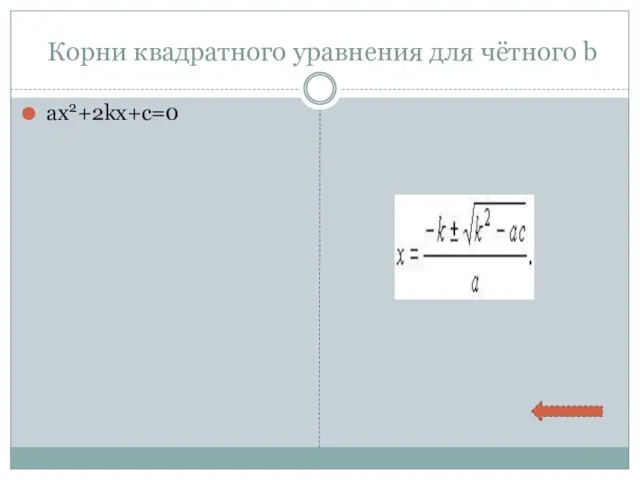
Корни квадратного уравнения для чётного b
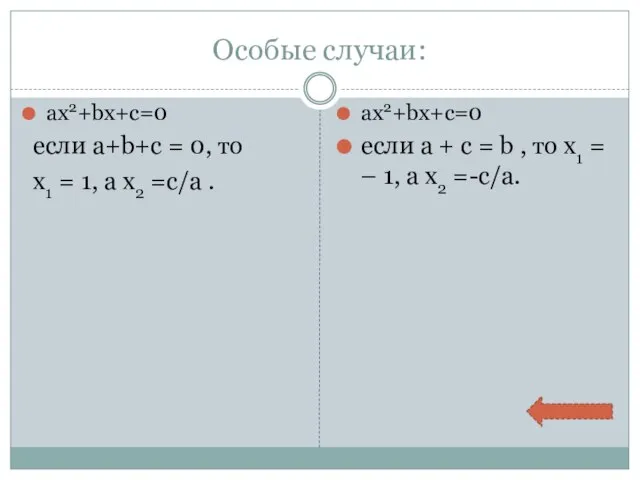
ax2+2kx+c=0

Особые случаи:
ax2+bx+c=0
если a+b+c = 0, то
х1 = 1, а х2 =c/a .
ax2+bx+c=0
если a + c = b , то х1 = – 1, а х2 =-c/a.

Сколько корней имеют квадратные уравнения:
x2 − 8x + 12 = 0;
5x2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.

Решение
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Ответ1) 2 корня; 2) нет корней; 3) один корень.

Решить квадратные уравнения:
а)x2 − 2x − 3 = 0;
б)15 − 2x − x2 = 0;
в) x2 + 12x + 36 = 0.

Решение

Решение:

Решение:

Решить неполные квадратные уравнения:
а)x2 − 7x = 0;
б)5x2 + 30 = 0;
в)4x2 − 9 = 0.

Решение:
а)x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0;
x2 = −(−7)/1 = 7.
б)5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
в)4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Ответ: а) x1 = 0; x2 = 7;
б) корней нет;
в) x1 = 1,5; x2 = 1,5.

Решите уравнения
2х²-5х+3=0 4х²+7х+3=0
3х²+4х-7=0 2х²-5х-7=0
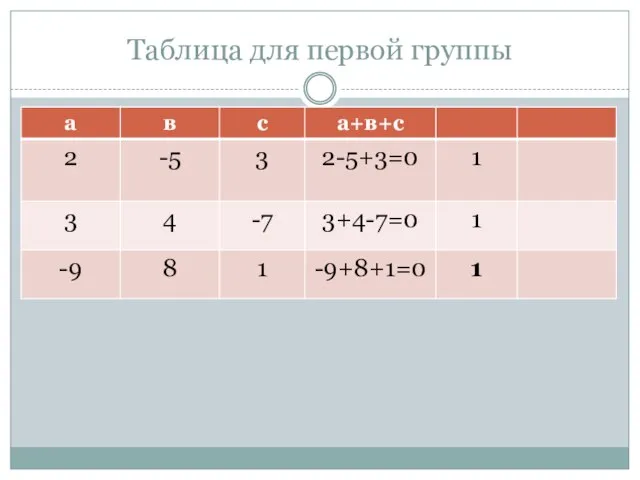
-9х²+8х+1=0 -3х²+5х+8=0

Таблица для первой группы

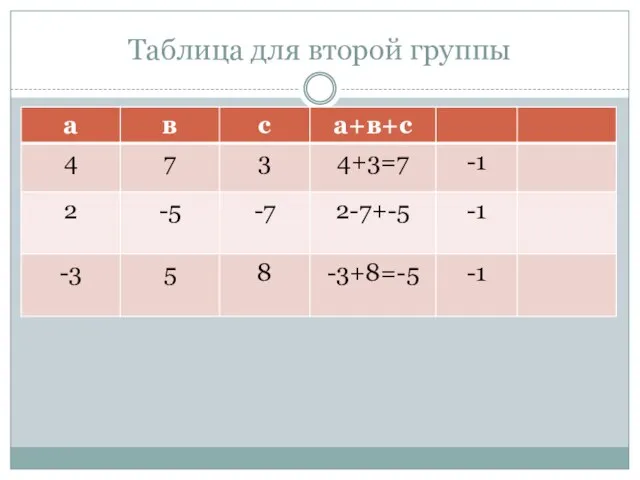
Таблица для второй группы

Одна из задач знаменитого индийского математика XІІ века Бхаскары
Обезьянок резвых стая Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать повисая…
Сколько было обезьянок
Ты скажи мне, в этой стае?.

Решение задачи Бхаскары