Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко

Цели:
развитие логического мышления формируя умения и навыки решения систем и совокупностей неравенств, выполняя равносильные переходы;
развитие умения кратко отвечать на вопрос и ставить его;
развитие учебно-коммуникативных умений при работе в группе (слушать, аргументировать, доходчиво объяснять);
развитие умений работать во времени;
развитие навыков самостоятельной деятельности и самоконтроля.

Определение
Таким образом, два неравенства являются равносильными на множестве Х, если множества решений этих неравенств совпадают.
Два неравенства f₁(х)>g₁(х) и f₂(х)
б) или оба неравенства не имеют решений.

Поэтому вместо того чтобы решать данное неравенство, можно решать любое другое, равносильное данному.
Замену одного неравенства другим, равносильным данному на Х, называют равносильным переходом на Х.
Равносильный переход обозначат двойной стрелкой
Например: х²<1 |х|<1.

Важно понимать, что для доказательства неравносильности двух неравенств нет необходимости решать каждое из неравенств, а затем убеждаться в том, что множества их решений не совпадают – достаточно указать одно решение одного из неравенств, которое не является решением другого неравенства.

Пусть функции f(x), g(x), h(x) определены на множестве Х. Тогда справедливы следующие равносильные переходы:

Системы и совокупности неравенств
Определение.
Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все такие значения переменной, каждое из которых является частным решением заданных неравенств.
Частное решение системы неравенств – значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.
Множество всех частных решений системы неравенств представляют собой общее решение системы неравенств.

Решить систему неравенств – значит найти все её частные решения.
Решение системы неравенств представляет собой пересечение решений неравенств, образующих систему.
Неравенства, образующие систему, объединяются фигурной скобкой.

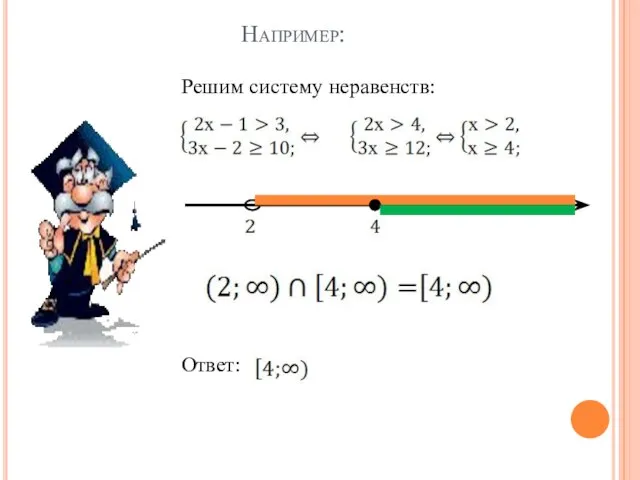
Например:
Решим систему неравенств:
Ответ:

Определение.
Несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие значения переменной, каждое из которых является хотя бы одного из заданных неравенств.
Каждое такое значение переменной называют частным решением совокупности неравенств.
Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств.

Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность.
Неравенства, образующие совокупность, объединяются квадратной скобкой.

Например
Решим совокупность неравенств
Ответ:

Задание группам
№ 57.4а;
№ 57.5а;
№ 57.8а.

Домашнее задание
№№
57.4б,
57.5б,
57.8б.

Самостоятельная работа
1 вариант
№№
57.6а,
57.7а,
57.9а.
2 вариант
№№
57.6б,
57.7б,
57.9б.