ГИА 2013 Модуль «АЛГЕБРА» №2

Модуль «Алгебра» №2
Повторение (2)
На координатной прямой отмечено число а.
Из следующих неравенств выберите верное:
Ответ: 3
Исходя из рисунка 5<а<6,
а – 6 > 0
4 – а > 0
5 – а < 0
а – 3 < 0
⇒
а – 6 < 0
4 – а < 0
5 – а < 0
а – 3 > 0

Повторение (подсказка)
Если из меньшего числа вычесть большее, то результат будет отрицательный.
Если из большего числа вычесть меньшее, то результат будет положительный.

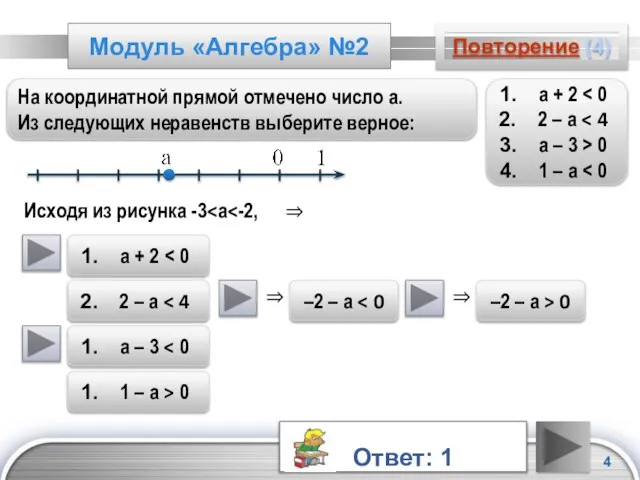
Модуль «Алгебра» №2
Повторение (4)
На координатной прямой отмечено число а.
Из следующих неравенств выберите верное:
Ответ: 1
Исходя из рисунка -3<а<-2,
а + 2 < 0
2 – а < 4
а – 3 > 0
1 – а < 0
⇒
а + 2 < 0
2 – а < 4
а – 3 < 0
1 – а > 0
⇒
–2 – а < 0
⇒
–2 – а > 0

Повторение (подсказка)
Чтобы сложить числа с разными знаками, надо из большего модуля вычесть меньший, и поставить знак числа с большим модулем.
При решении неравенств можно переносить слагаемые из одной части в другую, меняя знак слагаемых на противоположный.
Чтобы вычесть из одного числа другое, надо к первому числу прибавить чило противоположное второму.
Чтобы сложить два отрицательных числа, надо сложить их модули, а перед полученным ответом поставить знак «минус».

Модуль «Алгебра» №2
Повторение (2)
На координатной прямой отмечено число а.
Из следующих неравенств выберите верное:
Ответ: 3
Числа -5 и 5 находятся на одном и том же расстоянии от числа а,
след. число а=0.
а < 0
а² > 0
а² – 1 < 0
а > 0
⇒
а = 0
а² = 0
а² – 1 < 0
а = 0

Повторение (подсказка)
Квадрат нуля равен нулю.
Если из нуля вычесть положительное число, то результат будет отрицательный.

Модуль «Алгебра» №2
Повторение (2)
На координатной прямой отмечено число а.
Из следующих неравенств выберите верное:
Ответ: 4
Исходя из рисунка 2<а<3,
а² < 4
(а – 2)² > 1
(а – 3)² > 1
а² < 9
⇒
а² > 4
(а – 2)² < 1
(а – 3)² < 1
а² < 9
Так как 4 = 2²
Так как а – 2 < 1
Так как –1<(а – 3)<0
Так как а < 3, а 9=3²

Повторение (подсказка)
Если 0<а<1, то а – правильная дробь. Квадрат правильной дроби есть правильная дробь, т.е. меньше единицы.
Если -1<а<0, то а – отрицательная правильная дробь. Квадрат отрицательного числа есть число положительное.

Модуль «Алгебра» №2
Повторение (3)
Найдите координату точки А.
Ответ: 1)-5; 2)-21; 3)1,75
.
.
.
1.Так как точка А находится левее нуля на 5 единичных отрезков, то ее координата равна -5.
2.Так как между числами -3 и -45 семь делений, то цена деления равна 6. Т.е. (-3-(-45)):7=6
А т. к. точка А правее числа -45 на четыре деления, то –45+6∙4=–21
3.Так как точка А находится правее нуля, то ее координата «+».
Так как единичный отрезок имеет четыре деления, то цена деления равна 1:4=0,25.
Так как от единицы до числа А три деления, то А имеет координату 1+0,25∙3=1,75

Повторение (подсказка)
На координатной (числовой) прямой числа, которые лежат левее нуля, называются отрицательными.
На координатной (числовой) прямой ценой деления называется длина каждого деления в единичных отрезках.
На координатной (числовой) прямой числа, которые лежат правее нуля, называются положительными.

Модуль «Алгебра» №2
Повторение (3)
На координатной прямой отмечено числа а и b.
Из следующих неравенств выберите неверное:
Ответ: 4
Исходя из рисунка:
а < b
.
–а > –b
.
а < b
.
–а > –b
Так как b правее а.
Так как
Так как а < b.

Повторение (подсказка)
На координатной (числовой) прямой число, которое находится правее, имеет большую координату. По одному из свойств неравенств: если а
По одному из свойств неравенств: если а
–b

Модуль «Алгебра» №2
Повторение (5)
На координатной прямой отмечено числа а, b и с.
Из следующих неравенств выберите неверное:
Ответ: 3
Исходя из рисунка: c
0
аbc > 0
b² > c²
.
a+c < b
аbc > 0
b² < c²
.
Так как ас>0 и b>0.
Так как |b|<|c|
Так как
a+c < b
Так как а+с<0, b>0.

Повторение (подсказка)
Произведение двух отрицательных чисел дает положительный результат.
Чем число на координатной (числовой) прямой дальше от нуля, тем больше его модуль.
Частное двух отрицательных чисел дает положительный результат.
Сумма двух отрицательных чисел дает отрицательный результат.
Любое отрицательное число меньше любого положительного числа.

Модуль «Алгебра» №2
Повторение (3)
На координатной прямой отмечено число а. Расположите в порядке возрастания числа а-1; ; а.
Ответ: 4
Исходя из рисунка a>0, a<1.
.
.
.
.
а -1 < 0
Так как а левее единицы.
Так как а – правильная дробь
Так как неправильная дробь больше единицы

Повторение (подсказка)
Если из меньшего числа вычесть большее, то получится отрицательное число.
Числа а и - взаимно обратные числа.
Если данное число – правильная дробь, то ему взаимно обратное число – неправильная дробь.

Модуль «Алгебра» №2
Повторение (4)
На координатной прямой отмечено число а. Расположите в порядке убывания числа а; -а; а².
Ответ: 2
Исходя из рисунка a<0, |a|<1.
-а; а; а².
-а; а²; а.
а²; -а; а.
а; а²; -а.
-a > 0
а²>0
Так как |a|<1, то а – дробь правильная
|а²|<|а|

Повторение (подсказка)
а и –а – противоположные числа.
Если данное число положительное, то противоположное ему число - отрицательное.
Квадрат любого числа есть число неотрицательное.
Если число умножить на правильную дробь, то оно уменьшается.

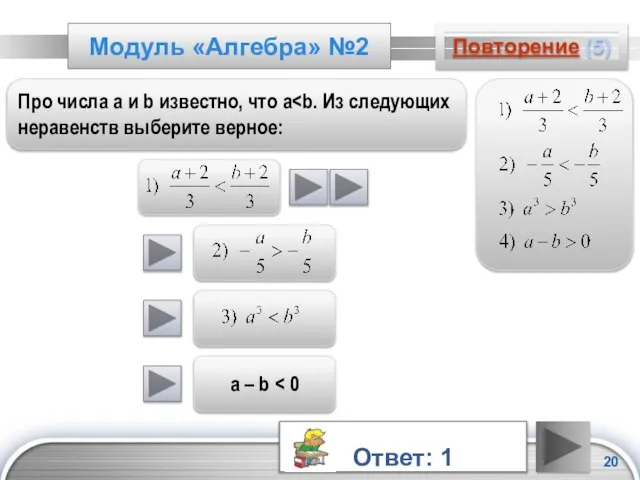
Модуль «Алгебра» №2
Повторение (5)
Про числа а и b известно, что a следующих неравенств выберите верное:
Ответ: 1
a – b < 0

Повторение (подсказка)
Если к обеим частям неравенства прибавить одно и то же число, то получим равносильное неравенство.
Если обе части неравенства разделить на одно и то же положительное число, то получим равносильное неравенство, при этом знак неравенства не изменится.
Если обе части неравенства разделить на одно и то же отрицательное число, при этом изменить знак неравенства то получим равносильное неравенство.
Нечетная степень числа сохраняет его знак.
Если из меньшего числа вычесть большее, то получится отрицательное число.

Модуль «Алгебра» №2
Повторение (6)
Про числа а и b известно, что a<0 следующих неравенств выберите неверное:
Ответ: 1
Так как a<0, b>0.
⇒
Так как a<0, b>0.

Повторение (подсказка)
Произведение двух чисел с разными знаками дает отрицательный результат.
По свойству транзитивности, если a<0
Если обе части неравенства умножить или разделить на -1, то знак неравенства изменится на противоположный..
Если a < b, то .
Если обе части неравенства разделить или умножить на положительное число, то получим равносильное неравенство, при этом знак неравенства не меняется.
Частное двух чисел с разными знаками дает отрицательный результат.

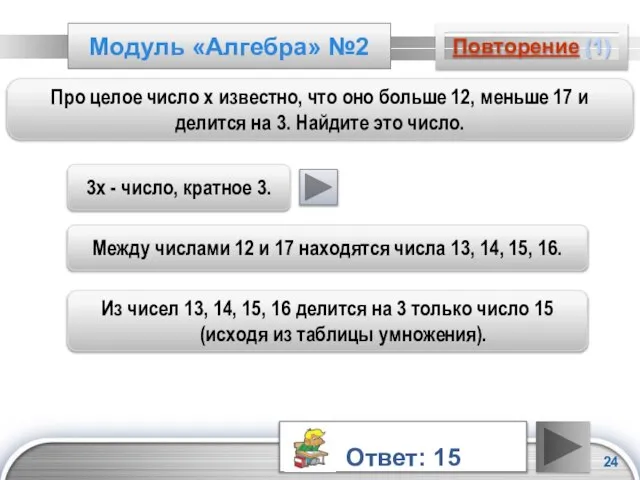
Модуль «Алгебра» №2
Повторение (1)
Про целое число х известно, что оно больше 12, меньше 17 и делится на 3. Найдите это число.
Ответ: 15
3х - число, кратное 3.
Между числами 12 и 17 находятся числа 13, 14, 15, 16.
Из чисел 13, 14, 15, 16 делится на 3 только число 15 (исходя из таблицы умножения).

Повторение (подсказка)
Числа, кратные 3 - это числа, которые делятся на 3.

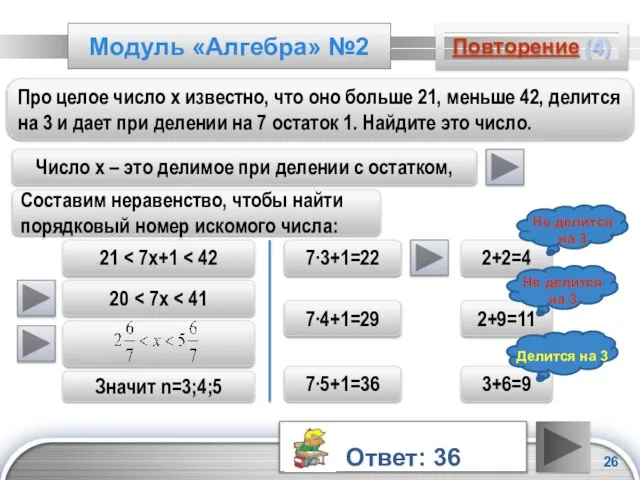
Модуль «Алгебра» №2
Повторение (4)
Про целое число х известно, что оно больше 21, меньше 42, делится на 3 и дает при делении на 7 остаток 1. Найдите это число.
Ответ: 36
Число х – это делимое при делении с остатком,
Составим неравенство, чтобы найти
порядковый номер искомого числа:
20 < 7x < 41
Значит n=3;4;5
21 < 7x+1 < 42
7∙3+1=22
2+2=4
Не делится на 3
7∙4+1=29
2+9=11
Не делится на 3
7∙5+1=36
3+6=9
Делится на 3

Повторение (подсказка)
Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.
При решении неравенств можно прибавлять ко всем частям неравенства одно и то же число, знак неравенства при этом не меняется.
Если при решении неравенств разделить все части неравенства одно и то же положительное число, знак неравенства при этом не меняется.
Признак делимости на 3 говорит: если сумма цифр числа делится на 3, то и число делится на 3.