Логарифм числа

Изобретение логарифмов,
сократив работу астронома, продлило ему жизнь.
П.С. Лаплас

Введение понятия логарифма числа;
Знакомство с основным логарифмическим тождеством;
Научить применять определение логарифма и тождества к вычислениям и решению простейших логарифмических уравнений.
Цели и задачи урока:

X—показатель степени
имеет единственный корень

x

Определение
Логарифмом числа b, по
основанию а, где b>0, a>0,а≠1, называется показатель степени, в которую надо возвести а, чтобы получить число b.

Из определения логарифма
следует:
Основное логарифмическое тождество

Из определения следует:

Взаимно обратные действия:
Возведение в
степень
Логарифмирование

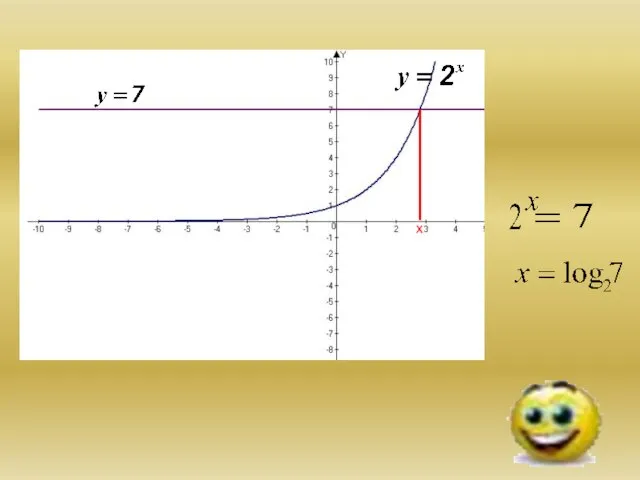
Решить
уравнение:
По определению
логарифма:
При каких х
существует
?
Т.К. 5>1 и 5=1, то данный логарифм существует при условии, что
1
2
х
+
-
+