Элементы математической статиститки

Статистика – дизайн информации

Цель:
Дать понятие генеральной и выборочной совокупности, полигону и гистограмме частот
Научиться строить полигон и гистограмму частот
Познакомится с параметры оценки генеральной совокупности

Генеральная совокупность и выборка
Опр 1: Генеральной совокупностью называется совокупность, из которой отбирают часть объектов.
Опр 2: Выборка (или выборочная совокупность) - это множество объектов, случайно отобранных из генеральной совокупности.
Опр 3: Число объектов генеральной совокупности и выборки называют соответственно объемом генеральной совокупности и объемом выборки.

Опр 4: Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной.

Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем x1, x2, … xk объёма N.
Опр 5: Наблюдаемые значения x1, x2, … xk называют вариантами, а последовательность вариант, записанная в возрастающем порядке, - вариационным рядом.
Опр 6: Числа наблюдений n1, n2, …nk называют частотами, а их отношения к объему
, , …,
- относительными частотами.
Сумма относительных частот равна единице:

Опр 7: Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

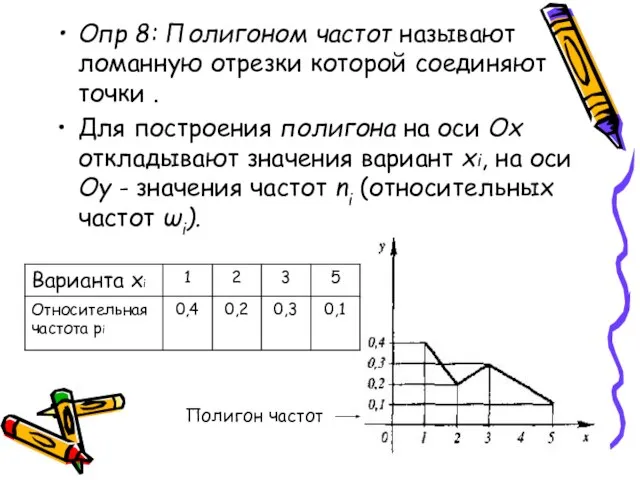
Опр 8: Полигоном частот называют ломанную отрезки которой соединяют точки .
Для построения полигона на оси Ох откладывают значения вариант xi, на оси Оу - значения частот ni (относительных частот ωi).
Полигон частот

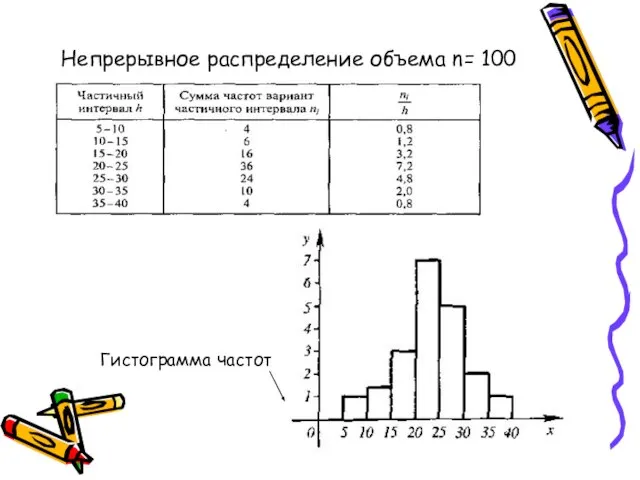
Опр 9: Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению (плотность частоты).

Непрерывное распределение объема n= 100
Гистограмма частот

Оценка параметров генеральной совокупности
Опр 10: Статистической оценкой Θ* неизвестного параметра Θ теоретического распределения называют функцию от наблюдаемых случайных величин .
Опр 11: Точечной называют статистическую оценку, которая определяется одним числом
, где -
результаты n наблюдений над количественным признаком X (выборка).

Опр 12: Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Опр 13: Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.

Опр 14: Выборочной средней называют среднее арифметическое значений признака выборочной совокупности.
Опр 15: Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочного среднего .

Несмещенной оценкой генеральной средней (математического ожидания)
служит выборочная средняя ,
где xi – варианта выборки, ni – частота варианты xi ,
- объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
или .
Смещенной оценкой генеральной дисперсии служит выборочная
дисперсия

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии .

Доверительный интервал – это интервал, который с заданной вероятностью покрывает неизвестную характеристику.

Доверительный интервал для математического ожидания
где - аргумент распределения Стьюдента, соответствующей доверительной вероятности γ и (N-1) степени свободы.

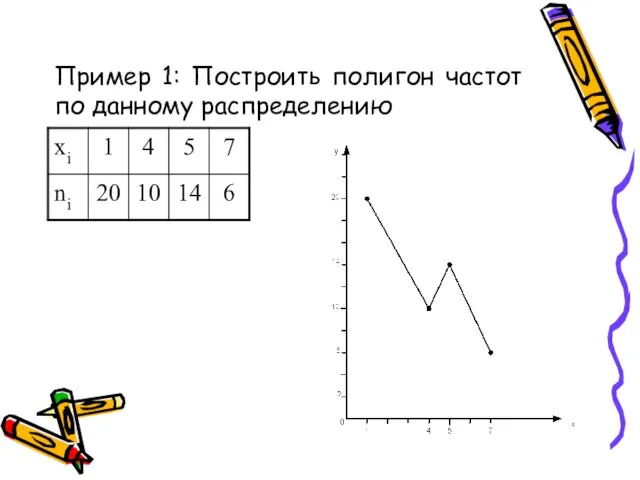
Пример 1: Построить полигон частот по данному распределению

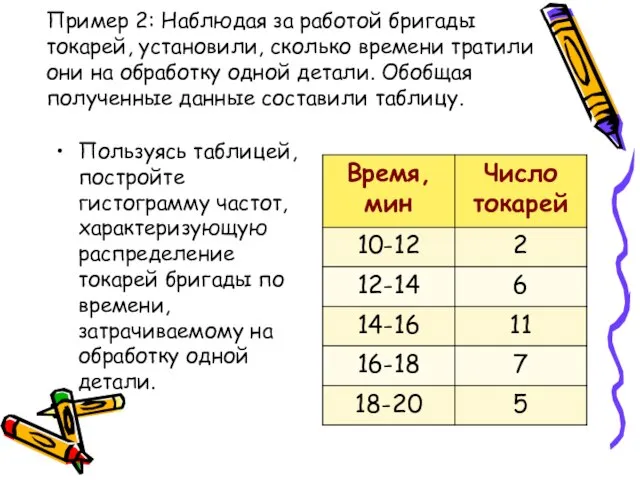
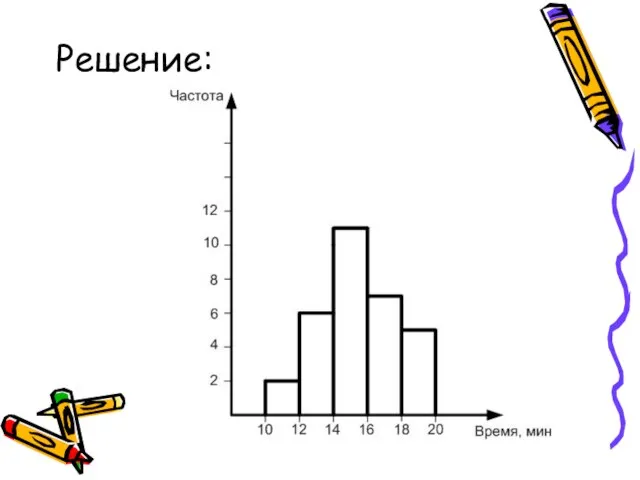
Пример 2: Наблюдая за работой бригады токарей, установили, сколько времени тратили они на обработку одной детали. Обобщая полученные данные составили таблицу.
Пользуясь таблицей, постройте гистограмму частот, характеризующую распределение токарей бригады по времени, затрачиваемому на обработку одной детали.

Решение:

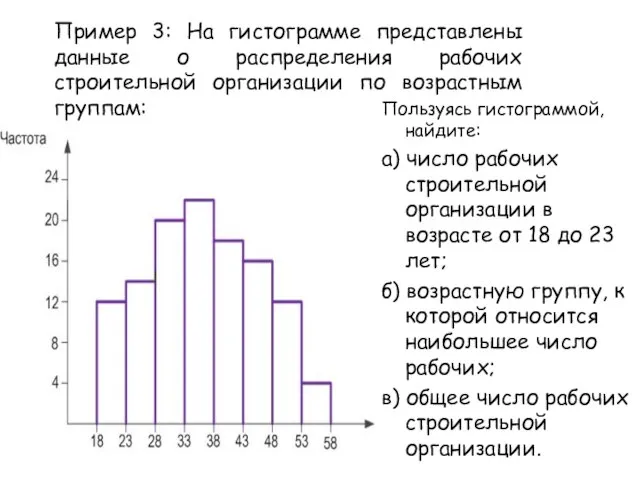
Пример 3: На гистограмме представлены данные о распределения рабочих строительной организации по возрастным группам:
Пользуясь гистограммой, найдите:
а) число рабочих строительной организации в возрасте от 18 до 23 лет;
б) возрастную группу, к которой относится наибольшее число рабочих;
в) общее число рабочих строительной организации.