Содержание
- 2. Статистические характеристики Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых
- 3. Статистические характеристики Среднее арифметическое. Размах. Мода.
- 4. СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ При изучении учебной нагрузки учащихся выделили группу из 10 семиклассников. Их попросили отметить в
- 5. Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания
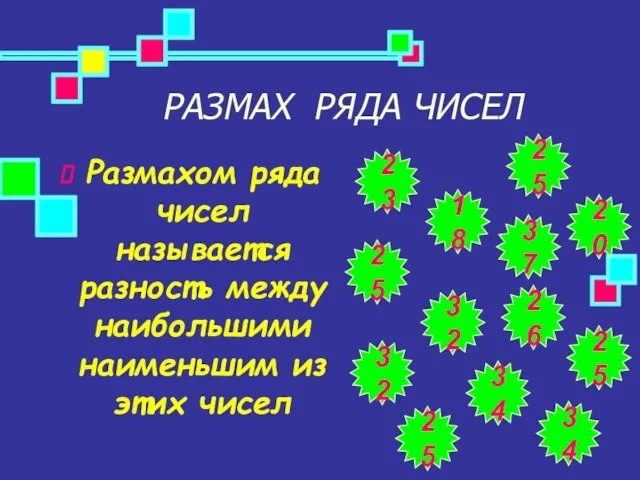
- 6. РАЗМАХ РЯДА ЧИСЕЛ Размахом ряда чисел называется разность между наибольшими наименьшим из этих чисел 26 34
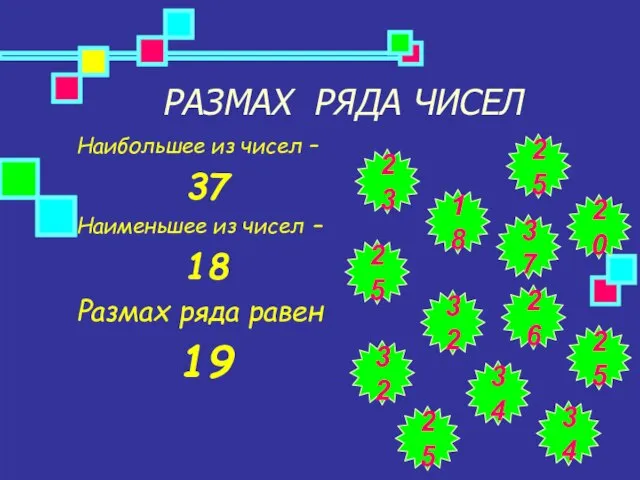
- 7. РАЗМАХ РЯДА ЧИСЕЛ Наибольшее из чисел – 37 Наименьшее из чисел – 18 Размах ряда равен
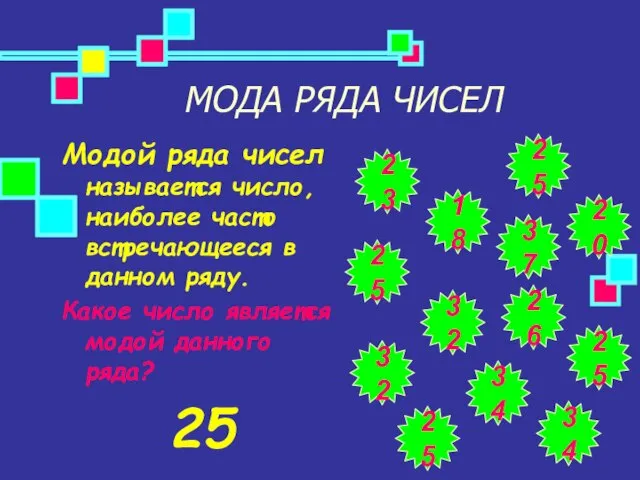
- 8. МОДА РЯДА ЧИСЕЛ Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду. Какое число
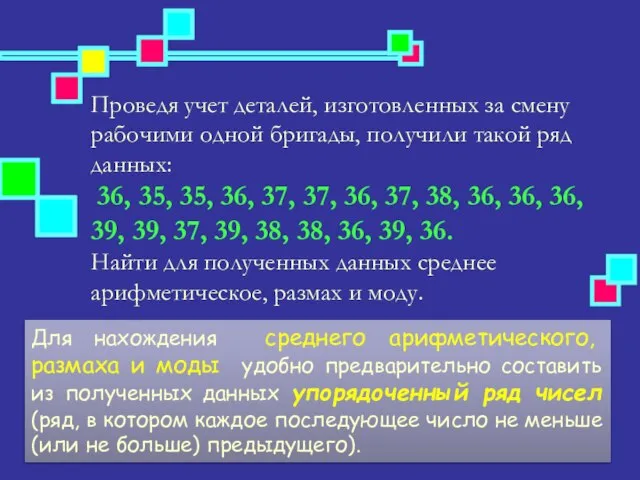
- 9. Для нахождения среднего арифметического, размаха и моды удобно предварительно составить из полученных данных упорядоченный ряд чисел
- 11. Скачать презентацию



 Степень и её свойства 7 класс
Степень и её свойства 7 класс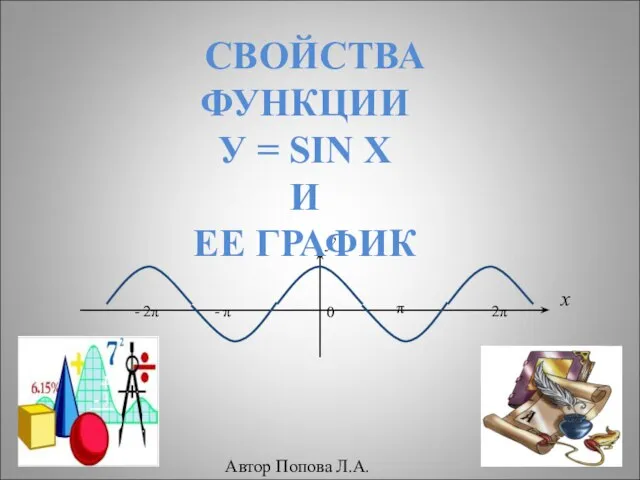 Svoystva-funkcii-ysinx-i-ee-grafik.ppt
Svoystva-funkcii-ysinx-i-ee-grafik.ppt ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Общие положения исследования неподлинной подписи
ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Общие положения исследования неподлинной подписи Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Неполные квадратные уравнения
Неполные квадратные уравнения Презентация на тему Основные теории местного самоуправления
Презентация на тему Основные теории местного самоуправления  Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»
Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»  Сумма «n» членов Арифметической прогрессии
Сумма «n» членов Арифметической прогрессии Презентация на тему Классические типы коллизионных привязок
Презентация на тему Классические типы коллизионных привязок  Презентация на тему Собор святой Софии в Константинополе
Презентация на тему Собор святой Софии в Константинополе  Логарифмические неравенства
Логарифмические неравенства Уравнения с параметрами
Уравнения с параметрами Презентация на тему Человек, индивид, индивидуальность, личность. Проблема личности в философии
Презентация на тему Человек, индивид, индивидуальность, личность. Проблема личности в философии  Презентация на тему Место муниципального права в российском праве
Презентация на тему Место муниципального права в российском праве  Что изучает алгебра
Что изучает алгебра В6 элементы теории вероятностей
В6 элементы теории вероятностей Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Построение графика квадратичной функции
Построение графика квадратичной функции Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Решение систем линейных уравнений с тремя переменными - презентация по Алгебре_
Решение систем линейных уравнений с тремя переменными - презентация по Алгебре_ Геометрическая прогрессия 9 класс
Геометрическая прогрессия 9 класс Производная степенной функции. Ее геометрический смысл
Производная степенной функции. Ее геометрический смысл Презентация на тему ОЩУЩЕНИЯ
Презентация на тему ОЩУЩЕНИЯ  Презентация на тему Как связаны неживая и живая природа
Презентация на тему Как связаны неживая и живая природа  Функция y = k√x . Подкоренная функция
Функция y = k√x . Подкоренная функция МБОУ «чульская основная общеобразовательная школа» Учитель Генералова О.В. Определение степени с натуральным показателем 7
МБОУ «чульская основная общеобразовательная школа» Учитель Генералова О.В. Определение степени с натуральным показателем 7 Методы решения уравнений
Методы решения уравнений