Тема урока: «Производные тригонометрических функций» Автор: учитель математики Гулова Римма Ивановна г.Старый Оскол 2011г.

Ввести формулы производных тригонометрических функций
рассмотреть методы решения упражнений на применение изученных правил дифференцирования; вырабатывать умения и навыки учащихся в решении заданий на применение знаний правил вычисления производных тригонометрических функций.
Воспитание и развитие логического мышления учащихся.
Цели урока:

1.Орг. момент.
2.Актуализация опорных знаний учащихся.
3.Изучение нового материала.
3.1.Формула производной синуса
3.2.Формулы дифференцирования косинуса, тангенса и котангенса.
4.Закрепление изученного материала:
4.1. Работа у доски и на местах. Решение упражнений из учебника .
4.2.Работа в группах.
5.Подведение итогов урока.
6.Домашнее задание.
План урока

Написать на доске чему равна производная:
числа
переменной «х»
выражения kx + b
суммы функций
произведения двух функций
частного двух выражений
степенной функции
сложной функции
Актуализация опорных знаний учащихся:

Формулы вычисления производных

1)Формула производной синуса
Докажем, что производная синуса имеет такой вид:

Вспомним определение производной:

Воспользуемся формулой суммы и разности тригонометрических функций :

Для вывода формулы производной синуса достаточно показать, что:

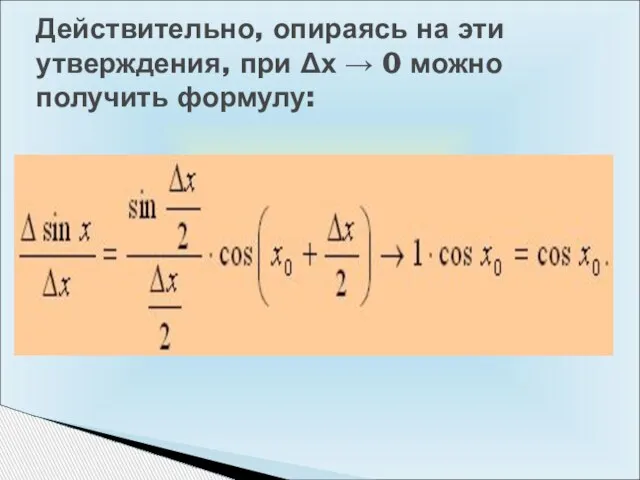
Действительно, опираясь на эти утверждения, при Δх → 0 можно получить формулу:

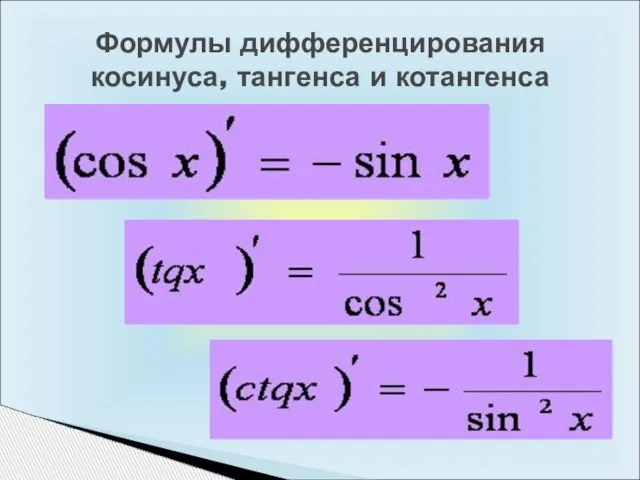
Формулы дифференцирования косинуса, тангенса и котангенса

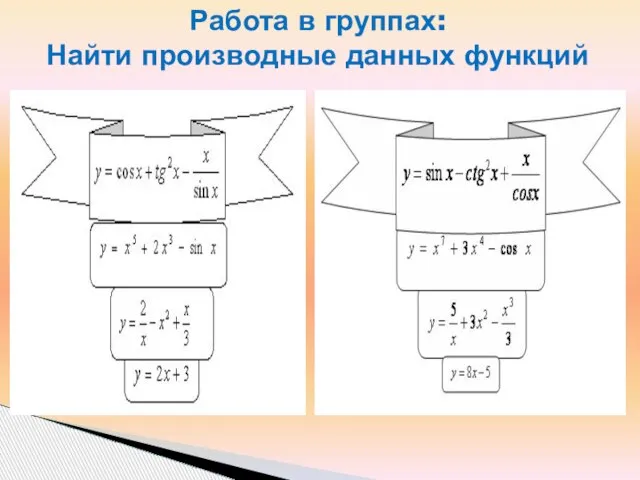
Работа в группах:
Найти производные данных функций

Что чувствовали сегодня на уроке?
С какими трудностями вы встретились?
Кому было трудно? Почему? Что ты сделал, чтобы преодолеть эту трудность?
Что тебе помогло? (Опорные конспекты, подсказки товарищей…)
Подведение итогов урока

Пункт 17 ,
№ 235, 236 (а, б).
Домашнее задание: