Свойство периодичности - презентация по Алгебре_

Периодические функции
В природе и технике часто встречаются явления, повторяющиеся по истечении некоторого промежутка времени.
Например, при вращении Земли вокруг Солнца её расстояние от солнца всё время меняется, но после полного оборота Земля оказывается на том же расстоянии от солнца, сто и год тому назад. Возвращается на своё место после полного оборота и лопасть турбины.
Такие периодические повторяющиеся процессы описываются периодическими функциями.

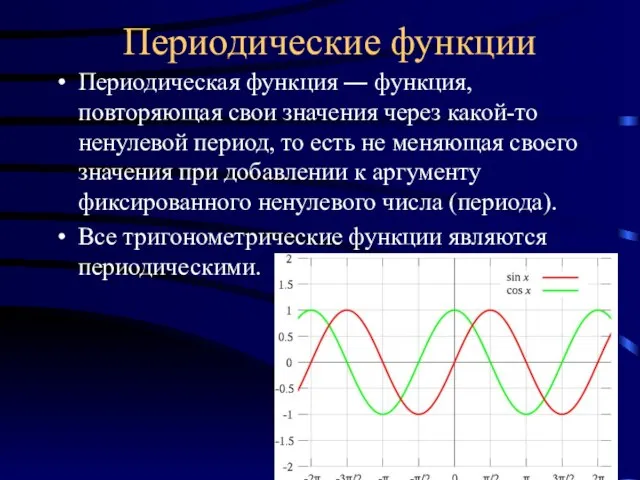
Периодические функции
Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).
Все тригонометрические функции являются периодическими.

Периодические функции
Определение 1
Говорят, что функция y=f(x), x принадлежит Х имеет период Т, если для любого x принадлежит Х выполняются равенства
f(x-T)=f(x)=f(x+T).
Из этого определения следует, что если функция с периодом Т определена в точке х, то она определена в точках х+Т ,х-Т.
Любая функция имеет период, равный нулю(при Т=0 равенство превращается в тождество
f(x-0)=f(x)=f(x+0)).

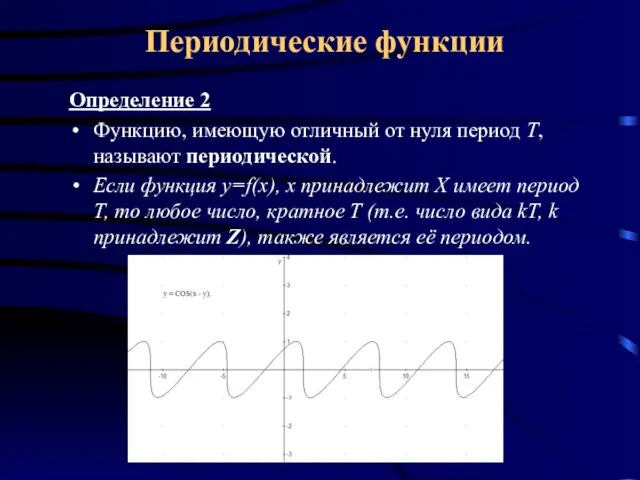
Определение 2
Функцию, имеющую отличный от нуля период Т, называют периодической.
Если функция y=f(x), x принадлежит Х имеет период Т, то любое число, кратное Т (т.е. число вида kT, k принадлежит Z), также является её периодом.
Периодические функции

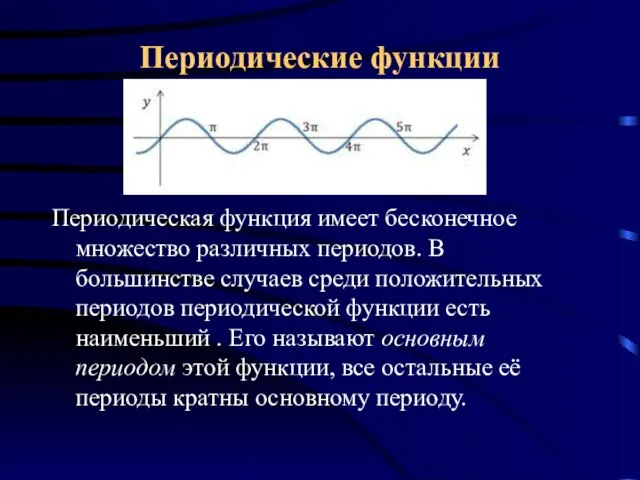
Периодические функции
Периодическая функция имеет бесконечное множество различных периодов. В большинстве случаев среди положительных периодов периодической функции есть наименьший . Его называют основным периодом этой функции, все остальные её периоды кратны основному периоду.

Периодические функции
График периодической функции обладает следующей особенностью.
Если Т - основной период функции y=f(x), то для построения её графика достаточно построить ветвь графика на одном из промежутков длины Т, а затем выполнить параллельный перенос этой ветви вдоль оси х на +Т,+2Т,+3Т, … .
Чаще всего в качестве такого промежутка длины Т выбирают промежуток с концами в точках (-Т/2;0)и(Т/2;0).

Периодические функции
Но не у всякой периодической функции есть основной период. Классический пример - функция Дирихле y=d (x), где
1,если х- рациональное число;
d (x)= 0,если х- иррациональное число.

Периодические функции
Любое рациональное число r является периодом этой функции.
В самом деле, если х-рациональное число,
то х-r, x+r –рациональные числа, а потому
d (x-r)=d (x)=d (x+r)=1.
Если же х – иррациональное число, то
х-r, х+r – иррациональные числа, а потому
d (x-r)=d (x)=d (x+r) = 0.

Периодические функции
Итак, любое рациональное число является периодом функции Дирихле.
Но среди положительных рациональных чисел нет наименьшнго числа, значит,
у периодической функции Дирихле нет основного периода.