Уравнения с параметрами

C4. Найти все значения параметра a, при каждом из которых
уравнение имеет единственное решение.
, t ≥ 0, тогда x – 8 =
; x =
+ 8 и уравнение примет вид:
Пусть
t = -a
- 8a +3a+2
a
+ t +5a – 2 = 0
Если a = 0, то уравнение имеет единственный корень
t – 2 = 0; t =2; x = 4 + 8 = 12
Если a ≠ 0 и а > 0
D= 1 – 4a(5a – 2) = 1 – 20 + 8a;
-20 + 8a + 1 > 0
20 -8a – 1 < 0

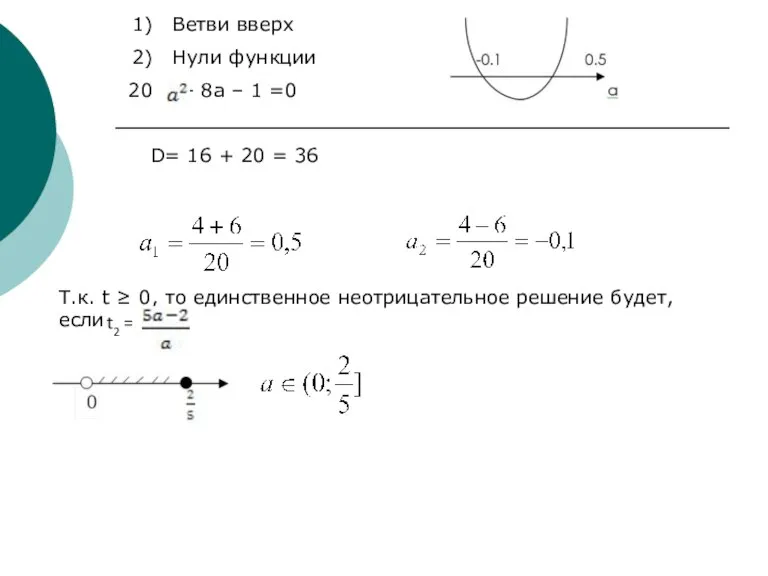
Ветви вверх
Нули функции
- 8a – 1 =0
D= 16 + 20 = 36
Т.к. t ≥ 0, то единственное неотрицательное решение будет, если
t2 =

Ответ: [0; 0,4]; -0.1
Прежде всего при решении уравнения с параметрами надо сделать то, что делается при решении любого уравнения – привести заданное уравнение к более простому виду, то есть разложить на множители, избавиться от модулей, логарифмов и т. д

Как решить задачи с параметром?
При решении задач с параметром иногда удобно, а иногда просто необходимо строить графики. Эскиз графиков иногда помогают увидеть «ход решения».
Необходимо в первую очередь рассмотреть решение при тех значениях параметра, при которых обращается в ноль коэффициент при старшей степени x, тем самым понизив степень многочлена.
C2 Найти все значения параметра a, при которых уравнение
имеет 2 различных корня.

Т.к.
, то сделаем замену переменных
и уравнение примет вид:
итак, надо найти те значения a, при которых квадратное уравнение имеет один положительный корень t
(тогда x = ±t).
Рассмотрим функцию
График функции – парабола, ветви – вверх.