Содержание
- 2. Нет повести обширнее, наверное, Чем повесть о квадратном уравнении… Определение квадратного уравнения (серия 1)
- 3. 1. Какие уравнения называют квадратными? Квадратным уравнением называют уравнение вида ax2 + bx + c =
- 4. 2. Как называются коэффициенты квадратного уравнения? а – первый или старший коэффициент, b – второй коэффициент,
- 5. 3. Какие уравнения называют приведёнными? Как из полного уравнения получить приведённое? Приведённым квадратным уравнением называют уравнение
- 6. 4. Какие бывают неполные квадратные уравнения? Если а ≠ 0, b = 0, с = 0,
- 7. 5. Описать методы решения неполных квадратных уравнений. ах2 = 0, х = 0. ах2 + bx
- 8. Решение квадратного уравнения выделением квадрата двучлена (серия 2)
- 9. 1. Запишите формулы сокращённого умножения: квадрат суммы и квадрат разности. Квадрат суммы (a + b)2 =
- 10. 2. Решите уравнения: (x + k)2 = 0 и (x – k)2 = 0. (x +
- 11. 3. Запишите алгоритм решения приведённого квадратного уравнения методом выделения квадрата двучлена. x2 + 2px + q
- 12. Формула корней квадратного уравнения (серия 3)
- 13. 1. Запишите общую формулу квадратного уравнения. ax2 + bx + c = 0, где коэффициенты a,
- 14. 2. Что такое дискриминант? D = b2 – 4ac.
- 15. 3. Какая зависимость между знаком дискриминанта и количеством решений квадратного уравнения? если D > 0, то
- 16. 4. Запишите формулу корня уравнения, если D = 0. если D = 0, то x =
- 17. 5. Запишите формулу корней уравнения, если D > 0. если D > 0, то
- 18. Теорема Виета (серия 4)
- 19. 1. Запишите формулу приведённого квадратного уравнения. x2 + px + q = 0
- 20. 2. Чему равен дискриминант приведённого квадратного уравнения? D = p2 – 4q.
- 21. 3. Сформулируйте теорему Виета для приведённого квадратного уравнения. «Сумма корней приведенного квадратного уравнения равна второму коэффициенту,
- 22. 4. Запищите формулы Виета для квадратного уравнения общего вида.
- 23. 5. Сформулируйте теорему, обратную теореме Виета. Если числа х1 и х2 таковы, что х1 + х2
- 24. Биквадратные уравнения (серия 5)
- 25. 1. Запишите общий вид биквадратного уравнения. ax4 + bx2 + c = 0
- 26. 2. Приведите алгоритм решения биквадратного уравнения. ввести новую переменную х2 = t; сделать замену в уравнении:
- 27. Домашнее задание: Пункт 3. 7. Прочитать, сделать необходимые записи в справочник.
- 29. Скачать презентацию


























 Линейное уравнение с двумя переменными и его график
Линейное уравнение с двумя переменными и его график Финансовые ресурсы государства и муниципальных образований
Финансовые ресурсы государства и муниципальных образований Применение производной к исследованию функции
Применение производной к исследованию функции Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Алгебраический тренажёр
Алгебраический тренажёр Преобразование двойных радикалов 8 класс
Преобразование двойных радикалов 8 класс Презентация на тему Экономика стран Австралии и Океании
Презентация на тему Экономика стран Австралии и Океании  Презентация на тему Блиц - Опрос
Презентация на тему Блиц - Опрос  Презентация на тему Основные положения модели управления качеством А. Фейгенбаума
Презентация на тему Основные положения модели управления качеством А. Фейгенбаума  Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Действия над обыкновенными дробями
Действия над обыкновенными дробями Алгебра и начала анализа
Алгебра и начала анализа Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Расположение точек относительно осей координат
Расположение точек относительно осей координат Возрастание и убывание функций
Возрастание и убывание функций  Движения графиков функций
Движения графиков функций Презентация на тему Анализ человеческого потенциала совета федераций
Презентация на тему Анализ человеческого потенциала совета федераций  ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи
ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи Презентация на тему Зрительные Искажения
Презентация на тему Зрительные Искажения  Решение простейших логарифмических логарифмических уравнений
Решение простейших логарифмических логарифмических уравнений Презентация на тему Этика государственного служащего, правила ношения формы
Презентация на тему Этика государственного служащего, правила ношения формы  В лабиринте тригонометрических формул
В лабиринте тригонометрических формул Презентация на тему Дельфин Физминутка для глаз
Презентация на тему Дельфин Физминутка для глаз  Тригонометрические уравнения Автор: Серебрянская Л. А.
Тригонометрические уравнения Автор: Серебрянская Л. А.  Формулы для решения квадратного уравнения
Формулы для решения квадратного уравнения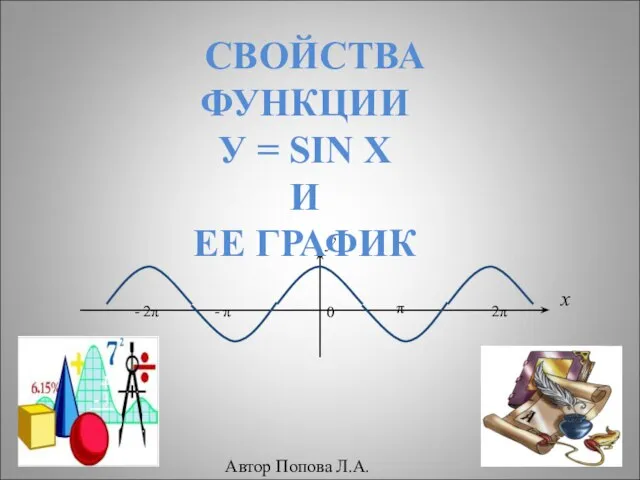 Свойства функции У = sin x и ее график
Свойства функции У = sin x и ее график Определение линейной функции
Определение линейной функции