Уравнение касательной к графику функции в точке

Лекция № 21
Уравнение касательной
к графику функции
в точке

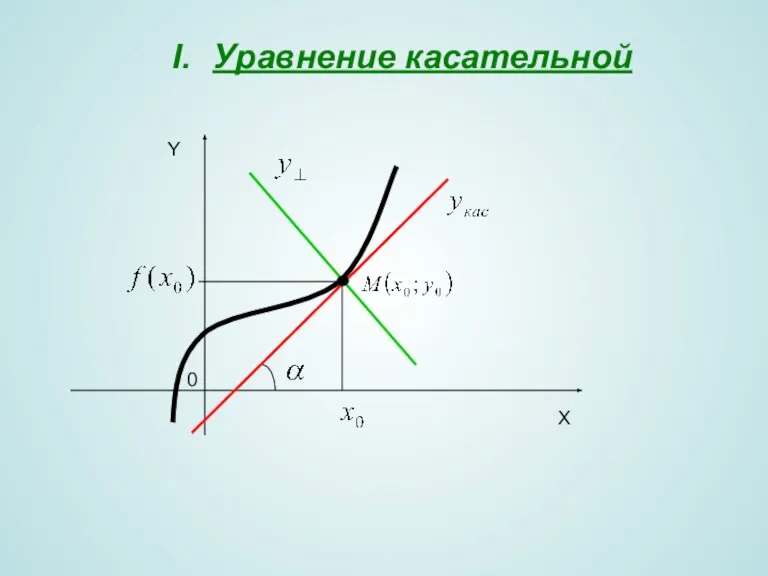
Уравнение касательной
X
Y
0

Пусть функция дифференцируема в точке . Прямая, определяемая уравнением
называется касательной к графику функции
в точке .

II. Уравнение нормали.
Прямая, перпендикулярная касательной в точке касания , называется нормалью к графику функции в этой точке.

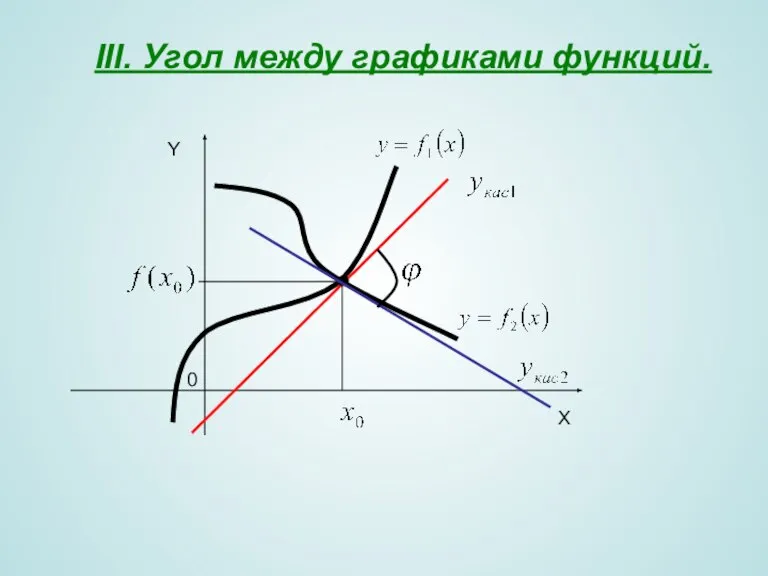
III. Угол между графиками функций.
X
Y
0

Под углом между графиками функций
и в их общей точке понимают угол между касательными к этим графикам в точке .
Если ,то и кривые пересекаются под прямым углом.