Можно найти по формуле
Физический смысл производной
В задаче о мгновенной скорости каждому t соответствует свое значение мгновенной скорости, т.е. производная от пути по времени есть скорость
В общем случае, производная – это скорость изменения функции.
Если функция f(x) имеет производную в точке x, то эта функция называется дифференцируемой в этой точке.
Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке.
Операция нахождения производной называется дифференцированием.
у
y=f(x)
x
h
Физический смысл производной
Производную сложной функции







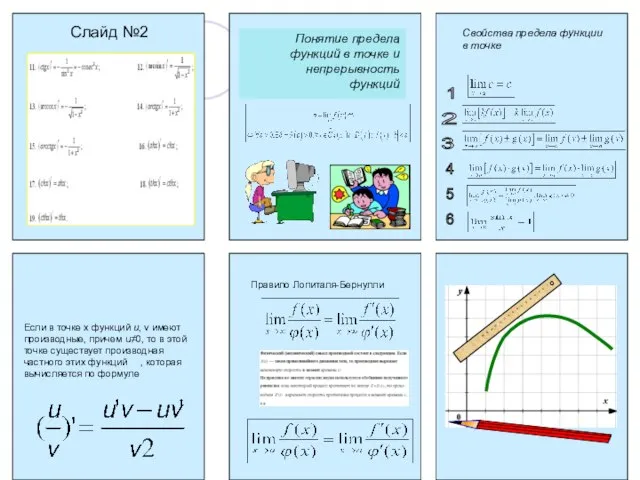

 Презентация на тему Движение Земли вокруг Солнца 2 класс
Презентация на тему Движение Земли вокруг Солнца 2 класс  Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»
Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»  Ещё раз о квадратных уравнениях
Ещё раз о квадратных уравнениях Решение линеиных неравенств
Решение линеиных неравенств Функции y=tg x и y=ctg x, их свойства и графики
Функции y=tg x и y=ctg x, их свойства и графики Metod-racionalizacii.pptx
Metod-racionalizacii.pptx Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Психические процессы
Презентация на тему Психические процессы  Теорема косинусов. Выполнили: Давыдова Катерина Орешенкова Дарья.
Теорема косинусов. Выполнили: Давыдова Катерина Орешенкова Дарья.  Презентация на тему Тест Мюнстерберга на восприятие и внимание
Презентация на тему Тест Мюнстерберга на восприятие и внимание  Вычисление площадей плоских фигур - презентация по Алгебре_
Вычисление площадей плоских фигур - презентация по Алгебре_ Pryamaya-proporcionalnost.ppt
Pryamaya-proporcionalnost.ppt Решение рациональных уравнений
Решение рациональных уравнений Прогрессия - движение вперёд !
Прогрессия - движение вперёд ! Презентация на тему Глубинная психология
Презентация на тему Глубинная психология  Презентация на тему Дельфин Физминутка для глаз
Презентация на тему Дельфин Физминутка для глаз  Применения матриц в экономике
Применения матриц в экономике Презентация на тему Советы родителям будущих первоклассников
Презентация на тему Советы родителям будущих первоклассников  Функции 7 класс
Функции 7 класс Свойства функции Алгебра 9 класс
Свойства функции Алгебра 9 класс  Координатная плоскость
Координатная плоскость 667
667 Темы: График квадратичной функции. Неравенства с одной переменной.
Темы: График квадратичной функции. Неравенства с одной переменной.  Презентация на тему Природа и общество в философии
Презентация на тему Природа и общество в философии Презентация на тему Программа менеджмента качества Э. Деминга
Презентация на тему Программа менеджмента качества Э. Деминга  Математика 5 класс
Математика 5 класс Целое уравнение и его корни Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год
Целое уравнение и его корни Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год  Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле